Теорема о сходимости и точности метода итераций

Теорема. Пусть уравнение 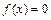приведено к виду 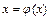таким образом, что функция 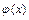дифференцируема и выполняется условие 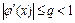для всех .

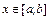Тогда:

· последовательность ;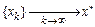

· ошибка .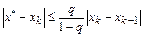

Доказательство. Построим два соседних приближения в методе итераций:

.

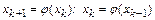Очевидно, что

,

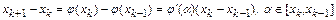или

.

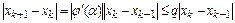Таким образом,

.

Запишем это неравенство для k= 1, 2 ,…,k в следующем виде:

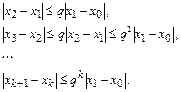(4.1)

Построим вспомогательный ряд

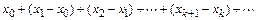(4.2)

Частичная сумма членов этого ряда 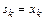, а значит 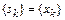. По этой причине

.

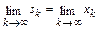Последовательность частичных сумм ряда (4.2) совпадает с последовательностью приближений, вычисленных по методу итераций, а доказательство сходимости вспомогательного ряда эквивалентно доказательству сходимости метода итераций.

Рассмотрим вспомогательный числовой ряд

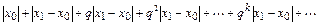(4.3)

Ряд (7.3) сходится абсолютно при 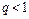. Но ряд (7.2) является мажорируемым к ряду (4.3) в силу неравенств (7.1). Следовательно, ряд (7.2) также сходится. Первая часть теоремы доказана.

Напоминание. Ряд называется мажорируемым, если каждый его член по модулю не превосходит соответствующего члена некоторого сходящегося ряда с положительными членами.

Получим теперь оценку погрешности приближенного решения. На основании леммы имеем:

.

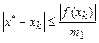Найдем 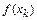. Так как , то

.

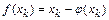Теперь вычислим . По определению

.

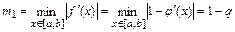Тогда

.

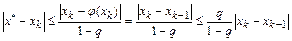Вторая часть теоремы также доказана.

Замечание 1. Величину 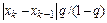можно использовать в качестве предельной абсолютной погрешности. Для ее расчета привлекаются два соседних приближения и минимальное по модулю значение первой производной. Предельная же абсолютная погрешность лежит в основе критерия завершения итерационного процесса. Критерий останова:

,

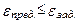где 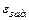– допустимая величина абсолютной ошибки, или

.

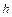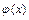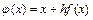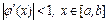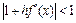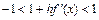Замечание 2. Рассмотрим теперь, как выбирается при построении функции . Напомним, что . Из теоремы следует, что для сходимости метода итераций необходимо, чтобы . Значит или для 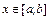. Отсюда можно сделать вывод, что

· при ;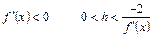

· при .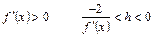

Лекция 6

Date: 2015-07-27; view: 642; Нарушение авторских прав