
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Инструменты управления качеством образовательного процесса
|
|
С точки зрения управления можно выделить два аспекта качества образовательного процесса: технический и функциональный.
Технический аспект применительно к образовательному процессу определяет его содержание, отвечает на вопрос что необходимо рассмотреть в рамках образовательной программы и устанавливает суть удовлетворяемой потребности. В основе содержания лежат рекомендации и положения образовательного стандарта, т.е. требования со стороны Федерального агентства по образованию.
Функциональный аспект определяет то, как удовлетворяется потребность. Применительно к образовательному процессу – это то, каким способом образовательная организация выполняет требования ФГОС.
Как в техническом, так и в функциональном аспекте важен уровень качества оказываемых образовательных услуг. Можно выделить четыре уровня качества образования:
Первый уровень – «Соответствие стандарту», или обеспечение нормативного качества. На этом уровне выясняются требования потребителей (государства, организации), утверждается стандарт, соответствующий запросам, отлаживаются процессы для обеспечения стандартного качества и осуществляются процедуры по его проверке.
Второй уровень – «соответствие использованию», или готовность образовательного учреждения соответствовать разнообразным запросам потребителя: общественных организаций, родителей, учеников. Маркетинговые исследования играют на этом уровне центральную роль. Чаще всего этот уровень означает переход на новую, более высокую ступень требований к качеству образовательных услуг.
Третий уровень – «соответствие фактическим требованиям рынка». Означает производство образовательных услуг высокого качества с одновременным снижением их себестоимости.
Четвертый уровень – «соответствие скрытым (неочевидным) потребностям рынка». Преимущество получает то образовательное учреждение, которое «просчитывает» скрытые потребности потребителей, использует инновационные и прорывные методики и технологии, заботится о повышении квалификации своих сотрудников.
Для того чтобы переходить с одного уровня на другой, т.е. повышать качество образовательного процесса можно использовать ряд инструментов, разработанных в системе менеджмента качества. Существуют следующие основные инструменты менеджмента качества:
– контрольный листок;
– расслаивание (стратификация);
– диаграмма причинно-следственных связей (Исикавы);
– диаграмма рассеивания;
– гистограмма;
– диаграмма Парето;
– контрольные карты Шухарта.
Контрольный листок. Представляет собой форму для регистрации и подсчета данных, собираемых в результате наблюдений или измерений контролируемых показателей в течение установленного периода времени. Собираемые данные могут быть как целочисленными (число пропусков занятий), так и интервальными (диапазон значений измерений).
Цель: сбор данных и их автоматическое упорядочение для облегчения дальнейшего использования собранной информации.
Суть: контрольный листок – это:
– средство регистрации данных, как правило, в виде бумажного бланка с заранее внесенными в него контролируемыми параметрами, соответственно которым можно заносить необходимые данные с помощью пометок или каких-либо символов;
– инструмент, позволяющий облегчить задачу контроля протекающих процессов и предоставить различного рода факты для анализа, корректировки и улучшения качества процессов.
Основное назначение контрольного листка – представлять информацию в удобном для восприятия виде. Контрольный листок позволяет распределить данные по категориям. Он показывает, как часто возникают те или иные события, поэтому информация контрольного листка является более систематизированной, чем обычный сбор данных. Ниже представлен пример контрольного листка по дисциплине (рис.1).
Контрольный листок (вариант 1)
Составил__________________Дата___________
Кафедра_________________________________________
Дисциплина «____________________________________»
| Учебный год | Успеваемость в % | ||
| 1 семестр | 2 семестр | 3 семестр | |
| 2012-2013 | |||
| 2013-2014 | |||
| 2014-2015 |
Рис. 1. Пример контрольной карты
Правила составления контрольных листков:
1. Определить события (несоответствия, проблемы процесса), которые необходимо регистрировать в контрольном листке.
2. Определить период сбора данных и подходящий интервал. Период сбора данных необходимо выбирать таким образом, чтобы он был репрезентативным, т.е. наиболее типичным для исследуемого процесса.
3. Определить категории данных для регистрации в контрольном листке – целочисленные данные или интервальные.
4. Разработать форму контрольного листка. В этой форме необходимо предусмотреть достаточно места для регистрации данных в течение всего установленного интервала времени. Форма должна содержать ясные формулировки категорий данных и разделы для суммарных данных по категориям и за весь интервал сбора данных.
5. Провести инструктаж сотрудников, ответственных за сбор информации. Каждый сотрудник должен понимать, как заполнять контрольный листок, какие события необходимо в нем регистрировать и в каком интервале времени.
6. Провести анализ данных и их дальнейшую обработку с помощью других инструментов качества.
Какая бы задача не стояла перед системой, объединяющей последовательность применения статистических методов, всегда начинают со сбора исходных данных, на базе которых затем применяют тот или иной инструмент. Для сбора исходных данных используют контрольные листки.
Расслаивание (стратификация). Стратификация или метод расслаивания статистических данных позволяет произвести отбор данных, отражающих требуемую информацию о процессе. В соответствии с этим методом данные делят на группы в соответствии с их особенностями.
Цель: контроль протекающих процессов и выявление проблем путем расслаивания (группировки) данных и обработки каждой группы в отдельности.
Суть: метод стратификации (расслаивания статистических данных) позволяет произвести селекцию данных, отражающую требуемую информацию о процессе, в соответствии с различными факторами.
При разделении данных на группы в соответствии с их особенностями группы именуют слоями (стратами), а сам процесс разделения – расслаиванием (стратификацией).
На практике метод стратификации используют многократно, расслаивая данные по различным признакам и анализируя возникающую при этом разницу.
Сбор данных следует вести с применением контрольных листков.
В производственных процессах используют метод называемый 5м: человек (man), машина (mashine), материал (material), метод (method), измерение (measurement).
В соответствии с этим расслаивание в рамках анализа образовательного процесса можно осуществлять следующим образом:
– по исполнителям – по квалификации, полу, стажу работы и т.п.;
– по оборудованию – по техническим средствам обучения, используемым программным средствам и т.д.;
– по материалу – по полу, по возрасту, по успеваемости, психологическим особенностям, количеству пропусков занятий и т.д.;
– по способу производства – по технологии, способам и методам обучения, месту обучения, форме обучения и т.д.;
– по измерению – по методу измерения, типу измерительных средств, их точности и т.д.
Например, данные, представленные в контрольном листке на рисунке 1 можно расслоить путем добавления графы посещаемость (см. рис. 2).
Контрольный листок (вариант 2)
Составил__________________Дата___________
Кафедра_________________________________________
Дисциплина «____________________________________»
| Учебный год | Успеваемость в % | |||||
| 1 семестр | 2 семестр | 3 семестр | ||||
| Успевае-мость | Количество пропусков | Успевае-мость | Количество пропусков | Успевае-мость | Количество пропусков | |
| 2012-2013 | ||||||
| 2013-2014 | ||||||
| 2014-2015 |
Рис.2. Пример контрольной карты
Такое расслаивание позволяет сделать более глубокий анализ, например, посмотреть зависит ли успеваемость от посещаемости, что показательно в анализе образовательного процесса вуза. Для расслаивания данных, представленных на рис.1 можно выбрать и другие факторы: состав группы, аудитория и т.д.
Диаграмма Исикавы – инструмент, обеспечивающий системный подход к определению фактических причин возникновения проблем. Эта диаграмма называется диаграммой причинно-следственных связей. Она помогает определить все факторы, влияющие на проблему или желаемый результат. Создание диаграммы лучше всего осуществлять во время мозговой атаки.
Цель – перечислить все факторы, влияющие на качество образовательного процесса, и составить схему взаимодействия между ними.
Суть: диаграмма позволяет в простой и доступной форме систематизировать все потенциальные причины рассматриваемых проблем, выделить из них самые существенные и провести поуровневый поиск первопричины.
Диаграмма Исикавы представляет собой структурную наглядную схему. Она иллюстрирует различные причины, их влияние на процесс, сортирует их и показывает их взаимосвязи. Для каждого следствия существует ряд причин. Нужно сгруппировать их по категориям. Этот прием необходим для определения возможных причин возникновения проблемы или выяснения факторов, ведущих к улучшению.
Общие правила построения диаграммы:
1. Прежде чем приступать к построению диаграммы, все участники должны придти к единому мнению относительно формулировки проблемы.
2. Изучаемая проблема записывается с правой стороны в середине чистого листа бумаги и заключается в рамку, к которой слева подходит основная горизонтальная стрелка – «хребет» (диаграмму Исикавы из-за своего внешнего вида часто называют «рыбьим скелетом»).
3. Наносятся главные причины (причины 1-го уровня), влияющие на проблему, – «большие кости». Они заключаются в рамки и соединяются наклонными стрелками с «хребтом».
4. Далее наносятся вторичные причины (причины 2-го уровня), которые влияют на главные причины («большие кости»), а те, в свою очередь, являются следствием вторичных причин. Вторичные причины записываются и располагаются в виде «средних костей», примыкающих к «большим». Причины 3-го уровня, которые влияют на причины 2-го уровня, располагаются в виде «мелких костей», примыкающих к «средним», и т. д. (Если на диаграмме приведены не все причины, то одна стрелка оставляется пустой).
5. При анализе должны выявляться и фиксироваться все факторы, даже те, которые кажутся незначительными, так как цель схемы – отыскать наиболее правильный путь и эффективный способ решения проблемы.
6. Причины (факторы) оцениваются и ранжируются по их значимости, выделяя особо важные, которые предположительно оказывают наибольшее влияние на показатель качества.
7. В диаграмму вносится вся необходимая информация: ее название; наименование дисциплины; имена участников; дата и т.д.
Каждая из линий, нанесенная на схему, должна представлять собой в зависимости от ее положения либо причину, либо следствие: предыдущая линия по отношению к последующей всегда выступает как причина, а последующая как следствие.
В общем случае существуют уже рассмотренные выше шесть возможных причин тех или иных результатов:
– материал (material),
– оборудование (machine),
– измерение (measurement),
– метод (method),
– люди (man),
– менеджмент (management).
На рис.3 приведен пример диаграммы Исикавы.

Рис. 3. Пример диаграммы Исикавы
Ценность такой диаграммы, безусловно, возрастает, если приведена не только группировка факторов, но их весовое значение, т.е. долю вклада каждого фактора и группы факторов в результат (показатель качества или проблему). Для этих целей мы предлагаем метод нормирования или последовательного сравнения [8], что подробно рассмотрено в практическом занятии 4.
Анализ причин и их весов приводит к пониманию сложившейся ситуации и определению первоочередных действий для улучшения качества анализируемого процесса, т.е. складывается план действий: причины, которые нужно устранить в первую очередь, во вторую и т.д.
Если система стабильна, то все факторы примерно в равной степени влияют на вариации результатов. Доля каждого фактора составляет примерно 1/7 ≈ 14%.
Появление среди этих факторов доминирующих причин нарушает стабильность системы, качество ухудшается, поведение системы становится непрогнозируемым, над ней теряется контроль. Очень важно, чтобы руководящие действия (менеджмент) не становились специальными причинами и не приводили к расшатыванию системы.
Диаграмма рассеяния. Диаграмма рассеяния показывает примерный характер взаимосвязи между числовыми характеристиками, соответствующими какой-либо паре факторов.
Цель: выяснение существования зависимости и выявление характера связи между двумя различными параметрами процесса.
Суть: диаграмма рассеяния – инструмент, позволяющий определить вид и тесноту связи между парами соответствующих переменных.
Эти две переменные могут относиться к:
– характеристике качества и влияющему на нее фактору;
– двум различным характеристикам качества;
– двум факторам, влияющим на одну характеристику качества.
Диаграмма рассеяния (точечная диаграмма) – математическая диаграмма, изображающая значения двух переменных в виде точек на декартовой плоскости. На такой диаграмме производится визуальный анализ объектов исследования с учетом по форме связи («облака» точек) и по наличию выбросов на диаграмме рассеяния. «Выбросы» – крайние значения признаков, не характерные для данной выборки, слишком большие или слишком малые значении, аномальные, при удалении которых связь полностью может измениться.
Варианты скоплений точек показаны на рис. 4:
а) пример абсолютной отрицательной корреляции;
б) сильной положительной корреляции;
в) взаимосвязь между значениями не усматривается;
г) взаимосвязь наличествует, но это не линейная зависимость, а параболическая.
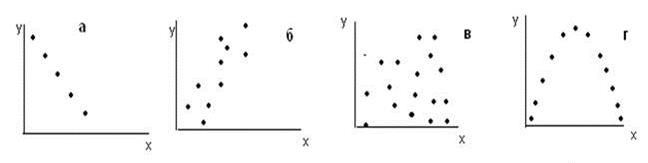
Рис. 4. Варианты скоплений точек на диаграммах рассеяния
Диаграмма рассеяния в процессе контроля качества используется также для выявления причинно-следственных связей показателей качества и влияющих факторов. Однако, стоит иметь ввиду, что наличие корреляции не является доказательством причинно-следственной связи признаков. Наличие корреляции свидетельствует о том, что, либо одно явление является частичной причиной другого, либо оба явления – следствие общих причин.
В качестве дополнения на построенные диаграммы часто добавляют линию тренда, подобранную по форме расположения точек (например, линейную, экспоненциальную и др), а также R-квадрат. R-квадрат – это коэффициент достоверности аппроксимации. Если R-квадрат > 0,8, говорят о высокой точности аппроксимации (модель хорошо описывает явление). Если R-квадрат лежит в диапазоне от 0,6 до 0,8, говорят об удовлетворительной аппроксимации (модель в целом адекватна описываемому явлению). Если R-квадрат < 0,6, принято считать, что точность аппроксимации недостаточна.
Рассмотрим пример. Преподавателю необходимо проанализировать влияние числа аудиторных контрольных работ на результат итоговой успеваемости.
Для решения данной задачи сначала заполняется листок регистрации на основании имеющихся данных (табл.1).
Таблица 1
Данные по качественной успеваемости
| Номер группы | Качественная успеваемость | ||||
| А | |||||
| В | |||||
| С | |||||
| Количество аудиторных контрольных работ |
В данном случае представление данных, оформленных в виде листка регистрации, позволяет сделать определенные выводы, однако не позволяет увидеть сложившуюся картину в целом. Поэтому следует построить диаграмму рассеяния (рис. 5).
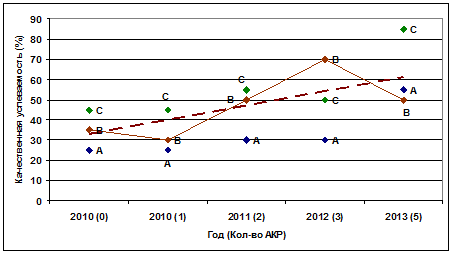
Рис. 5. Диаграмма рассеяния по качественной успеваемости и количеству АКР
Из диаграммы видно, что наблюдается общее статистическое повышение успеваемости с увеличением аудиторных контрольных работ, несмотря на отдельные колебания по группам.
Правила построения диаграммы рассеяния:
1. Определить, между какими парами данных необходимо установить наличие и характер связи. Желательно не менее 25-30 пар данных.
2. Для сбора данных подготовить бланк таблицы (листок регистрации), предусмотрев в нем графы для порядкового номера наблюдения i; независимой переменной характеристики, называемой аргументом х; зависимой переменной, называемой функцией (откликом) у.
3. По результатам наблюдения заполнить листок регистрации данных.
4. Нанести на диаграмму все необходимые обозначения. Данные, отраженные на диаграмме, должны быть понятны любому человеку, а не только тому, кто делал диаграмму.
Примечание. При наличии корреляционной зависимости можно осуществить контроль только одной (любой) из двух характеристик. При этом характер корреляционной зависимости, который определяется видом диаграммы рассеяния, дает представление о том, каким изменениям будет подвержен один из параметров при определенных изменениях другого. Так, в случае прямой корреляции при увеличении х на диаграмме у также будет увеличиваться.
В этом случае при осуществлении контроля причинных факторов x (откликов) характеристика у (функция) будет оставаться стабильной.
Гистограмма – один из вариантов столбиковой диаграммы, позволяющий зрительно оценить распределение статистических данных, сгруппированных по частоте попадания в определенный (заранее заданный) интервал.
Цель: контроль действующего процесса и выявление проблем, подлежащих первоочередному решению.
Суть: один из наиболее распространенных методов, помогающих интерпретировать данные по исследуемой проблеме.
Благодаря графическому представлению имеющейся количественной информации, можно увидеть закономерности, трудно различимые в простой таблице с набором цифр, оценить проблемы и найти пути их решения.
Порядок построения гистограммы:
1. Собрать данные, выявить максимальное и минимальное значения и определить диапазон (размах) гистограммы.
2. Полученный диапазон разделить на интервалы, предварительно определив их число (обычно 5 – 20 в зависимости от числа показателей), и определить ширину интервала.
3. Все данные распределить по интервалам в порядке возрастания: левая граница первого интервала должна быть меньше наименьшего из имеющихся значений.
4. Подсчитать частоту каждого интервала.
5. Вычислить относительную частоту попадания данных в каждый из интервалов.
6. По полученным данным построить гистограмму – столбчатую диаграмму, высота столбиков которой соответствует частоте или относительной частоте попадания данных в каждый из интервалов:
– наносится горизонтальная ось, выбирается масштаб и откладываются соответствующие интервалы;
– затем строится вертикальная ось, на которой также выбирается масштаб в соответствии с максимальным значением частот.
В классическом варианте гистограмма используется для определения проблем при помощи анализа формы разброса значений, центрального значения, его близости к номиналу, характера рассеивания (см. рис. 6)
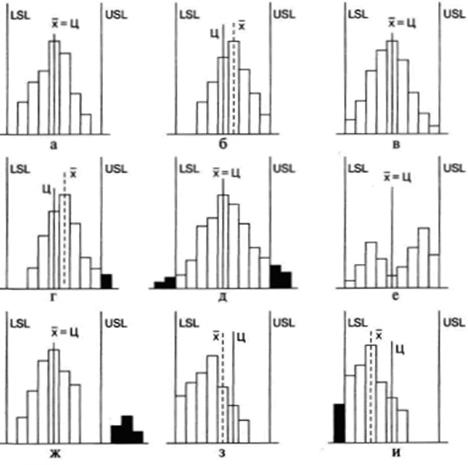
Рис. 6. Варианты расположения гистограммы по отношению к технологическому допуску
Приведем краткие описания ситуаций, представленных на рис. 6 в соответствии с [7]:
а) всё хорошо: среднее совпадает с номиналом, вариабельность в пределах допусков;
б) следует сместить среднее для совпадения с номиналом;
в) следует уменьшить рассеивание;
г) следует сместить среднее и уменьшить рассеивание;
д) следует значительно уменьшить рассеивание;
е) смешаны два ряда данных; следует разбить на две гистограммы, и проанализировать их;
ж) аналогично предыдущему пункту, только ситуация более критичная;
з) необходимо понять причины такого распределения; «обрывистый» левый край, говорит о каких-то действиях в отношении исследуемой совокупности;
и) аналогично предыдущему.
Рассмотрим пример: необходимо провести анализ того, настолько объективно были оценены выпускники во время итоговой аттестации. Для решения задачи построим гистограмму распределения среднего балла выпускников. Диапазон результатов от 3 до 5. Количество выпускников – 100 человек. Разобьем диапазон на 8 интервалов. Полученные в результате данные представим в виде таблицы (табл. 2).
Таблица 2
Результаты итоговой аттестации
| Интервалы | 3,0-3,25 | 3,26-3,5 | 3,51-3,75 | 3,76-4,0 | 4,01-4,25 | 4,26-4,5 | 4,51-4,75 | 4,76-5,0 |
| Количество выпускников |
По данным, представленным в таблице, построим гистограмму.
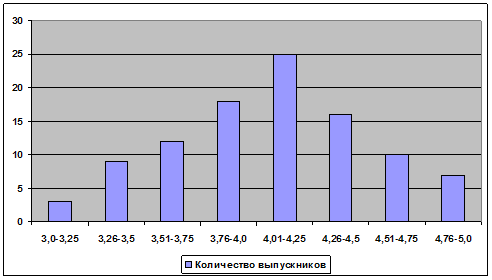
Рис. 7. Гистограмма по результатам итоговой аттестации
Анализ гистограммы показывает, что поскольку она близка к нормальному распределению, оценки выпускников выставлены абсолютно объективно. Однако, поскольку гистограмма несколько смещена вправо относительно центра, можно сделать вывод о том, что либо группа в целом сильная, либо требования в целом несколько занижены. Для выяснения этого обстоятельства необходимо использовать другие инструменты качества.
Диаграмма Парето. Диаграмма Парето – это столбчатая диаграмма, на которой интервалы (столбики) упорядочены по убыванию. На такой диаграмме интервалы могут представлять виды дефектов, их локализацию, ошибки и т.д. Высота интервалов (высота столбиков) показывает частоту возникновения дефектов, их процентное соотношение, стоимость, время и т.д.
Диаграмма Парето является графическим отображением правила Парето. В менеджменте качества применение этого правила показывает, что значительное число несоответствий и дефектов возникает из-за ограниченного числа причин. Коротко правило Парето формулируется так: 20% причин создают 80% проблем, поэтому надо найти эти причины. Данный подход позволяет рационально распределить силы и ресурсы.
Цель: выявление проблем, подлежащих первоочередному решению.
Суть: диаграмма Парето является инструментом, позволяющим выявить и отобразить проблемы, установить основные факторы, с которых нужно начинать действовать, и распределить усилия с целью эффективного разрешения этих проблем.
Различают два вида диаграмм Парето:
– по результатам деятельности, которая предназначена для выявления главной проблемы нежелательных результатов деятельности;
– по причинам, которая используется для выявления главной причины проблем, возникающих в ходе деятельности.
Таким образом, использование диаграммы Парето позволяет установить приоритет действиям, необходимым для решения проблемы. Кроме того, диаграмма Парето и правило Парето позволяют отделить важные факторы от малозначимых и несущественных.
Общие правила построения диаграммы Парето:
1. Решить, какие проблемы (причины проблем) надлежит исследовать, какие данные собирать и как их классифицировать.
2. Разработать формы для регистрации исходных данных.
3. Собрать данные, заполнив формы, и подсчитать итоги по каждому исследуемому фактору (показателю, признаку).
4. Для построения диаграммы Парето подготовить бланк таблицы, предусмотрев в нем графы для итогов по каждому проверяемому фактору в отдельности, накопленной суммы числа появлений соответствующего фактора, процентов к общему итогу и накопленных процентов.
5. Заполнить таблицу, расположив данные, полученные по проверяемому фактору, в порядке убывания значимости.
6. Подготовить оси (одну горизонтальную и две вертикальные линии) для построения диаграммы.
Нанести на левую ось ординат шкалу с интервалами от 0 до общей суммы количества выявленных факторов, а на правую ось ординат – шкалу с интервалами от 0 до 100, отражающую процентную меру фактора.
Разделить ось абсцисс на интервалы в соответствии с числом исследуемых факторов или относительной частотой.
7. Построить столбиковую диаграмму. Высота столбца (откладывается по левой шкале) равна числу появлений соответствующего фактора. Столбцы располагают в порядке убывания (уменьшения значимости фактора). Последний столбец характеризует «прочие», то есть малозначимые факторы, и может быть выше соседних.
8. Начертить кумулятивную кривую (кривую Парето) – ломаную, соединяющую точки накопленных сумм (количественной меры факторов или процентов). Каждую точку ставят над соответствующим столбцом столбиковой диаграммы, ориентируясь на его правую сторону.
9. Нанести на диаграмму все обозначения и надписи.
10. Провести анализ диаграммы Парето.
Рассмотрим пример применения диаграммы Парето. Группа экспертов вуза независимо отвечала на вопрос ректора: «Каковы возможные пути улучшения качества выпускников?».
Экспертов было 25 человек. В результате было подано 70 предложений, некоторые из которых повторялись.
Всего было названо 8 направлений для улучшения качества выпускников, причем, было подсчитано, сколько раз повторялось каждое предложение. Полученные данные были представлены в виде таблицы (табл. 3).
Таблица 3
Результаты опроса
| Предложения экспертов | Количество повторений предложения |
| 1…… | |
| 2…… | |
| 3…… | |
| 4…… | |
| 5…… | |
| 6…… | |
| 7…… | |
| 8…… | |
| Всего | 70 предложений |
По данным, представленным в табл.2 построили гистограмму, которая графически отображает полученные результаты (рис. 8).
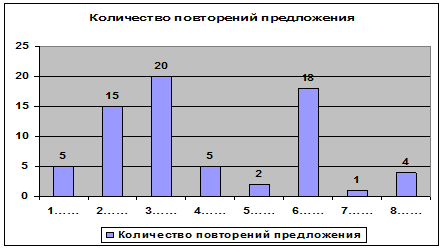
Рис. 8. Гистограмма по результатам опроса
Для построения диаграммы Парето данные в таблице сортируются по количеству повторений предложений, рассчитывается доля каждого предложения в общем количестве (в процентах) и суммарное воздействие как текущее, которое суммируется со всеми предыдущими. Полученные данные представлены в таблице (табл. 3).
Таблица 3
Исходные данные для диаграммы Парето
| Предложения экспертов | Количество повторений предложения | Доля каждого предложения | Суммарное воздействие |
| 28,57% | 28,00% | ||
| 25,71% | 54,29% | ||
| 21,43% | 75,71% | ||
| 7,14% | 82,86% | ||
| 7,14% | 90,00% | ||
| 5,71% | 95,71% | ||
| 2,86% | 98,57% | ||
| 1,43% | 100,00% | ||
| Всего | 100,00% |
На основе полученных данных строим диаграмму Парето (рис. 9).
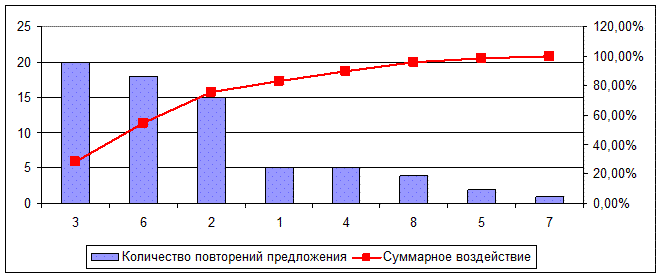
Рис. 9. Диаграмма Парето по результатам опроса
Диаграмма показывает, что наиболее значимыми являются причина 3, причина 6 и причина 2. Эти предложения по улучшению качества подготовки выпускников необходимо реализовать в первую очередь. Частичное влияние оказывает и причина 1. Все остальные причины никакой роли в улучшении процесса не играют.
Карта Шухарта. Контрольная карта Шухарта – это графическое средство принятия решений относительно стабильности или предсказуемости любого процесса. Этот инструмент позволяет определить способы управления соответствующим процессом.
Цель: осуществлять оценку управляемости действующего процесса. В случае управляемости – оценку его воспроизводимости. В случае статистически неуправляемого процесса провести корректирующее воздействие и проверку эффективности принятых мер.
Суть: контрольные карты (КК) является инструментом, позволяющим отслеживать ход процесса и воздействовать на него (с помощью соответствующей обратной связи), предупреждая его отклонения от предъявляемых к процессу требований.
Контрольные карты Шухарта принято делить на две группы: по качественным (годен – негоден) и количественным признакам.
Теория контрольных карт различает два вида изменчивости.
Первый вид – случайная изменчивость, вызываемая «общими» или «случайными» причинами. Она обусловлена широким набором таких причин, которые присутствуют постоянно. Эти причины нелегко или экономически нецелесообразно в данный момент выявлять, и среди них нет заметно преобладающих. Однако в целом сумма всех этих причин создает то, что можно считать системной изменчивостью (вариабельностью) процесса. Предотвращение или уменьшение влияния обычных причин требует управленческих решений, направленных в первую очередь на изменение системы.
Второй вид изменчивости представляет собой случайные вмешательства в процесс таких причин, какие не свойственны процессу внутренне, не принадлежат системе и могут быть обнаружены и устранены, по крайней мере, теоретически. Эти причины принято называть «специальными» или «особыми» причинами вариабельности. К ним, например, могут быть отнесены срыв занятий, ошибки персонала, невыполнение процедур, и т.д.
До тех пор, пока в процессе присутствуют специальные причины вариаций, он, по определению, предложенному Шухартом, является нестабильным, или неуправляемым.
Поэтому целью контрольных карт является определение того, насколько стабилен процесс и стабилен ли он вообще. Если нет, то главная задача – приведение процесса в стабильное состояние, для чего нужно найти главные причины вмешательства в систему и устранить их. Если в процессе присутствуют только общие причины вариабельности, то он находится в статистически управляемом состоянии. Важно иметь в виду, что границы контрольных карт Шухарта рассчитываются по данным о самом процессе, не имеют отношения к допускам, и не являются линиями каких-либо вероятностей.
Применение контрольных карт для отображения изменений показателей во времени дает возможность точно определить, когда и как изменился процесс и тем самым обеспечить базу для управления им. Например, если контрольная карта отображает единичный случай выхода показателя за контрольные границы, то нет необходимости предпринимать какие-либо действия по корректировке процесса. Если же, например, контрольная карта показывает асимметричное смещение контролируемого показателя (в течение длительного интервала времени) относительно линии средних значений, то процесс требует вмешательства и принятия корректирующих действий.
Для управления процессами разработаны и применяются различные контрольные карты. Например, существуют такие контрольные карты: средних значений, медиан, средних квадратических отклонений, размахов, числа дефектных единиц продукции, доли дефектных единиц продукции, числа дефектов, числа дефектов на единицу продукции и другие. Их выбор зависит от целей управления и вида контролируемых данных (количественный признак или альтернативный признак). Если необходимо определять фактические значения контролируемого параметра, то такой вид контроля называется контролем по количественному признаку. Если нет необходимости знать фактическое значение контролируемого параметра, а просто достаточно установить соответствие или несоответствие этого параметра установленным требованиям, то такой вид контроля называется контролем по альтернативному признаку. Исходя из этих условий, выбираются соответствующие контрольные карты.
Точки, которые наносятся на контрольные карты, могут быть как результатом прямых измерений отдельного показателя процесса, так и суммарным (комплексным) значением группы показателей, полученных в один момент времени. Комплексный показатель может включать, например, среднее значение по группе измерений, среднее значение отклонений, процент дефектов, среднее число дефектов на единицу и т.п.
Контрольные границы определяют предел ожидаемых изменений процесса, когда действуют только наиболее типичные для этого процесса факторы. Наносятся контрольные границы, как правило, на расстоянии трех стандартных отклонений случайной величины от линии средних значений.
Правила построения контрольных карт:
При построении контрольных карт на оси ординат откладываются значения контролируемого параметра, а на оси абсцисс – время t взятия выборки (или ее номер).
Контрольная карта состоит обычно из трех линий. Центральная линия представляет (ЦЛ) собой эталонное значение характеристики. Для оценки того, находится ли процесс в статистическом управляемом состоянии, эталонным обычно служит арифметическое значение (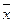 ) рассматриваемых данных.
) рассматриваемых данных.
Две другие линии, одна из которых находится над центральной – верхний контрольный предел (ВКП), а другая под ней – нижний контрольный предел (НКП), представляют собой максимально допустимые пределы изменения значений контролируемой характеристики (показателя качества).
Контрольные границы находятся на расстоянии 3σ от центральной линии, где σ – внутригрупповое стандартное отклонение (используемой статистики). Границы 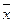 ±3σ указывают, что около 99,7% значений характеристик подгрупп попадают в эти пределы при условии, что процесс находится в статистически управляемом состоянии. Другими словами, есть риск равный 0,3%, что нанесенная точка окажется вне контрольных границ, когда процесс стабилен. В результате неправильно решают, что процесс вышел из состояния статистической управляемости, и делают попытку выявления несуществующей проблемы. В этом случае говорят об ошибке первого рода. Контрольные границы иногда называют «границы действий». Попадание точки вне эти границы считается сигналом к действию.
±3σ указывают, что около 99,7% значений характеристик подгрупп попадают в эти пределы при условии, что процесс находится в статистически управляемом состоянии. Другими словами, есть риск равный 0,3%, что нанесенная точка окажется вне контрольных границ, когда процесс стабилен. В результате неправильно решают, что процесс вышел из состояния статистической управляемости, и делают попытку выявления несуществующей проблемы. В этом случае говорят об ошибке первого рода. Контрольные границы иногда называют «границы действий». Попадание точки вне эти границы считается сигналом к действию.
В дополнении к трем основным на контрольной карте иногда проводят ещё границы на расстоянии 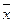 ±2σ. Любое выборочное значение, попадающее за эти границы, служит предостережением о грозящей ситуации выхода процесса из состояния статистической управляемости. Эти границы иногда называют «предупреждающими».
±2σ. Любое выборочное значение, попадающее за эти границы, служит предостережением о грозящей ситуации выхода процесса из состояния статистической управляемости. Эти границы иногда называют «предупреждающими».
Отметим, что в каждом конкретном случае имеет смысл обращать внимание и на нормативно заданные границы исследуемого процесса или его результатов, а не только на статистически заданные границы варьирования (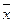 ±2σ или
±2σ или 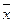 ±3σ). Кроме того, внимание должно быть уделено и смещению средней линии при сопоставлении двух и более карт Шухарта одного и того же процесса, например, за разные периоды наблюдений.
±3σ). Кроме того, внимание должно быть уделено и смещению средней линии при сопоставлении двух и более карт Шухарта одного и того же процесса, например, за разные периоды наблюдений.
Более глубоко вопросы использования данного инструмента качества можно изучить в ГОСТ 50779.42-99, в котором изложен подход к статистическому управлению. Подбор статистик для разных исходных данных можно осуществить в соответствии с материалом приложения настоящего учебного пособия.
Рассмотрим пример использования контрольных карт Шухарта. При анализе результатов курсового проектирования преподаватель провел статистические исследования – он определил выборку – по 5 проектов из каждой группы (n=5=const), при этом фиксировал типовые ошибки (дефекты). Данные по 7 группам были сведены в таблицу (табл.4).
Таблица 4
Данные по числу ошибок в курсовых проектах разных групп
| № групп | |||||||
| Число типовых ошибок |
Так как мы имеем дело с качественными признаками (типами ошибок), воспользуемся следующими расчетами:
Среднее число дефектов в выборке: 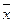 = Σс / 7=31/7=4,42.
= Σс / 7=31/7=4,42.
Отклонение: σ=√ 4,42 =2,1
Верхнее предельное отклонение: В.О. =4,42 + 3σ=10,72.
Нижнее предельное отклонение: Н.О. =4,42 - 3σ=0.
Построим контрольную карту (рис. 10).
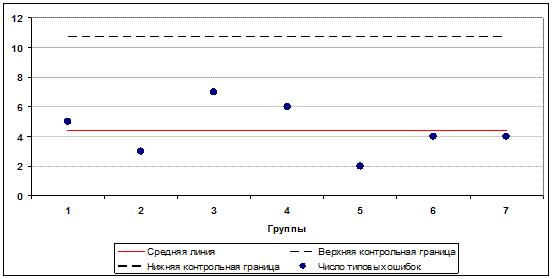
Рис. 10. Карта Шухарта по числу ошибок в курсовых проектах
Анализ карты показывает, что процесс стабильный. Однако среднее число дефектов 4,42 на проект не устраивает кафедру. Для улучшения процесса необходим анализ с помощью диаграммы Парето, который позволит выявить и устранить наиболее типичные ошибки.
Рассмотрим еще один пример. Предположим, что было проведено анкетирование по оценке удовлетворенности студентов преподаванием дисциплин.
Для анализа выбрали 10 дисциплин. Анализ проводили в трех группах по 20 человек.
По окончании анкетирования были получены следующие результаты (см. табл. 5).
Таблица 5
Данные опроса по удовлетворенности студентов преподаванием дисциплин
| Уровни | 1-я дисциплина | 2-я дисциплина | … | 10-я дисциплина |
| Удовлетворен | ||||
| Частично удовлетворен | ||||
| Не удовлетворен |
Расчет границ контрольной карты удовлетворенности, проводится аналогично предыдущему примеру, так как данные измерены в порядковой шкале.
Итак:
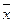 = 40,6
= 40,6
σ = √ 40,6 = 6,37
В.О. = 40,6 + 3х6,37=59,7
Н. О. = 40,6 – 3х6,37=21,5
На основании расчета была построена карта Шухарта.
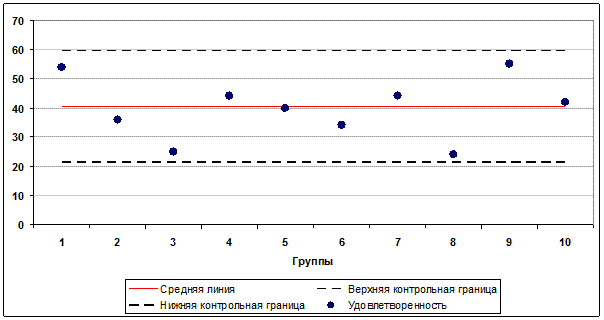
Рис. 11. Карта Шухарта для оценки удовлетворенности студентов по результатам опроса
В двух группах 3 и 8 значения удовлетворенности приближаются к нижнему пограничному значению. Причины низкой удовлетворенности можно установить, используя другие инструменты качества, например диаграммы Исикавы.
Пример построения карт Шухарта на основе и количественных данных будет рассмотрен в практической части настоящего пособия.
Добиться улучшения путем корректировки и исправления результатов невозможно. В этом случае необходимо заниматься совершенствованием системы в целом. Попытки исправить худшие результаты или добиться исключительно лучших результатов приведут к потере стабильности процессов и, как следствие, к ухудшению качества и росту издержек.
Основной путь улучшений заключается в совершенствовании всей системы образовательной организации за счет эффективного менеджмента, понимающего статистическую природу происходящих процессов, постоянно изучающего и анализирующего статистические данные о процессах и системе в целом для принятия обоснованных решений, имеющих минимальные отрицательные последствия.
Статистический подход к менеджменту представляет собой деятельность по управлению процессами, при которой акцент делается на уменьшение отклонений характеристик процесса от намеченных целей. Стабильность процессов – это суть менеджмента, нацеленного на постоянное улучшение и использующего для этого статистический подход.
Если руководитель вмешивается в процесс без проведения статистического изучения, анализа процесса и статистического понимания направлений его улучшения, то оно будет терять свою способность контролировать ход процесса и управлять им. Неумелое руководство и жажда быстрых результатов в итоге приведут к хаосу.
Таким образом, улучшения результатов и достижения намеченных целей можно добиться только совершенствованием образовательной системы в целом.
Помимо рассмотренного выше инструментария в контексте улучшения качества образования несомненный интерес представляет создание системы качества оценивания результатов обучения.
Date: 2015-07-27; view: 9610; Нарушение авторских прав