
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Пример 4. Расчет рабочего армирования монолитных несущих ригелей перекрытия с учетом действия в них продольного реактивно распора
|
|
Расчет рабочего армирования монолитных несущих ригелей перекрытия с учетом действия в них продольного реактивно распора.
Трехпролетные неразрезные несущие ригеля выполнены с длиной пролетов по осям колонн 3l2 = 3x6.20 м, размеры сетки колонн по осям 6.20х6.20 м. Ширина стенки монолитного таврового несущего ригеля bw1 = 0.40м, полная высота сечения h = 0.26 м, рабочая высота сечения h0 = 0.23м. Высота сечения многопустотных плит h = 0.22 м. Потолки плоские. Глубина размещения монолитных шпонок в полостях по торцам плит 0.1м. Расчетная ширина сечения несущего крайнего ригеля bw = 0.5 м, среднего – bw = 0.6 м. Высота поперечного сечения связевых ригелей 0.22 м, а ширина – 0,50 м. Сечение железобетонных колонн 0.4 x 0.4 м, высота этажа hfl = 3.0 м.
Бетон всех конструктивных элементов класса В25 (Rb = 14.5 МПа, Rbt = 1.05 МПа), рабочая арматура класса Ат500с (Rs = 450 МПа, Rsс = 400 МПа). Полная вертикальная расчетная нагрузка для I группы предельных состояний (по прочности) составляет g = 8.4 кПа, в т.ч. постоянная и длительная gd = 6.40 кПа.
Расчет
1. Продольный реактивный распор определяется:
- в крайних пролетах несущих ригелей по величине части временной нагрузки, составляющей разницу временной вертикальной нагрузки на соседние по высоте перекрытия многоэтажного здания, определяемую величиной снижения временной вертикальной нагрузки на перекрытие многоэтажного здания коэффициентом сочетаний ψAr определяемом согласно п.3.8 СНиП 2.01.07-85
- в средних пролетах несущих ригелей по полной величине расчетной вертикальной нагрузки на перекрытие за вычетом постоянной и длительной.
Грузовая площадь для нагрузки, приходящейся в крайнем пролете на средний несущий ригель, составляет Ac = l2xl1 = 6.2 x 6.2 = 38.4 м2, для крайнего (бортового) несущего ригеля в том же пролете Ak = 0.5×Ac = 19.2 м2.
Величина снижения временной нагрузки определяется по величине коэффициента сочетаний ψA (п.3.8 СНиП 2.01.07-85) для среднего ригеля:
ψA1c = 0.4 + = 0.4 + = 0.69;
для крайнего ригеля:
ψA1k = 0.4 + = 0.81;
Пониженное значение полной вертикальной расчетной нагрузки на перекрытие в крайних пролетах несущего ригеля составляет:
для среднего ригеля gc’ = 6.4 + 0.69×1.5×1.3 = 7.5 кПа;
для крайнего ригеля gk’ = 6.4 + 0.81×1.5×1.3 = 8.0 кПа.
2. Значение изгибающего момента от действия расчетной нагрузки в расчетных сечениях несущих ригелей, определены упругим расчетом каркаса здания МКЭ (ППП “Stark-ES”) и представлены в таблице 1.
3. Площадь сечения рабочей арматуры класса А500с, предельная высота сжатой зоны и предельное усилие в расчетных сечениях, несущих ригелей, рассчитанные в соответствии со СНиП 2.01.03-84* по величине усилий от полной расчетной нагрузки, представленных в табл. 1, приведены в табл. 2.
Таблица 1
| Пролеты | Расположение расчетного сечения | Несущий ригель | Нагрузка | Обозначение усилия | Величина изгибаемого момента, кНм |
| крайний пролет | Середина пролета | крайний | полная | ML1 | 51.6 |
| пониж., полная | ML1' | 49.0 | |||
| постоянная | MLd1 | 39.3 | |||
| средний | полная | ML2 | 79.2 | ||
| пониж., полная | ML2' | 70.6 | |||
| постоянная | MLd2 | 60.3 | |||
| У крайней колонны | крайний | полная | M01k | -68.2 | |
| пониж., полная | M0'1k | -64.5 | |||
| постоянная | M0d1k | -52.0 | |||
| средний | полная | M02k’ | -108.3 | ||
| пониж., полная | M02k | -96.3 | |||
| постоянная | M0d2k | -82.5 | |||
| У средней колонны | крайний | полная | M01 | -76.6 | |
| пониж., полная | M'01 | -72.2 | |||
| постоянная | M0d1 | -58.4 | |||
| средний | полная | M02 | -117.1 | ||
| пониж., полная | M'02 | -104.5 | |||
| постоянная | M0d2 | -89.2 | |||
| средний пролет | У колонны | крайний | полная | M012 | -76.6 |
| постоянная | M0d12 | -58.4 | |||
| средний | полная | M022 | -117.1 | ||
| постоянная | M0d22 | -89.2 | |||
| В середине пролета | крайний | полная | ML21 | 48.4 | |
| постоянная | MLd21 | 36.9 | |||
| средний | полная | ML22 | 73.8 | ||
| постоянная | MLd22 | 56.2 |
Таблица 2
| Пролеты | Расположение расчетного сечения | Несущий ригель | Принятое сечение рабочей арматуры, м2 | Высота сжатой зоны Xu, м | Предельный момент Mu в расчетном сечении, кНм |
| крайний пролет | Середина пролета | крайний ригель | 5х12A500c | 3.5х10-2 | 54.0 |
| As = 5.65х10-4 | |||||
| средний ригель | 2х20+2х2 | 4.4х10-2 | 79.9 | ||
| As = 8.54х10-4 | |||||
| У крайней колонны | крайний ригель | 2х20+1х2 | 4.6х10-2 | 69.0 | |
| As = 7.41х10-4 | |||||
| средний ригель | 2х25+3х2 | 6.8х10-2 | 116.4 | ||
| As = 1.32х10-3 | |||||
| У средней колонны | крайний ригель | 2х20+2х2 | 5.3х10-2 | 78.2 | |
| As = 8.54х10-4 | |||||
| средний ригель | 3х25+2х2 | 8.8х10-2 | 142.2 | ||
| As = 1.70х10-3 | |||||
| средний пролет | У колонны | крайний ригель | 2х20+2х2 | 5.3х10-2 | 78.2 |
| As = 8.54х10-4 | |||||
| средний ригель | 3х25+2х2 | 8.8х10-2 | 144.2 | ||
| As = 1.70х10-3 | |||||
| В середине пролета | крайний ригель | 5х2 | 3.5х10-2 | 54.0 | |
| As = 5.65х10-4 | |||||
| средний ригель | 2х20+2х2 | 4.4х10-2 | 79.9 | ||
| As = 8.54х10-4 |
4. Значение момента Mcrс, вызывающего образование вертикальных трещин в поперечных сечениях ригелей, определяется:
Mcrc = b1×Rbt×b×h2/3.5
Коэффициент b1 = 1.10 для крайнего ригеля и 1.15 — для среднего, учитывающий включение в работу примыкающих многопустотных плит.
Величина Mcrc:
– для крайнего ригеля
Mcrc = 1.10×1050×0.50×0.262/3.5 = 11.2 кНм;
– для среднего ригеля
Mcrc = 1.15×1050×0.60×0.262/3.5 = 14.0 кНм;
5. Величина высоты "u" развития вертикальных трещин в расчетных сечениях ригелей при величинах характерных расчетных нагрузок, представленных в табл. 1,определяется:
 ,
,
где: M – величина изгибающего момента в расчетном сечении ригеля для рассматриваемого уровня нагрузки, 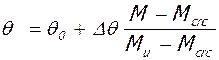 - коэффициент, учитывающий достигнутый уровень напряжений в рабочей арматуре для рассматриваемого уровня нагрузки;
- коэффициент, учитывающий достигнутый уровень напряжений в рабочей арматуре для рассматриваемого уровня нагрузки; 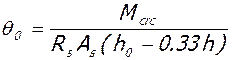 ;
;
Δ 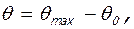
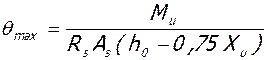 ;
;
Rs и As - расчетное сопротивление растяжению и площадь сечения рабочей арматуры ригеля, h и h0 – соответственно полная и рабочая высота сечения ригеля; Mu, Xu и Mcrc - определены выше (табл.2 и п.4).
5.1. Высота u трещины в середине крайнего пролета крайнего ригеля:
- при полной нагрузке:
M = Mu = 51,6 кНм, Mu = 54,0 кНм, Xu = 3,5·10-2 м, As = 5,65·10-4 м2.
 ;
;
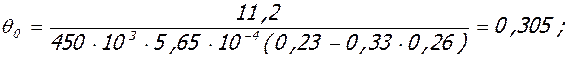
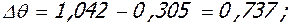
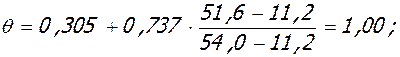
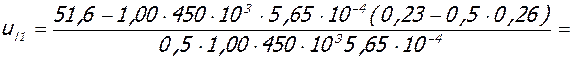 0.206м;
0.206м;
- при полной пониженной нагрузке:
M = 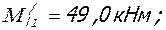
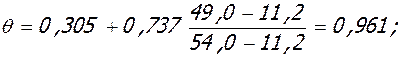
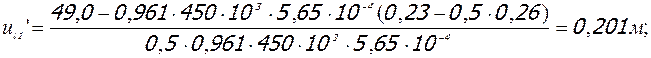
- при постоянной нагрузке:
М = 
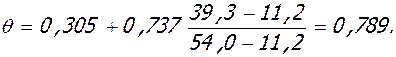
высоту трещины при постоянной нагрузке определять не требуется.
Аналогично расчет высоты u трещин, выполняют для всех расчетных сечений ригелей.
5.2. Результаты расчета коэффициента 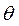 и высоты трещин u сведены в таблицу 3.
и высоты трещин u сведены в таблицу 3.
Таблица 3
| Пролеты | Расположение расчетного сечения | Несущий ригель | Нагрузка | Величина момента |М|, кНм | Значение коэффици-ента 
| Высота трещин | |
| обозна-чение | величи-на, м | ||||||
| К р а й н и й | Середина пролета | крайний | полная | 51,6 | 1,00 | Ul1 | 0,206 |
| полная пониж. | 49,0 | 0,961 | U/ l1 | 0,201 | |||
| постоянная | 39,3 | 0,789 | - | - | |||
| средний | полная | 79,2 | 1,047 | Ul2 | 0,194 | ||
| полная пониж. | 70,6 | 0,964 | U/ l2 | 0,192 | |||
| постоянная | 60,3 | 0,812 | - | - | |||
| У крайней колонны | крайний | полная | 68,2 | 1,047 | U01к | 0,191 | |
| полная пониж. | 64,5 | 0,965 | U/ l1 | 0,188 | |||
| постоянная | 52,0 | 0,815 | - | - | |||
| средний | полная | 108,3 | 1,021 | U02к | 0,157 | ||
| полная пониж. | 96,3 | 0,940 | U/02к | 0,156 | |||
| постоянная | 82,5 | 0,787 | - | - | |||
| У средней колонны | крайний | полная | 76,6 | 1,049 | U01 | 0,180 | |
| полная пониж. | 72,2 | 0,966 | U/ 01 | 0,178 | |||
| постоянная | 58,4 | 0,813 | - | - | |||
| средний | полная | 117,1 | 1,006 | U02 | 0,127 | ||
| полная пониж. | 104,5 | 0,859 | U/ 02 | 0,127 | |||
| постоянная | 89,2 | 0,717 | - | - | |||
| С р е д н и й | У колонн | крайний | полная | 76,6 | 1,049 | U012 | 0,180 |
| постоянная | 58,4 | 0,813 | - | - | |||
| средний | полная | 117,1 | 1,096 | U022 | 0,127 | ||
| постоянная | 89,2 | 0,717 | - | - | |||
| В середине пролета | крайний | полная | 48,4 | 0,990 | Ul12 | 0,205 | |
| постоянная | 36,9 | 0,780 | - | - | |||
| средний | полная | 73,8 | 1,040 | Ul22 | 0,190 | ||
| постоянная | 56,2 | 0,808 | - | - |
6. Средние относительные продольные деформации наиболее сжатой грани бетона εbc и продольной рабочей арматуры εst, (см. рис. 21 Указаний), а также среднее относительное удлинение продольной геометрической оси ε0 несущих ригелей в расчетных сечениях определяют соответственно по формулам:
εbc = ψθRb / nЕb, εst = ψθRs / nЕs, где n=0,85 - 0,40 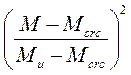 ;
;
ε0 = (εst - ωεεbc)/2; где, при распределенной нагрузке на ригель, ωε = 0,66 для сечений в середине пролета, ωε = 0,34 - для сечений у колонн.
6.1. Сечения в середине крайнего пролета крайнего ригеля:
- при полной нагрузке:
М = 51,6 кНм, θ = 1,00, ψb = 0,9, ψs = 0,75,
ν = 0,85 - 0,40(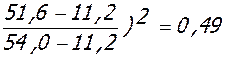 ;
;
εbc = 0,90·1,0·14,5/0,49·30·103 = 8,88·10-4;
εst = 0,75·1,0·450/0,49·200·103 = 3,44·10-3;
ε01l = (3,44·10-3 - 0,66·8,88·10-4)/2 = 1,43·10-3;
- при полной пониженной нагрузке:
М=49,0 кНм; θ = 0,961;
ν = 0,85 - 0,40 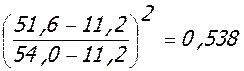 ;
;
εbc = 0,90·0,961·14,5/0,538·30·103 = 7,77·10-4;
εst = 0,75·0,961·450/0,538·200·103 = 3,01·10-3;
ε01l = (3,01·10-3 - 0,66·7,77·10-4)/2 = 1,25·10-3;
- при постоянной нагрузке:
М = 39,3 кНм; θ = 0,789;
ν = 0,85 - 0,40 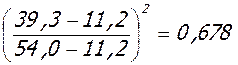 ;
;
εbc = 0,90·0,789·450/0,678·200·103 = 5,06·10-4;
εst = 0,75·0,789·450/0,678·200·103 = 1,96·10-3;
ε01l = (1,96·10-3 - 0,66·5,06·10-4)/2 = 8,13·10-4.
6.2. Результаты расчета деформаций сечений ригелей, выполненных аналогично п.6.1, сведены в табл. 4.
Таблица 4
| Про-ле т | Сечение | Нагрузка | Величина \М\, кНм | ν | Относительные деформации | |||
| от нагрузки | предельного | сжатой грани ригеля | рабочей растянутой арматуры | удлинения геометри-ческой оси | ||||
| К Р А Й Н И Й | середина пролета крайнего ригеля | полная | 51,6 | 54,0 | 0,490 | 8,88·10-4 | 3,44·10-3 | 1,43·10-3 |
| полная пониж. | 49,0 | 54,0 | 0,538 | 7,77·10-4 | 3,01·10-3 | 1,25·10-3 | ||
| постоянная | 39,3 | 54,0 | 0,678 | 5,06·10-4 | 1,96·10-3 | 8,13·10-4 | ||
| середина пролета среднего ригеля | полная | 79,2 | 79,9 | 0,458 | 9,93·10-4 | 3,85·10-3 | 1,60·10-3 | |
| полная пониж. | 70,6 | 79,9 | 0,534 | 7,86·10-4 | 3,05·10-3 | 1,26·10-3 | ||
| постоянная | 60,3 | 79,9 | 0,652 | 5,41·10-4 | 2,10·10-3 | 8,71·10-4 | ||
| у угловой колонны крайнего ригеля | полная | 68,2 | 69,0 | 0,461 | 9,88·10-4 | 3,83·10-3 | 1,75·10-3 | |
| полная пониж. | 64,5 | 69,0 | 0,535 | 7,85·10-4 | 3,04·10-3 | 1,39·10-3 | ||
| постоянная | 52,0 | 69,0 | 0,651 | 5,45·10-4 | 2,11·10-3 | 1,15·10-3 | ||
| у крайней колонны среднего ригеля | полная | 108,3 | 116,4 | 0,511 | 8,69·10-4 | 3,37·10-3 | 1,54·10-3 | |
| полная пониж. | 96,3 | 116,4 | 0,572 | 7,15·10-4 | 2,77·10-3 | 1,26·10-3 | ||
| постоянная | 82,5 | 116,4 | 0,671 | 5,10·10-4 | 2,36·10-3 | 1,10·10-3 | ||
| у средней колонны крайнего ригеля | полная | 76,6 | 78,2 | 0,469 | 9,73·10-4 | 3,78·10-3 | 1,72·10-3 | |
| полная пониж. | 72,2 | 78,2 | 0,498 | 8,44·10-4 | 3,27·10-3 | 1,49·10-3 | ||
| постоянная | 58,4 | 78,2 | 0,651 | 5,43·10-4 | 2,11·10-3 | 9,61·10-4 | ||
| у средней колонны среднего ригеля | полная | 117,1 | 142,2 | 0,591 | 7,40·10-4 | 2,87·10-3 | 1,31·10-3 | |
| полная пониж. | 104,5 | 142,2 | 0,640 | 5,84·10-4 | 2,26·10-3 | 1,03·10-3 | ||
| постоянная | 89,2 | 0,712 | 4,38·10-4 | 1,70·10-3 | 7,75·10-4 | |||
| С Р Е Д Н И Й | крайний ригель у колонны | полная | 76,6 | 78,2 | 0,469 | 9,73·10-4 | 3,78·10-3 | 1,72·10-3 |
| постоянная | 58,4 | 0,651 | 5,43·10-4 | 2,11·10-4 | 9,61·10-4 | |||
| средний ригель у колонны | полная | 117,1 | 142,2 | 0,591 | 7,40·10-4 | 2,87·10-3 | 1,31·10-3 | |
| постоянная | 89,2 | 0,712 | 4,38·10-4 | 1,70·10-3 | 7,75·10-4 | |||
| крайний ригель в середине пролета | полная | 48,4 | 54,0 | 0,548 | 7,86·10-4 | 3,05·10-3 | 1,26·10-3 | |
| постоянная | 36,9 | 0,716 | 4,74·10-4 | 1,84·10-3 | 7,63·10-4 | |||
| средний ригель в середине пролета | полная | 73,8 | 79,9 | 0,521 | 8,68·10-4 | 3,37·10-3 | 1,40·10-3 | |
| постоянная | 56,0 | 0,688 | 5,11·10-4 | 1,98·10-3 | 8,23·10-4 |
7. По величине пролетного и опорных моментов в каждом пролете ригеля определяется приложенная к ним приведенная погонная нагрузка:
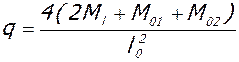 ,
,
Ml - величина момента в середине пролета, М01 и М02 - величина опорных моментов у граней колонн, l0 =6,2-0,4=5,8 м - длина рассматриваемого пролета ригеля в свету.
7.1. Для крайнего пролета крайнего ригеля.
а) полная нагрузка
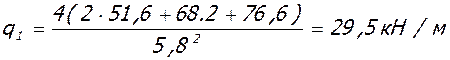
б)полная пониженная нагрузка
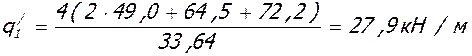
в) постоянная нагрузка
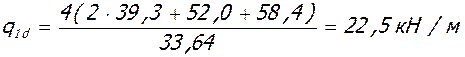
7.2. Результаты расчета приведенной погонной нагрузки на ригели сведены в таблицу 5.
Таблица 5.
| Пролет | Ригель | Нагрузка, вид | Значение погонной нагрузки q, кН/м |
| Крайний | крайний | полная | 29,5 |
| полная пониженная | 27,9 | ||
| постоянная | 22,5 | ||
| средний | полная | 45,6 | |
| полная пониженная | 41,8 | ||
| постоянная | 34,7 | ||
| Средний | крайний | полная | 29,7 |
| постоянная | 22,4 | ||
| средний | полная | 45,4 | |
| постоянная | 34,5 |
8. Длина участков пролетов ригелей с трещинами:
- в середине пролета lcrcl = l0 – 2x1;
где: l0 - длина пролета ригеля в свету между гранями колонн,
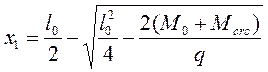 , q и М - см. п.7, выше.
, q и М - см. п.7, выше.
- у колонн 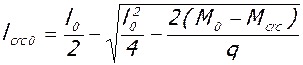
8.1. Длина участков с трещинами крайнего ригеля в крайнем пролете.
а) при полной нагрузке.
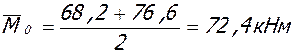 , Мcrc = 11,2 кНм,
, Мcrc = 11,2 кНм,
q1 = 29,5 кН/м,
l0 = 6,2-0,4 = 5,8 м.
- в пролете
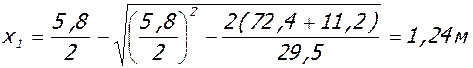 ,
,
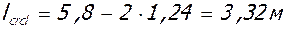 ;
;
- у колонн
 ;
;
б) при полной пониженной нагрузке:
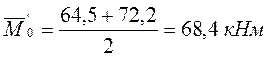 ; q' = 27,0 кН/м;
; q' = 27,0 кН/м;
- в пролете:
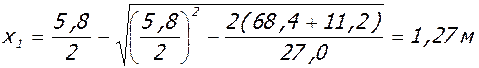 ,
,
lcrcl = 5,8-2·1,27 = 3,26 м;
- у колонн
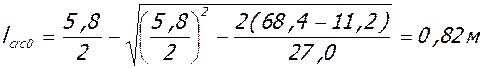 ;
;
в) при постоянной нагрузке:
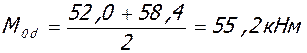 ; qd = 22,5 кН/м.
; qd = 22,5 кН/м.
- в пролете:
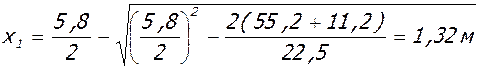 ;
;
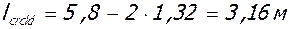 ;
;
- у колонн:
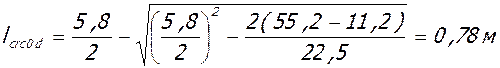 .
.
7.2. Результаты расчета длин участков ригелей с трещинами, определенные аналогично п. 7.1 сведены в таблицу 6.
Таблица 6.
| Пролет | Ригель | Нагрузка | Среднее значение опорного момента 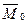 , кН/м , кН/м
| Длина участков с трещинами, м | |
| в пролете lcrcl, м | у колонн lcrc0, м | ||||
| Крайний | крайний | полная | 72,4 | 3,32 | 0,84 |
| полная пониж. | 68,4 | 3,26 | 0,82 | ||
| постоянная | 55,2 | 3,16 | 0,78 | ||
| средний | полная | 112,7 | 3,38 | 0,88 | |
| полная пониж. | 103,3 | 3,34 | 0,87 | ||
| постоянная | 85,8 | 3,26 | 0,83 | ||
| Средний | крайний | полная | 76,6 | 3,16 | 0,90 |
| постоянная | 58,4 | 2,96 | 0,85 | ||
| средний | полная | 117,1 | 3,24 | 0,93 | |
| постоянная | 89,2 | 3,12 | 0,89 |
9. Абсолютное удлинение продольной оси каждого пролета li несущих ригелей, вызванное образованием поперечных вертикальных трещин, определяется из выражения:
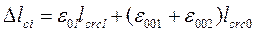 ,
,
где значения ε0l и ε00, lcrcl и lcrc0 см. табл. 4 и 6.
9.1. Абсолютное удлинение оси крайнего пролета крайнего ригеля.
а) от полной нагрузки:
ε0l = 1,43·10-3; ε001 = 1,75·10-3; ε002 = 1,72·10-3 (табл. 4)
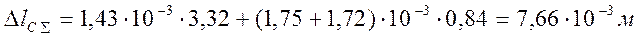 ;
;
б) от полной пониженной нагрузки:
ε0l = 1,25·10-3; ε001 = 1,39·10-3; ε002 = 1,49·10-3 (табл. 4)
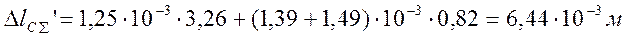 ;
;
в) от постоянной нагрузки:
ε0l = 8,13·10-4; ε001 = 1,15·10-3; ε002 = 9,61·10-4 (табл. 4)
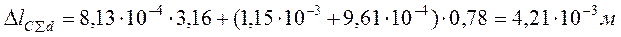 .
.
9.2. Результаты расчета абсолютного удлинения продольной оси каждого пролета ригелей, вызванного образованием поперечных трещин, сведены в таблицу 7.
Таблица 7
| Пролет | Ригель | Нагрузка | Абсолютное удлинение продольной оси ригеля, Δl, м |
| Крайний | крайний | полная | 7,66·10-3 |
| полная пониж. | 6,44·10-3 | ||
| постоянная | 4,21·10-3 | ||
| средний | полная | 7,92·10-3 | |
| полная пониж. | 6,20·10-3 | ||
| постоянная | 4,40·10-3 | ||
| Средний | крайний | полная | 7,52·10-3 |
| постоянная | 3,89·10-3 | ||
| средний | полная | 6,97·10-3 | |
| постоянная | 3,95·10-3 |
10. Величина продольного распора в несущих ригелях.
10.1. В крайних пролетах величину распора Hr рассчитывают по величине удлинения продольной оси ригеля, создаваемого приращением временной нагрузки в пределах от пониженной полной до полной, по жесткостному отпору колонн и бортовых связевых ригелей наружного контура каркаса. Расчет с учетом указанных факторов выполняется по формуле:
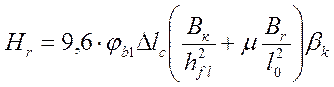 ,
,
где: φb1 = 0,85 - коэффициент, учитывающий кратковременную ползучесть бетона при изменениях временной нагрузки; ∆lc - приращение удлинения несущих ригелей в крайних пролетах от перепада нагрузки (табл. 7); Вk - жесткость поперечного сечения колонны при изгибе; Вr - то же, связевого ригеля при изгибе в горизонтальной плоскости; hfl и l0 - высота этажа и длина в свету пролета примыкающих связевых ригелей, соответственно; βk - коэффициент, учитывающий условия примыкания к бортовому ригелю, βk=0,9, m=0,65 - при примыкании рассчитываемого несущего ригеля к угловой колонне и βk=1,2, m=1,0 - при примыкании несущего ригеля к колоннам бокового ряда.
Для настоящего примера:
Вк = ЕbIк = 30·106·0,44/12 = 64000 кНм2,
Вr = 30·106·0,26·0,53/12= 81250 кНм2, hfl = 3,0 м; l0 = 5,8 м.
Для крайнего ригеля величина Hr составляет при
∆lc = 7,66·10-3 - 6,44·10-3 = 1,22·10-3 м (см. табл. 7)
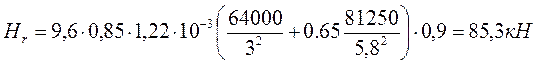
Для среднего ригеля величина Hr составляет при
∆lc = 7,92·10-3 - 6,20·10-3 = 1,72·10-3 м (см. табл. 7)
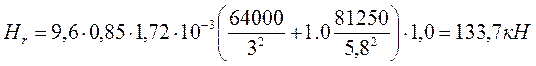
10.2. В средних пролетах ригелей величину реактивного продольного распора определяют по величине удлинения их продольной оси от полной нагрузки за вычетом удлинения, вызванного постоянной и длительной нагрузкой и рассчитывают по формуле:
 ,
,
но не более
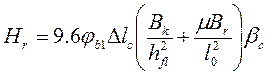 (*)
(*)
здесь: 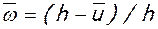 - коэффициент, учитывающий влияние высоты u трещин на жесткость сечения ригеля,
- коэффициент, учитывающий влияние высоты u трещин на жесткость сечения ригеля, 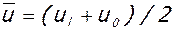 - средняя наибольшая высота трещин в пролете (ul) и у колонн (u0); b и h - ширина и высота сечения ригеля, в котором определяется продольный распор, bс=2,05 и m=0,65 – для крайнего несущего ригеля, bс=2,25 и m=1,0 – для среднего несущего ригеля, остальные обозначения приведены выше.
- средняя наибольшая высота трещин в пролете (ul) и у колонн (u0); b и h - ширина и высота сечения ригеля, в котором определяется продольный распор, bс=2,05 и m=0,65 – для крайнего несущего ригеля, bс=2,25 и m=1,0 – для среднего несущего ригеля, остальные обозначения приведены выше.
Для крайнего ригеля: b = 0,5 м, h = 0,26 м, l0 = 5,8 м
 (см. табл. 3);
(см. табл. 3); 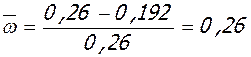 ;
;
 (см. табл. 7)
(см. табл. 7)
 (см. табл. 4)
(см. табл. 4)
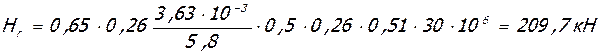
Проверка условия (*): при
Br = Eb h bw3 / 12 = 30·106·0.26·0.53 / 12 = 81250 кНм2;
Принято: Hr = 209,7 < 527,1 кН.
Для среднего ригеля: b = 0,6 м
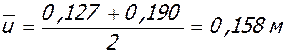 ;
; 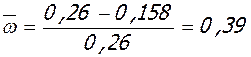 ;
;
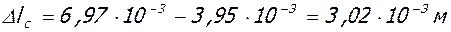 ;
; 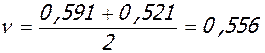 ;
;
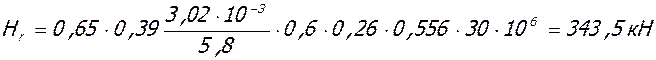
Проверка условия (*):
Принято: Hr = 343,5 < 528,2 кН.
11. Величина моментов, разгружающих расчетные сечения несущих ригелей при действии продольного распора, определяют по формуле:
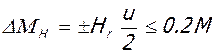 ,
,
где M – значение изгибающего момента от полной расчетной нагрузки, определенное в рассматриваемом сечении по упругому расчету каркаса; u - высота трещины в расчетном сечении ригеля от полной расчетной нагрузки (см. табл. 3).
11.1. В крайнем пролете крайнего ригеля Hr = 77,8 кН
- в середине пролета u = 0,201 м; М=51,6 кНм
\∆М\=77,8·0,201/2=7,8 кНм < 0.2∙51,6=10,3 кНм
- у крайней (угловой) колонны u = 0,191 м; М=68,2 кНм
\∆М\=77,8∙0,191/2=7,4 кНм < 0.2∙68,2=13,6 кНм
- у средней колонны u = 0,180 м; М=76,6 кНм
\∆М\=77,8∙0,180/2=7,0 кНм < 0.2∙76,6=15,3 кНм
11.2. В среднем пролете крайнего ригеля Hr = 209,7 кН
- в середине пролета u = 0,205 м; М = 48,4 кНм;
\∆М\=209,7∙0,205/2=21,5 кНм > 0.2∙48.4=9,7 кНм
- у колонн u = 0,180 м; М = 76.6 кНм;
\∆М\=209,7∙0,180/2=18,9 кНм > 0.2∙76.6=15,3 кНм
11.3. В крайнем пролете среднего ригеля Hr = 160,4 кН
- в середине пролета u = 0,194 м; М = 79,2 кНм;
\∆М\=133.7∙0,194/2=13,0 кНм < 0.2∙79.2=15,8 кНм
- у крайней колонны u = 0,157 м; М = 108,3 кНм;
\∆М\=133.7∙0,157/2=10,5 кНм < 0.2∙108.3=21,7 кНм;
- у средней колонны u = 0,127 м; М = 117,1 кНм.
\∆М\=133.7∙0,127/2=8,5 кНм < 0.2∙117.1=23,4 кНм;
11.4. В среднем пролете среднего ригеля Hr = 343,5 кН
- в середине пролета u = 0,190 м; М = 73,8 кНм;
\∆М\=343,5∙0,190/2=32,6 кНм > 0.2∙73.8=14,8 кНм;
- у колонн u = 0,127 м; М = 117,1 кНм.
\∆М\=343,5∙0,127/2=21,8 кНм < 0.2∙117.1=23,4 кНм;
12. Абсолютные значения величины моментов Мн в расчетных сечениях ригелей от действия полной расчетной нагрузки с учетом распора Нr определяем по меньшему значению ∆М, определенному выше в п. 11.
|Мн| = |М| - |∆Мн|,
где |М| - значение по модулю величины момента, определенной по упругому расчету каркаса.
Таким образом, значение величины момента М для окончательного определения требуемой площади сечения рабочей арматуры в расчетных сечениях расчетных ригелей могут быть установлены.
12.1. В крайнем пролете крайнего ригеля:
- в середине пролета Мн = 51,6-7,8=43,8 кНм;
- у средней колонны Мн = 76,6-7,4=69,2 кНм;
- у крайней (угловой) колонны Мн = 68,2-7,0=61,2 кНм.
12.2. В среднем пролете крайнего ригеля:
- в середине пролета Мн = 48,4-9,7=38,7 кНм;
- у колонн Мн = 76,6-15,3=61,3 кНм;
12.3. В крайнем пролете среднего ригеля:
- в середине пролета Мн = 79,2-13,0=66,2 кНм;
- у средней колонны Мн = 117,1-8,5=108,6 кНм.
- у угловой колонны Мн = 108,3-10,5=97,8 кНм;
12.4. В среднем пролете среднего ригеля:
- в середине пролета Мн = 73,8-14,8=59,0 кНм;
- у колонн Мн = 117,1-21,8=96,0 кНм.
12.5. С учетом установленных значений Мн произведен перерасчет требуемого сечения рабочей арматуры в ригелях. Результаты расчета представлены в табл. 8. Согласно исходным условиям примера: рабочее армирование - сталь класса А500с, бетон класса B25.
Таблица 8
| Пролет | Ригель | Сечение | Начальные значения | Окончательное значение | |||||
| |М|, кНм | Рабочее армирование | |Мн|, кНм | Рабочее армирование | Сокращение площади сечения рабочей арматуры, % | |||||
| Вид | Площадь, м2 | Вид | Площадь, м2 | ||||||
| Крайний | Крайний | середина пролета | 51,6 | 5ø12 Ат500С | 5,65·10-4 | 43,8 | 4ø12 А500с | 4,52·10-4 | 20,0 |
| у крайней колонны | 68,2 | 2ø20 + 1ø12 | 7,41·10-4 | 61,2 | 2ø20 + 1ø8 | 6,78·10-4 | 8,5 | ||
| у средней колонны | 76,6 | 2 ø20 + 2ø12 | 8,54·10-4 | 69,2 | 2ø20 + 1ø12 | 7,41·10-4 | 13,2 | ||
| Средний | середина пролета | 79,2 | 2ø20 + 2 ø12 | 8,54·10-4 | 66,2 | 2ø20 +1 ø12 | 7,41·10-4 | 13,2 | |
| у крайней колонны | 108,3 | 2 ø25 + 3 ø12 | 1,32·10-3 | 97,8 | 3ø20 +1ø12 | 1,17·10-3 | 11,4 | ||
| у средней колонны | 117,1 | 3 ø25 + 2 ø12 | 1,70·10-3 | 108,6 | 4ø20 | 1,26·10-3 | 25,9 | ||
| Средний | Крайний | середина пролета | 48,4 | 5 ø12 | 5,65·10-4 | 38,7 | 4ø12 | 4,52·10-4 | 20,0 |
| у колонны | 76,6 | 2 ø20 + 2 ø12 | 8,54·10-4 | 61,3 | 2ø20 + 1ø8 | 6,78·10-4 | 20,6 | ||
| Средний | середина пролета | 73,8 | 2 ø20 + 2 ø12 | 8,54·10-4 | 59,0 | 2ø20 | 6,28·10-4 | 26,5 | |
| у колонны | 117,1 | 3 ø25 + 2 ø12 | 1,70·10-3 | 96,0 | 4ø20 | 1,26·10-3 | 25,9 |
Вывод. С учетом влияния продольного реактивного распора Hr.окончательную площадь сечения рабочей арматуры несущих ригелей следует принять по данным табл. 8.
Date: 2015-07-27; view: 716; Нарушение авторских прав