Уравнения движения

Плоскопараллельным (плоским) называется такое движение твердого тела, при котором все точки тела перемещаются в плоскостях, параллельных некоторой заданной неподвижной плоскости (основной плоскости). Примерами тел, совершающих плоскопараллельное движение, являются: тело с плоской гранью, соприкасающееся при движении всей этой гранью с неподвижной плоскостью (рис. 97, а); шатун АВ кривошипно-ползунного механизма (рис. 97, б); отдельные звенья роботов-манипуляторов (звено АВ на рис. 97, в); зубчатые колеса в сложных зубчатых передачах (колесо с осью А на рис. 97, г) и др.

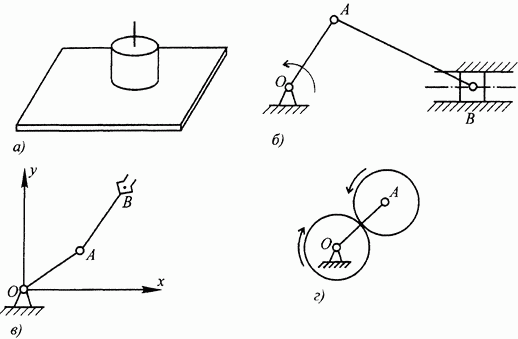
Рис. 97.

Пусть имеем тело, которое совершает плоскопараллельное движение (рис. 98). Проведем вспомогательную плоскость П, параллельную основной плоскости так, чтобы она пересекла тело. В сечении получим некоторую плоскую фигуру S. При движении тела его плоская фигура S будет перемещаться, оставаясь все время в своей плоскости П.

Выберем на плоской фигуре точки А, В, С,... и проведем через эти точки прямые 1-1, 2-2, 3-3,..., перпендикулярные плоской фигуре. Поскольку плоская фигура движется в своей плоскости, указанные прямые будут перемещаться, оставаясь все время параллельными самим себе, то есть будут двигаться поступательно. Следовательно, все точки прямой 1-1 будут двигаться одинаково, точно так же, как точка А этой прямой, принадлежащая плоской фигуре S, все точки прямой 2-2 - точно так же, как точка В плоской фигуры S и так далее.

Отсюда следует вывод: при изучении плоскопараллелъного движения тела достаточно ограничиться изучением движения какой-либо плоской фигуры этого тела, движущейся в своей плоскости.

Пусть S - какая-либо плоская фигура тела, - неподвижные координатные оси, расположенные в той же плоскости (рис. 99). Выясним, каким образом можно задавать движение плоской фигуры при помощи уравнений.

Выберем на фигуре произвольную точку О, которую будем называть полюсом, и построим координатные оси 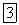, неизменно связанные с этой фигурой и движущиеся вместе с ней. Положение плоской фигуры S будет однозначно определено, если будет известно положение осей относительно осей 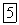. Но положение одной плоской системы координат относительно другой, расположенной в той же плоскости, будет определено, если задать три скалярные величины -координаты подвижного начала (полюса О) и угол , который ось х подвижной системы координат образует с осью неподвижной системы координат. А если эти величины известны как функции времени то положение подвижных осей, а, следовательно, и положение плоской фигуры, будет известно для каждого момента времени.

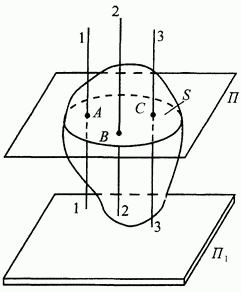
Рис. 98

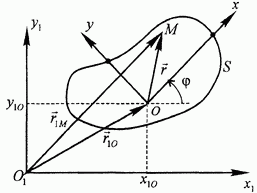
Рис. 99.

Поэтому эти равенства есть не что иное как уравнения движения плоской фигуры, движущейся в своей плоскости, или, что то же самое, уравнения плоскопараллельного движения тела.

Date: 2015-07-27; view: 367; Нарушение авторских прав