
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Потребление основных продуктов питания на одного члена семьи, кг/год
|
|
| Продукты | ||||||
| Мясо и мясопродукты | 80,0 | 78,4 | 74,1 | 68,3 | 58,7 | 63,2 |
| Молоко и молочные продукты | 411,2 | 389,6 | 378,9 | 345,4 | 280,4 | 285,6 |
| Хлебные продукты | 101,2 | 91,6 | 85,7 | 91,8 | 98,0 | 105,8 |
5.2. Правила построения рядов динамики
При составлении ряда, динамики должны выполняться следующие требования.
1. Периодизация развития, т. е. расчленение его во времени на однородные этапы, в пределах которых показатель подчиняется одному закону развития. Это, по существу, типологическая группировка во времени. Периодизация может осуществляться несколькими методами.
2. Статистические данные должны быть сопоставимы по территории, кругу охватываемых объектов, единицам измерения, времени регистрации, ценам, методологии расчета.
3. Величины временных интервалов должны соответствовать интенсивности изучаемых процессов. Чем больше вариация уровней во времени, тем чаще следует делать замеры. Соответственно для стабильных процессов интервалы можно увеличить.
Так, переписи населения достаточно проводить один раз в десять лет; учет национального дохода, урожая ведется раз в год, ежедневно регистрируются курсы покупки и продажи валют, ежечасно - температура воздуха и т. п.
4. Числовые уровни рядов динамики должны быть упорядоченными во времени. Не допускается анализ рядов с пропусками отдельных уровней, если же такие пропуски неизбежны, то их восполняют условными расчетными значениями.
5.3. Показатели анализа рядов динамики
Динамический ряд представляет собой ряд последовательных уровней, при сопоставлении которых между собой можно получить характеристику скорости и интенсивности развития явления. В результате сравнения уровней получается система абсолютных и относительных показателей динамики. К числу которых относятся: абсолютный прирост 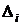 ; коэффициент роста
; коэффициент роста 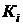 ; темп роста
; темп роста 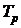 .Если сравнению подлежат несколько последовательных уровней, то возможны два варианта сопоставления:
.Если сравнению подлежат несколько последовательных уровней, то возможны два варианта сопоставления:
1. Каждый уровень динамического ряда сравнивается с одним и тем же предшествующим уровнем, принятым за базу сравнения. В качестве базисного уровня выбирается уровень, с которого начинается какой-то новый этап развития явления. Такое сравнение называется сравнением с постоянной базой.
2. Каждый уровень динамического ряда сравнивается непосредственно с предшествующим. Такое сравнение называется сравнением с переменной базой.
Показатели динамики с постоянной базой (базисные показатели) характеризуют окончательный результат всех изменений в уровнях ряда от периода к которому относится базисный уровень, до данного (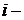 го) периода. Показатели динамики с переменной базой (цепные показатели) характеризуют интенсивность изменения уровня от периода к периоду (или от даты к дате) в пределах изучаемого промежутка времени.
го) периода. Показатели динамики с переменной базой (цепные показатели) характеризуют интенсивность изменения уровня от периода к периоду (или от даты к дате) в пределах изучаемого промежутка времени.
Абсолютный прирост 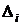 определяется как разность между двумя уровнями динамического ряда и показывает, насколько данный уровень ряда превышает уровень, принятый за базу сравнения:
определяется как разность между двумя уровнями динамического ряда и показывает, насколько данный уровень ряда превышает уровень, принятый за базу сравнения:
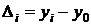 ,
,
где 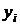 — уровень сравниваемого периода;
— уровень сравниваемого периода; 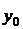 — уровень базисного периода.
— уровень базисного периода.
При сравнении с переменной базой абсолютный прирост
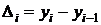 ,
,
где 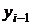 — уровень непосредственно предшествующего периода.
— уровень непосредственно предшествующего периода.
Абсолютный прирост с переменной базой называют скоростью роста или цепным абсолютным приростом.
Коэффициент роста определяется как отношение двух сравниваемых уровней и показывает во сколько раз данный уровень превышает уровень базисного периода:
при сравнении с постоянной базой 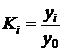 ;
;
при сравнении с переменной базой 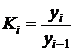 .
.
Коэффициент роста выраженный в процентах называется темпом роста: 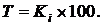
Рассмотрим расчет вышеуказанных показателей по ряду динамики ввода в действие жилых домов, построенных жилищно-строительными кооперативами в России, табл. 5.4.
Система средних показателей динамики включает:
1) средний уровень ряда;
2) средний коэффициент роста;
3) средний темп роста;
4) средний абсолютный прирост.
Средний уровень ряда — это показатель, это показатель, обобщающий итоги развития явления за единичный интервал или момент из имеющейся временной последовательности. Расчет среднего уровня ряда динамики определяется видом этого ряда и величиной интервала, соответствующего каждому уровню.
Для интервальных рядов с равными периодами времени средний уровень 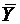 рассчитывается следующим образом:
рассчитывается следующим образом:
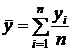 или
или 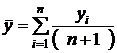 ,
,
где 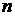 или (
или (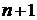 )— общая длина временного ряда или общее число равных временных отрезков, каждому из которых соответствует свой уровень
)— общая длина временного ряда или общее число равных временных отрезков, каждому из которых соответствует свой уровень 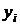 (
(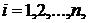 или
или 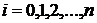 ).
).
Таблица 5.4
Ввод в действие жилых домов, построенных жилищно-строительными кооперативами в России
| Годы | Всего, млн.кв. м | Коэффициенты роста по сравнению | Темпы роста по сравнению | ||
| с 2003 г. | с предшествующим годом | с 2003 г. | с предшествующим годом | ||
| 2,9 | — | — | — | — | |
| 2,4 | 0,8276 | 0,8276 | 82,76 | 82,76 | |
| 2,1 | 0,7241 | 0,8570 | 72,41 | 85,70 | |
| 1,9 | 0,6552 | 0,9048 | 65,52 | 90,48 | |
| 1,8 | 0,6207 | 0,9474 | 62,07 | 94,74 |
Если в интервальном ряду отрезки имеют неравную длительность, то средний уровень рассчитывается по формуле средней арифметической:
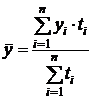 или
или 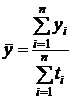 .
.
Выбор формулы определяется характером исходных данных, при этом числитель должен иметь реальное содержание.
Для моментных рядов величина среднего уровня зависит от того, как шло развитие явления в рамках интервалов, разделяющих отдельные наблюдения. Обычно считают, что в пределах периода, разделяющего моментные наблюдения, развитие происходило по линейному закону. Тогда общий средний уровень находится как среднее значение из средних по каждому интервалу. Для моментного ряда с равноотстоящими моментами получаем в итоге формулу средней хронологической.
Вид формулы определяется способом нумерации уровней. Если уровни нумеруются с нуля, то средняя хронологическая имеет вид
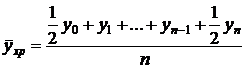 .
.
Если же уровни обозначены 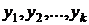 , формула принимает вид
, формула принимает вид
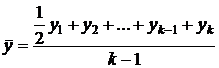 .
.
Для моментного ряда с неравными интервалами предварительно находятся значения уровней в серединах интервалов:
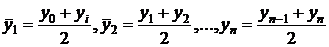 ,
,
а затем определяется общий средний уровень ряда:
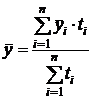 .
.
Например, определим средний месячный остаток материалов на складе предприятия в течение первого квартала текущего года. Если известно. Что остаток материалов на складе на 1 января составил 242 млн. руб.. на 1 февраля — 251 млн. руб., на 1 марта —213 млн. руб., на 1 апреля — 186 млн. руб. при вычислении среднего уровня моментного ряда условно предполагается непрерывное, равномерное изменение уровня в промежутках между двумя датами.
Основываясь на этом предположении. Определим средние остатки материалов на складе за каждый месяц как половину суммы остатков на начало и конец месяца. Средние остатки за месяц соответственно будут:
за январь — 246,5 млн. руб. 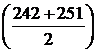 ;
;
за февраль — 232,0 млн.руб. 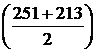 ;
;
за март — 192,5 млн. руб. 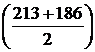 .
.
Средний остаток за квартал определяется как простая средняя арифметическая:
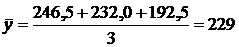 млн. руб.
млн. руб.
Приведенный расчет среднего уровня ряда можно представить формулой средней хронологической:
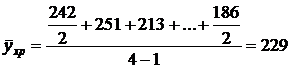 млн. руб.,
млн. руб.,
по которой в нашем примере определяют средние остатки на складе.
Средний абсолютный прирост рассчитывается по формуле:
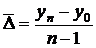 ,
,
где 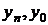 — соответственно уровень отчетного и базисного периодов ряда динамики,
— соответственно уровень отчетного и базисного периодов ряда динамики, 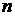 — число анализируемых периодов.
— число анализируемых периодов.
Среднегодовой темп роста: 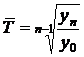 .
.
5.4. Структура ряда динамики. Проверка ряда на наличие тренда
Всякий ряд динамики теоретически может быть представлен в виде составляющих:
1) тренд — основная тенденция развития динамического ряда (к увеличению либо снижению его уровней);
2) циклические (периодические) колебания, в том числе сезонные;
3) случайные колебания.
Выявление основной тенденции развития (тренда) называется в статистике также выравниванием временного ряда, а методы выявления основной тенденции — методами выравнивания [3]. Для того чтобы представить количественную модель, выражающую общую тенденцию изменения уровней динамического ряда во времени, используют аналитическое выравнивание ряда динамики. В этом случае фактические уровни заменяются уровнями, вычисленными на основе определенной модели (уравнения). Предполагается, что она отражает общую тенденцию изменения во времени изучаемого показателя.
При аналитическом выравнивании ряда динамики, закономерно, изменяющийся уровень изучаемого показателя оценивать как функцию времени 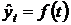 , где
, где 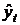 — уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени
— уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени 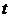 .
.
Рассмотрим аналитическое выравнивание ряда динамики по прямой, т.е. аналитическое уравнение вида
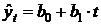 ,
,
где 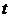 — порядковый номер периодов или моментов времени.
— порядковый номер периодов или моментов времени.
Параметры 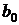 и
и 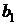 прямой рассчитываются по методу наименьших квадратов. Система нормальных уравнений в данном случае имеет вид:
прямой рассчитываются по методу наименьших квадратов. Система нормальных уравнений в данном случае имеет вид:
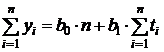 ;
;
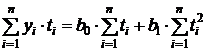 .
. 
Расчет параметров уравнения можно упростить, если отсчет времени производить так, чтобы сумма показателей времени изучаемого ряда динамики была равна нулю 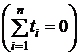 . При нечетном числе уровней ряда динамики для этого, уровень находящийся в середине ряда, принимается за условное начало отсчета времени (этому периоду или моменту времени придается нулевое значение). Даты времени, стоящие выше этого уровня, обозначаются натуральными числами со знаком минус (-1,-2,-3 и т. д.), а ниже — натуральными числами со знаком плюс (+1,+2,+3 и т.д.).
. При нечетном числе уровней ряда динамики для этого, уровень находящийся в середине ряда, принимается за условное начало отсчета времени (этому периоду или моменту времени придается нулевое значение). Даты времени, стоящие выше этого уровня, обозначаются натуральными числами со знаком минус (-1,-2,-3 и т. д.), а ниже — натуральными числами со знаком плюс (+1,+2,+3 и т.д.).
Если число уровней динамического ряда четное, периоды времени в порядке возрастания с единицы и т.д.
Когда 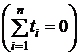 система нормальных уравнений преобразуется следующим образом:
система нормальных уравнений преобразуется следующим образом:
 ;
;
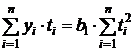 .
.
Откуда 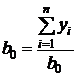 ;
; 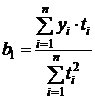 .
.
Рассмотрим аналитическое выравнивание по прямой ряда динамики строительства жилья жилищно-строительными кооперативами в России (см. табл. 5.4). Расчет параметров представлен в табл. 5.5.
Используя итоги граф 2, 4 и 5, определяем параметры уравнения прямой:
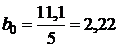 ;
; 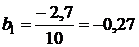 .
.
По рассчитанным параметрам записывается уравнение прямой динамики, характеризующее строительство жилья жилищно-строительными кооперативами:
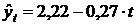 .
.
Табл. 5.5
Данные для расчета показателей выравненной динамики
| Годы | Всего
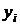 ,
млн. м ,
млн. м 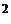
| Условное
обозначение
периодов
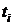
| 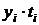
| 
| Уровень
выравненной динамики,
млн. м 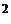
|
| 2,9 | -2 
| -5,8 | 2,76 | ||
| 2,4 | -1 | -2,4 | 2,49 | ||
| 2,1 | 2.22 | ||||
| 1,9 | +1 | 1,9 | 1,95 | ||
| 1,8 | +2 | 3,6 | 1,68 | ||
| ИТОГО | 11,1 | — | -2,7 | 11.1 |
Используя приведенное уравнение, рассчитаем для каждого года теоретические значения:
для 2003 года 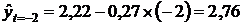 млн. м
млн. м 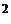 ;
;
для 2004 года 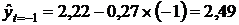 млн. м
млн. м 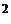 и т.д. (см. табл. 5.5, графу 6).
и т.д. (см. табл. 5.5, графу 6).
Правильность расчета уровней выравненного ряда динамики может быть проверена следующим образом: сумма значений эмпирического ряда, т.е. 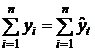 (табл. 5.5, графы 2 и 6).
(табл. 5.5, графы 2 и 6).
5.5. Анализ сезонных колебаний
Если в анализируемой временной последовательности наблюдаются устойчивые отклонения от тенденции (как в большую, так и в меньшую сторону), то можно предположить наличие в ряду динамики некоторых (одного или нескольких) колебательных процессов. Это особенно заметно, когда изучаемые явления имеют сезонный характер, – возрастание или убывание уровней повторяется регулярно с интервалом в один год (например, производство молока и мяса по месяцам года, потребление топлива и электроэнергии для бытовых нужд, сезонная продажа товаров и т. д.) [3].
Для измерения сезонных колебаний статистикой предложены различные методы. Наиболее простые и часто употребляемые из них:
1) метод абсолютных разностей;
2) метод относительных разностей;
3) построение индексов сезонности.
Первые два способа предполагают нахождение разностей фактических уровней и уровней. найденных при выявлении основной тенденции развития.
Остановимся на третьем способе. Для измерения сезонных колебаний необходимы данные не менее чем за трехлетний период. Важной характеристикой сезонных колебаний является индекс сезонности. В простейшем варианте этот показатель рассчитывается как отношение среднего уровня соответствующего месяца к общей средней за все месяцы нескольких лет [4].
Индексы сезонности могут быть рассчитаны так же как отношение фактического уровня соответствующего месяца к уровню, рассчитанному по методу скользящей средней или же определенному по уравнению тренда. В последнем случае предварительно для временного ряда рассчитывается уравнение тренда, на основании которого за каждый месяц определяется значение выравненного уровня.
Тогда индекс сезонности рассчитывается следующим образом:
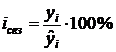 ,
,
где 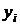 — фактическое значение уровня динамического ряда;
— фактическое значение уровня динамического ряда; 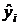 — значение выравненного уровня
— значение выравненного уровня 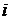 -го месяца.
-го месяца.
Индексы сезонности показывают, во сколько раз фактический уровень ряда в момент или интервал времени 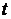 больше среднего уровня либо уровня, вычисляемого по уравнению тенденции
больше среднего уровня либо уровня, вычисляемого по уравнению тенденции 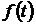 . При анализе сезонности уровни временного ряда показывают развитие явления по месяцам (кварталам) одного или нескольких лет. Для каждого месяца (квартала) получают обобщенный индекс сезонности как среднюю арифметическую из одноименных индексов каждого года. Индексы сезонности – это, по существу, относительные величины координации, когда за базу сравнения принят либо средний уровень ряда, либо уровень тенденции. Способы определения индексов сезонности зависят от наличия или отсутствия основной тенденции.
. При анализе сезонности уровни временного ряда показывают развитие явления по месяцам (кварталам) одного или нескольких лет. Для каждого месяца (квартала) получают обобщенный индекс сезонности как среднюю арифметическую из одноименных индексов каждого года. Индексы сезонности – это, по существу, относительные величины координации, когда за базу сравнения принят либо средний уровень ряда, либо уровень тенденции. Способы определения индексов сезонности зависят от наличия или отсутствия основной тенденции.
Если тренда нет или он незначителен, то для каждого месяца (квартала)
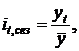
где 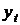 — уровень показателя за месяц (квартал)
— уровень показателя за месяц (квартал) 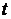 ;
; 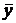 — общий средний уровень показателя.
— общий средний уровень показателя.
Как отмечалось выше, для обеспечения устойчивости показателей можно взять больший промежуток времени. В этом случае
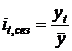 , либо
, либо 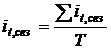 ,
,
где 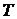 — число лет.
— число лет.
В качестве примера используем данные об объеме продаж акций на 15 крупнейших биржах России (млн. руб.) из табл. 5.6:
Таблица 5.6
Данные об объеме продаж на крупнейших биржах России, млн. руб.
| Месяц | Уровень показателя (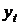 ) )
| 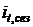
|
| Январь | 12,78 | 0,027 |
| Февраль | 122,08 | 0,254 |
| Март | 709,98 | 1,477 |
| Апрель | 1602,61 | 3,334 |
| Май | 651,83 | 1,356 |
| Июнь | 220,80 | 0,459 |
| Июль | 327,68 | 0,682 |
| Август | 277,12 | 0,576 |
| Сентябрь | 418,31 | 0,870 |
| Октябрь | 521,18 | 1,084 |
| Ноябрь | 396,20 | 0,824 |
| Декабрь | 508,34 | 1,057 |
Общий средний уровень показателя:
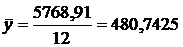 млн. руб. в месяц.
млн. руб. в месяц.
Как видно в течение года были зарегистрированы три пика объемов продаж акций: в апреле, октябре и декабре.
При наличии тренда индекс сезонности определяется на основе методов, исключающих влияние тенденции. Порядок расчета следующий:
1) для каждого уровня определяют выравненные значения по тренду 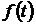 ;
;
2) рассчитывают отношения 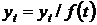 ;
;
3) при необходимости находят среднее из этих отношений для одноименных месяцев (кварталов):
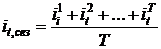 .
.
6. ИНДЕКСЫ И ИХ ИСПОЛЬЗОВАНИЕ В ЭКОНОМИКО-СТАТИСТИЧЕСКИХ ИССЛЕДОВАНИЯХ
Индекс представляет собой относительную величину, полученную в результате сопоставления уровней сложных социально-экономических показателей во времени, в пространстве или с планом [3].
С помощью индексных показателей решаются следующие основные задачи:
1) характеристика общего изменения сложного экономического показателя (например, затрат на производство продукции, стоимости произведенной продукции и т.д. или формирующих его отдельные показателей-факторов;
2) выделение в изменении сложного показателя одного из факторов путем выявления других факторов (например, увеличение выручки от реализации продукции, связанное с ростом цен или выпуска продукции в натуральном выражении).
По степени охвата элементов совокупности различают индивидуальные и сводные (общие) индексы.
Индивидуальными называются индексы, характеризующие изменение только одного элемента совокупности (например, изменение только одного элемента совокупности 9например, изменение выпуска легковых автомобилей определенной марки). Индивидуальный индекс цен по отдельным видам продукции
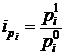 .
.
Сводный индекс цен отражает изменение по всей совокупности элементов сложного явления. Сводный индекс характеризует динамику объема промышленной продукции. Обозначают сводный (общий) индеек буквой 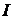 .
.
При вычислении индексов различают сравниваемый уровень и уровень, с которым производится сравнение, называемый базисным. При этом возможны два способа расчета индексов — цепной и базисный. Цепные индексы получают путем сопоставления текущих уровней с предшествующим. Таким образом, база сравнения непрерывно меняется. Базисные индексы получают путем сопоставления с уровнем периода, принятого за базу сравнения.
При использовании индексов как показателей выполнения плана за базу сравнения принимают плановые показатели.
В зависимости от методологии расчета различают агрегатные индексы и средние из индивидуальных индексов. Последние, в свою очередь, делятся на средние арифметические и средние гармонические индексы.
Если разделить стоимость продукции отчетного периода на стоимость продукции базисного периода, получим индекс стоимости. В общем виде его можно записать так:
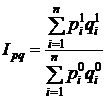 ,
,
где 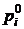 ,
, 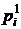 — цена единицы отдельных видов продукции соответственно в базисном и отчетном периодах;
— цена единицы отдельных видов продукции соответственно в базисном и отчетном периодах; 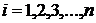 — количество отдельных видов продукции;
— количество отдельных видов продукции; 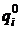 ,
, 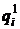 —количество единиц отдельных видов продукции соответственно в базисном и отчетном периодах.
—количество единиц отдельных видов продукции соответственно в базисном и отчетном периодах.
Если стоимость продукции в отчетном периоде выросла, то индекс стоимости будет больше 1, а если она снизилась, то будет меньше 1.
Индекс стоимости показывает изменение стоимости продукции, которая зависит от изменения уровня цен и количества выпускаемой продукции в отчетном периоде по сравнению с базисным.
Количественное представление об изменении объема выпуска продукции характеризуется индексом физического объема:
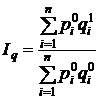 .
.
Рассмотрим порядок вычисления индексов физического объема продукции на следующем условном примере (табл. 6.1).
Таблица 6.1
Объем выпуска продукции предприятия по видам
| Вид продукции | Выпуск продукции в натуральном выражении, шт. | Цена производителя за единицу, млн. руб. | Индивидуальный индекс физического объема продукции
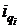
| Индивидуальный индекс цен
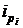
| ||
| базисный период | отчетный период | базисный период | отчетный период | |||
| Обору-дование | 2 100 | 2 000 | 75,00 | 82,50 | 0,9524 | 1,1 1,1000 |
| Литье (в тоннах) | 11 500 | 12 000 | 8,75 | 10,10 | 1,0435 | 1,1543 1,1543 |
Имеются данные о фактическом выпуске продукции машиностроительным предприятием за два года. По данным, о выпуск продукции в натуральном выражении можно рассчитать индексы, характеризующие динамику выпуска отдельных видов продукции, или индивидуальные индексы. Для вычисления индивидуальных индексов динамики определяют отношение объема выпуска продукции (табл. 6.1):
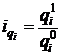 .
.
Индекс динамики объема производства оборудования составляет 95,42%, что означает снижение его выпуска на 4,76% (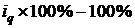 ). В динамике же выпуска литья наблюдается противоположная тенденция: выпуск литья возрос на 4,35% (1,0435
). В динамике же выпуска литья наблюдается противоположная тенденция: выпуск литья возрос на 4,35% (1,0435 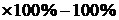 ). Общее изменение выпуска продукции предприятия может быть получено на основе определения агрегатных индексов физического объема продукции. В качестве соизмерителей используем цены базисного периода:
). Общее изменение выпуска продукции предприятия может быть получено на основе определения агрегатных индексов физического объема продукции. В качестве соизмерителей используем цены базисного периода:
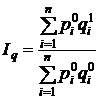 .
.
Стоимостные показатели выпуска продукции необходимые для расчета индексов, приведены в табл. 6.2.
Таблица 6.2
Расчет стоимости выпуска продукции
| Вид продукции | Стоимость выпуска тыс. руб. | Условная стоимость выпуска тыс. руб. | ||
базисный период
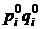
| отчетный период
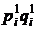
| базисный период в текущих ценах
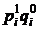
| отчетный период в текущих ценах

| |
| Оборудование | 157 500 | 165 000 | 173 250 | 150 000 |
| Литье | 100 625 | 121 200 | 116 150 | 105 000 |
| ИТОГО | 258 125 | 286 200 | 289 400 | 255 000 |
Агрегатный индекс динамики физического объема продукции:
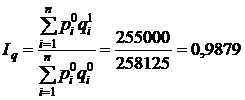 , или 98,79%.
, или 98,79%.
ОГЛАВЛЕНИЕ
| Введение……………………………………………………………………………. 1. Определение и основные понятия статистики……………………………… 2. Статистические величины 2.1. Понятие абсолютной и относительной величины в статистике…………... 2.2. Виды и взаимосвязи относительных величин……..……………………….. 2.3. Средние величины…….…………………………………………………..…. 2.4. Расчет средних по результатам группировок…….…………………….….. 2.5. Структурные средние……..…………………………………………………. 2.6. Показатели вариации………………………………………………………… 3. Статистическое наблюдение 3.1. Основные этапы статистического исследования…….…………………..… 3.2. Статистическое наблюдение – первый этап статистического исследования………………………………………………………………………. 3.3. Программно-методологические и организационные вопросы статистического наблюдения…………………………………………………...… 3.4. Формы, виды и способы наблюдения……..……………………………..….. 3.5. Понятие выборочного наблюдения отбор единиц выборочной совокупности……………………………………………………………………….. 3.6. Определение ошибок выборки……..……………………………………..…. 3.7. Определение численности выборки…….………………………………..…. 3.8. Распределение выборочных результатов…….…………………………...… 4. Сводка и группировка данных статистического наблюдения……………….. 4.1. Сводка статистических данных……..……………………………………….. 4.2. Группировка статистических данных……..……………………………..….. 5. Изучение динамики общественных явлений……………………………..…… 5.1. Ряды динамики. Классификация……..…………………………………..….. 5.2. Правила построения рядов динамики……..……………………………..….. 5.3. Показатели анализа рядов динамики ……...……………………………...… 5.4. Структура ряда динамики. Проверка ряда на наличие тренда……..……… 5.5. Анализ сезонных колебаний……..……………………………………..……. 6. Индексы и их использование в экономико-статистических исследованиях…………………………………..…….……………………..…….. Библиографический список ………..…………………………………………….. |
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики:
Учебник. – М.: ИНФРА-М, 2005. – 416 с.
2. Статистика: Учеб. пособие / Под ред. Проф. М.Р. Ефимовой. – М.: ИНФРА – М, 2005. – 336 с. – (Серия "Вопрос-ответ").
3. Статистика: Курс лекций / Харченко Л.П., Долженкова В.Г., Ионин В.Г. и др.; Под ред. к.э.н. В.Г. Ионина. – Новосибирск: Изд-во НГАЭиУ, М.: ИНФРА – М, 2005. – 310 с.
4. Статистика: Учеб. пособие / Под ред. Проф. В.М. Гусарова. – М.: ЮНИТИ, 2005. – 416 с.
Date: 2015-07-27; view: 537; Нарушение авторских прав