
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

ББК С6.я7 3 page
|
|
б) достоверности и точности данных;
в) их единообразия и сопоставимости.
3.3. Программно-методологические и организационные вопросы статистического наблюдения
Любое СИ необходимо начинать с точной формулировки его цели и конкретныхзадач. После этого определяются объект и единица наблюдения, разрабатывается программа, выбираются вид и способ наблюдения.
Объект наблюдения – совокупность социально-экономических явлений и процессов, которые подлежат исследованию, или точные границы, в пределах которых будут регистрироваться статистические сведения. Определяя объект наблюдения необходимо точно указать единицу наблюдения.
Единица наблюдения– составная часть объекта наблюдения, которая служит основой счета и обладает признаками, подлежащими регистрации при наблюдении.
Пример: при переписи населения единица наблюдения – каждый отдельный человек.
Программа наблюдения – это перечень вопросов, по которым собираются сведения, либо перечень признаков и показателей, подлежащих регистрации. Программа наблюдения оформляется в виде бланка(анкеты, формуляра), в который заносятся первичные сведения.
3.4. Формы, виды и способы наблюдения
В статистической практике используются две организационные формы наблюдения – отчетность и специальное статистическое обследование.
Отчетность - это такая организационная форма, при которой единицы наблюдения представляют сведения о своей деятельности в виде формуляров регламентированного образца. Особенность отчетности состоит в том, что она обязательно документально обоснована и юридически подтверждена подписью руководителя.
Специальное статистическое обследование – это проведение переписей населения. В 2010 году предстоит очередная перепись населения.
С точки зрения полноты охвата фактов СН может быть сплошным и не сплошным. Сплошное наблюдение представляет собой полный учет всех единиц совокупности. Не сплошное – организуют как учет части единиц совокупности, на основе которой можно получить обобщенную характеристику вей совокупности.
Способ основного массива как один из видов не сплошного наблюдения характеризуется тем, что отбирают наиболее крупные единицы наблюдения, в которых сосредоточена значительная доля всех подлежащих изучению фактов (например: обследование конъюнктуры торговых оборотов и цен на городских рынках).
Выборочным наблюдением – является такое, при котором характеристика всей совокупности дается по некоторой её части, отобранной в случайном порядке. Случайность отбора единиц гарантируется независимостью результатов выборки от воли лиц, её производящих. Таким образом, результат выборки освобождается от тенденциозных ошибок. Возникающие же случайные ошибки выборки можно определить с помощью теорем закона больших чисел и надлежащей организацией наблюдения свести их к допустимому минимуму.
Выборочный метод применяется в тех случаях. Когда проведение сплошного наблюдения невозможно или экономически нецелесообразно. Выборочное наблюдение используют также для проверки результатов сплошного наблюдения.
Ту часть единиц, которая отобрана для наблюдения, принято называть выборочной совокупностью (выборкой), а всю совокупность единиц, из которых производится отбор, – генеральной.
Качество результатов выборочного наблюдения зависит от того, насколько состав выборки репрезентативен (представителен).
Для обеспечения репрезентативности выборки необходимо соблюдение принципа случайности отбора единиц. Принцип случайности предполагает, что на включение или исключение объекта из выборки не может повлиять какой-либо фактор, кроме случая.
Особенности обследуемых объектов определяют два метода отбора единиц в выборочную совокупность – повторный (отбор по схеме возвращенного шара) и бесповторный (отбор по схеме невозвращенного шара). При повторном отборе каждая попавшая в выборку единица или серия возвращается в генеральную совокупность и имеет шанс вторично попасть в выборку. При этом вероятность попадания в выборочную совокупность всех единиц генеральной совокупности остается одинаковой. Бесповторный отбор означает, что каждая отобранная единица (или серия) не возвращается в генеральную совокупность и не может подвергнуться повторной регистрации, а поэтому для остальных единиц вероятность попасть в выборку увеличивается.
Бесповторный отбор дает более точные результаты по сравнению с повторным, так как при одном и том же объеме выборки наблюдение охватывает больше единиц генеральной совокупности. Поэтому он находит более широкое применение в статистической практике, и только в тех случаях, когда бесповторный отбор провести нельзя, используется повторная выборка (при обследовании потребительского спроса, пассажирооборота и т.п.).
3.5. Определение ошибок выборки
По мере отбора единиц в выборочную совокупность или по его завершении производится регистрация предусмотренных программой признаков. Итогом же является расчет обобщающих выборочных характеристик. Часто кроме выборочной средней (X) исчисляют также выборочную долю (W) единиц, обладающих каким-либо интересующим нас признаком, в общей их численности.
Разность между показателями выборочной и генеральной совокупности называется ошибкой выборки. Ошибки выборки подразделяются на ошибки регистрации и ошибки репрезентативности.
Ошибки регистрации возникают из-за неправильных или неточных сведений. Источниками таких ошибок могут быть непонимание существа вопроса, невнимательность регистратора, пропуск или повторный счет некоторых единиц совокупности, описки при заполнении формуляров и т. д.
Среди ошибок регистрации выделяются систематические, обусловленные причинами, действующими в каком-то одном направлении и искажающими результаты работы (например, округление цифр, тяготение к полным пятеркам, десяткам, сотням и т. д.), и случайные, проявляющиеся в различных направлениях, уравновешивающие друг друга и лишь изредка дающие заметный суммарный итог.
Ошибки репрезентативности также могут быть систематическими и случайными. Систематические ошибки репрезентативности возникают из-за неправильного, тенденциозного отбора единиц, при котором нарушается основной принцип научно организованной выборки - принцип случайности. Случайные ошибки репрезентативности означают, что, несмотря на принцип случайности отбора единиц, все же имеются расхождения между характеристиками выборочной и генеральной совокупности. Изучение и измерение случайных ошибок репрезентативности и является основной задачей выборочного метода.
Рассмотрим на примере, насколько отличаются выборочные и генеральные показатели по данным об успеваемости студентов (две 10 %-е выборки):
| Оценка | Число студентов, чел. | ||
| Генеральная совокупность совокупностьсовокупность | Первая выборка | Вторая выборка | |
| Итого |
Средний балл рассчитаем по средней арифметической взвешенной.
По генеральной совокупности
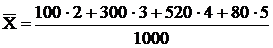 =3,58
=3,58
по первой выборке 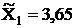 ;
;
по второй выборке 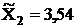 .
.
Доля студентов, получивших оценки «4» и «5»:
по генеральной совокупности 
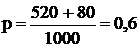 или 60%;
или 60%;
по первой выборке 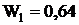 или 64%;
или 64%;
по второй выборке 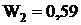 или 59%.
или 59%.
Разность между показателями выборочной и генеральной совокупности и будет случайной ошибкой репрезентативности. Ошибки репрезентативности:
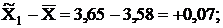
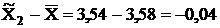 ;
;
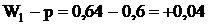 ;
;
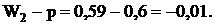
Как видно из расчетов, выборочная средняя и выборочная доля являются случайными величинами, которые могут принимать различные значения в зависимости от того, какие единицы совокупности попали в выборку. Следовательно, ошибки выборки также являются случайными величинами и могут принимать различные значения. Поэтому определяют среднюю из возможных
ошибок (обозначим ее через m). Средняя ошибка выборки равна среднему квадратическому отклонению, деленному на квадратный корень из численности выборки:
для средней 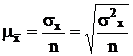 ;
;
для доли 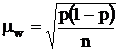 .
.
В этих формулах 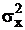 и
и 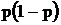 являются характеристиками генеральной совокупности, которые при выборочном наблюдении неизвестны. На практике их заменяют аналогичными характеристиками выборочной совокупности на основании закона больших чисел, по которому выборочная совокупность при достаточно большом объеме достаточно точно воспроизводит характеристики генеральной совокупности. Следовательно, средние ошибки выборки можно представить следующим образом:
являются характеристиками генеральной совокупности, которые при выборочном наблюдении неизвестны. На практике их заменяют аналогичными характеристиками выборочной совокупности на основании закона больших чисел, по которому выборочная совокупность при достаточно большом объеме достаточно точно воспроизводит характеристики генеральной совокупности. Следовательно, средние ошибки выборки можно представить следующим образом:
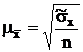 и
и 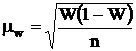 .
.
При бесповторном отборе подкоренное выражение умножается на величину 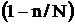 , которая всегда меньше единицы, поэтому величина средней ошибки выборки при, бесповторном отборе оказывается меньше, чем при повторном. В тех случаях, когда доля выборки незначительна и множитель
, которая всегда меньше единицы, поэтому величина средней ошибки выборки при, бесповторном отборе оказывается меньше, чем при повторном. В тех случаях, когда доля выборки незначительна и множитель 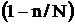 близок к единице, поправкой можно пренебречь. Для решения практических задач кроме средней пользуются предельной ошибкой выборки, которая связана с гарантирующим ее уровнем вероятности. Уровень вероятности определяет величина нормированного отклонения t, и наоборот. Значения t даются в таблицах нормального распределения вероятностей.
близок к единице, поправкой можно пренебречь. Для решения практических задач кроме средней пользуются предельной ошибкой выборки, которая связана с гарантирующим ее уровнем вероятности. Уровень вероятности определяет величина нормированного отклонения t, и наоборот. Значения t даются в таблицах нормального распределения вероятностей.
Чаще всего используют следующие сочетания;
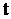
| P |
| 1,0 | 0,683 |
| 1,5 | 0,866 |
| 2,0 | 0,954 |
| 2,5 | 0,988 |
| 3,0 | 0,997 |
| 3,5 | 0,999 |
Так, если t =1, то с вероятностью 0,683 можно утверждать, что разность между выборочными и генеральными показателями не превысит одной средней ошибки. Предельные ошибки выборки (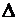 ) определяются по формулам табл. 3.1.
) определяются по формулам табл. 3.1.
После исчисления предельных ошибок выборки находят доверительные интервалы для генеральных показателей. Для 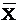 это (X ± DC). Для Р это (W ± Dw).
это (X ± DC). Для Р это (W ± Dw).
Таблица 3.1
Предельные ошибки выборки
| Метод отбора | Предельные ошибки индивидуального отбора | |
| для средней | для доли | |
| Повторный |
D= 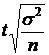
|
D= 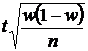 
|
| Бесповторный |
D= 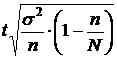  
|
D= 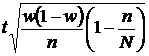
|
Из формул табл. 3.1 видно, что величина D зависит от:
1) колеблемости признака (прямая связь);
2) численности выборки (обратная связь);
3) доверительной вероятности (прямая связь);
4) метода отбора.
Формулы, приведенные в табл. 3.1, используются при определении ошибок выборки, осуществляемой собственно случайным или механическим методами.
При стратифицированном отборе в выборку обязательно попадают представители всех групп и обычно в тех же пропорциях, что и в генеральной совокупности. Поэтому ошибка выборки в Данном случае зависит главным образом от средней из групповых дисперсий (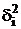 ). По правилу сложения дисперсий
). По правилу сложения дисперсий
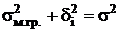
Отсюда следует, что ошибка выборки для стратифицированного отбора всегда будет меньше, чем для собственно случайного.
При серийном (гнездовом) отборе мерой колеблемости будет межгрупповая дисперсия (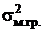 ).
).
3.6. Определение численности выборки
Разрабатывая программу выборочного наблюдения, сразу задают величину допустимой ошибки выборки и доверительную вероятность. Неизвестным остается тот минимальный объем выборки, который должен обеспечить требуемую точность. Формулы для определения численности выборки (n) зависят от метода отбора. Они различны для расчета средней и доли и следуют из формул предельных ошибок выборки (табл. 3.2).
Значения D и t определяются как задачами, стоящими перед исследователем, так и природой изучаемого явления. Чем более достоверные результаты требуется получить, тем большую вероятность необходимо задать. С увеличением допустимой ошибки уменьшается необходимый объем выборки, и наоборот (т.е., например, увеличение ошибки выборки в 2 раза уменьшит n в 4 раза). Вариация (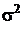 ) признака существует объективно, независимо от исследователя, но к началу выборочного наблюдения она неизвестна. Приближенно
) признака существует объективно, независимо от исследователя, но к началу выборочного наблюдения она неизвестна. Приближенно 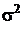 определяется следующими способами:
определяется следующими способами:
1) берут из предыдущих исследований;
2) по правилу «трех сигм» общий размах вариации укладывается в 6 сигм (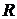 = 6
= 6 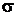 , отсюда
, отсюда 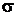 =
= 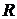 /6). Для большей точности
/6). Для большей точности 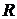 делят на 5;
делят на 5;
3) если хотя бы приблизительно известна средняя величина
изучаемого признака, то 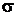 =
= 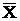 /3;
/3;
4) при изучении альтернативного признака, если нет даже приблизительных сведений о доле единиц, обладающих заданным значением этого признака, берется максимально возможная величина дисперсии, равная 0,25.
Таблица 3.2
Численность выборки при собственно случайном и механическом отборе
| Метод отбора | Формулы объема выборки | |
| для средней | для доли | |
| Повторный |
n = 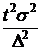
|
n= 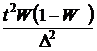 
|
| Бесповторный |
n = 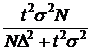
|
n=  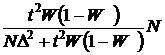
|
При стратифицированном отборе, не пропорциональном объему групп, общее число отбираемых единиц делится на количество групп. Полученная величина даст объем выборки из каждой группы.
При отборе, пропорциональном числу единиц в группе, число наблюдений по каждой группе определяется формулой
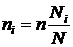 ,
,
где 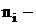 объем выборки из i-той группы;
объем выборки из i-той группы;
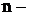 общий объем выборки;
общий объем выборки;
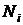
 — объем i-той группы;
— объем i-той группы;
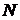 — объем генеральной совокупности.
— объем генеральной совокупности.
При отборе с учетом вариации признака, дающем минимальную величину ошибки выборки, процент выборки из каждой стратифицированной группы должен быть пропорционален среднему квадратическому отклонению в этой группе
(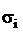 ). Расчет численности выборки (
). Расчет численности выборки (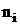 ) производится по формулам:
) производится по формулам:
для средней
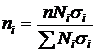 ;
;
для доли
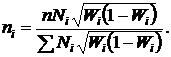
При серийном (гнездовом) отборе необходимую численность отбираемых серий определяют так же, как и при собственно случайном, только вместо N, n и 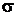 2 подставляют R, r и
2 подставляют R, r и 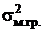 , где
, где 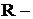 число серий в генеральной совокупности;
число серий в генеральной совокупности;
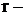 число отобранных серий;
число отобранных серий; 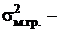 межсерийная (межгрупповая) дисперсия.
межсерийная (межгрупповая) дисперсия.
3.7. Распространение выборочных результатов
Распространение выборочных оценок на генеральную совокупность состоит в определении характеристик генеральной совокупности на основе характеристик выборочной. Применяются два способа распространения выборочных данных:
1) способ прямого пересчета;
2) способ поправочных коэффициентов.
При первом способе средние величины и доли, полученные в результате исследования выборочной совокупности, переносятся на генеральную. Если известна численность единиц этой совокупности, то можно найти общий объем признака. Например, если средняя выборочная урожайность зерновых равна 20 ц/га, а предельная ошибка выборки ± 1,5 ц/га, при известной посевной площади в 20 000 га можно установить ожидаемые пределы валового сбора (ВС) зерновых: от 18,5 - 20 000 = 37 тыс. т до 21,5 - 20 000 = 43 тыс. т с вероятностью, принятой при расчете предельной ошибки.
Второй способ используется для уточнения данных сплошного наблюдения. Так, если выборочное наблюдение показало, что недоучет величины исследуемого явления составил 0,5 %, то эту последнюю величину (поправочный коэффициент) распространяют на результат, полученный при сплошном наблюдении, путем увеличения его на 0,5 %.
4. СВОДКА И ГРУППИРОВКА ДАННЫХ СТАТИСТИЧЕСКОГО
НАБЛЮДЕНИЯ
4.1. Сводка статистических данных
Собранный в процессе статистического наблюдения материал нуждается в определенной обработке, сведении разрозненных данных воедино. Научно организованная обработка материалов наблюдения (по заранее разработанной программе), включающая в себя кроме обязательного контроля собранных данных систематизацию, группировку материалов, составление таблиц, получение итогов и производных показателей (средних, относительных величин), называется в статистике сводкой.
Сводка представляет собой второй этап статистического исследования. Целью сводки является получение на основе сведенных материалов обобщающих статистических показателей, отражающих сущность социально-экономических явлений и определенные статистические закономерности.
Статистическая сводка осуществляется по программе, которая должна разрабатываться еще до сбора статистических данных, практически одновременно с составлением плана и программы статистического наблюдения. Программа сводки включает определение
групп и подгрупп;
системы показателей;
видов таблиц.
Все эти вопросы, разумеется, следует решать не механически, а с учетом цели исследования и особенностей изучаемой совокупности. Выделение тех или иных групп должно быть обоснованным, не формальным. Кроме итоговых и групповых показателей сводка дает основу для последующего анализа и выявления различного рода закономерностей.
По технике или способу выполнения сводка может быть ручной либо механизированной. Ручная сводка применяется в основном для небольших массивов данных. Начинается она с шифровки статистических формуляров (карточек). Затем формуляры определенным образом группируются и подсчитываются их число и другие показатели. При механизированной сводке и больших объемах совокупности исходные данные могут сразу заноситься на машиночитаемые носители информации и полностью обрабатываться на ЭВМ.
4.2. Группировка статистических данных
Изучаемые статистикой массовые явления и процессы протекают в качественно однородных совокупностях. Однако качественная однородность единиц, составляющих совокупность, не является чем-то абсолютным, навсегда и на все случаи заданным. Единицы, качественно однородные в одном отношении, оказываются разнородными в другом. Это позволяет делить статистическую совокупность на частные подсовокупности - использовать методы группировки.
Таким образом, группировка - это разбиение совокупности на группы, однородные по какому-либо признаку. С точки зрения отдельных единиц совокупности группировка - это объединение отдельных единиц совокупности в группы, однородные по каким-либо признакам.
Устойчивое разграничение объектов выражается классификацией. Классификация - это как бы стандарт, в котором каждая атрибутивная запись может быть отнесена лишь к одной группе или подгруппе. Классификация основывается на самых существенных признаках, которые меняются очень мало (например, классификация отраслей народного хозяйства, классификация основных фондов и т. д.). Таким образом, классификация - это узаконенная, общепринятая, нормативная группировка.
Метод группировки основывается на двух категориях - группировочном признаке и интервале.
Группировочный признак - это признак, по которому происходит объединение отдельных единиц совокупности в однородные группы. Классификация и группировка должны производиться на основании вполне объективных и легко распознаваемых признаков. При этом последние могут носить как атрибутивный, так и количественный характер. Следует иметь в виду, что в ряде случаев классификация, которая представляется чисто качественной, в конечном итоге оказывается основанной на количественном признаке. Такова, например, классификация промышленных предприятий по отраслям. Поскольку одно и то же предприятие выпускает продукцию разных видов, статистика решает этот вопрос по количественному преобладанию того или иного вида.
Интервал очерчивает количественные границы групп. Как правило, он представляет собой промежуток между максимальными и минимальными значениями признака в группе.
Интервалы бывают:
а) равные, когда разность между максимальным и минимальным значениями в каждом из интервалов одинакова;
б) неравные, когда, например, ширина интервала постепенно увеличивается, а верхний интервал часто не закрывается вовсе;
в) открытые, когда имеется только либо верхняя, либо нижняя
граница;
г) закрытые, когда имеются и нижняя, и верхняя границы.
Остановимся подробнее на группировках по количественному признаку (табл. 4.1).
При непрерывном характере вариации группировочного признака, когда в определенных пределах признак может принимать значение (целое или дробное), весь диапазон изменения признака также разбивается на интервалы. Для группировки использован непрерывный признак (табл. 4.1). группы банков по объявленным уставным фондам отмечены с помощью неравных интервалов, у которых разности между верхней и нижней границами неодинаковы в разных группах. Так, во второй группе величина интервала равна 400 млн. руб., в третьей – 500 млн. руб., в четвертой – 4000 млн. руб., т.е. в приведенной группе величина интервала постепенно увеличивается, а в последней группе верхняя граница не указывается совсем. Интервалы, в которых указана лишь одна граница (верхняя или нижняя), называются открытыми.
Таблица 4.1
Распределение коммерческих банков по объявленным уставным фондам
| Группы коммерческих банков по объявленным уставным фондам, млн. руб. | Количество коммерческих банков, в % к итогу | |
| на 01.03.2005 г. | на 01.03.2006 г. | |
| До 100 | 10,1 | 3,4 |
| 100 - 500 | 64,7 | 42,3 |
| 500 - 1000 | 14,1 | 14,8 |
| 1000 - 5000 | 9,3 | 31,4 |
| 5000 и более | 1,8 | 8,1 |
| ИТОГО |
В приведенном примере открытыми являются первый (указана верхняя граница) и последний интервалы (указана нижняя граница), остальные интервалы являются закрытыми, так как в них указаны и верхняя, и нижняя границы. Неравные интервалы применяются при группировках, которые охватывают массу единиц совокупности с неравномерными и значительными колебаниями признака.
Статистические группировки и классификации преследуют цели выделения качественно однородных совокупностей, изучения структуры совокупности, исследования существующих зависимостей. Каждой из этих целей соответствует особый вид группировки: типологичекая, структурная, аналитическая (факторная).
Типологическая группировка решает задачу выявления и характеристики социально-экономических типов (частных подсовокупностей).
Структурная дает возможность описать составные части совокупности или строение типов, а также проанализировать структурные сдвиги. Аналитическая (факторная) группировка позволяет оценивать связи между взаимодействующими признаками.
В зависимости от числа положенных в их основание признаков различают простые и многомерные группировки.
Группировка, выполненная по одному признаку, называется
простой.
Многомерная группировка производится по двум и более признакам. Частным случаем многомерной группировки является комбинационная группировка, базирующаяся на двух и более признаках, взятых во взаимосвязи, в комбинации.
По отношениям между признаками выделяют иерархические и неиерархические группировки. Иерархические группировки выполняются по двум и более признакам, при этом значения второго признака определяются областью значений первого (например, классификация отраслей промышленности по подотраслям).
Неиерархические группировки строятся, когда строгой зависимости значений второго признака от первого не существует.
Среди простых группировок особо выделяют ряды распределения.
Ряд распределения - это группировка, в которой для характеристики групп (упорядоченно расположенных по значению признака) применяется один показатель - численность группы. Другими словами, это ряд чисел, показывающий, как распределяются единицы некоторой совокупности по изучаемому признаку.
Ряды, построенные по атрибутивному признаку, называются атрибутивными рядами распределения.
Ряды распределения, построенные по количественному признаку, называются вариационными рядами.
По очередности обработки информации группировки бывают первичные (составленные на основе первичных данных) и вторичные, являющиеся результатом перегруппировки ранее уже сгруппированного материала.
Относительно временного критерия группировки бывают статические, дающие характеристику совокупности на определенный момент времени или за определенный период, и динамические. Последние - это группировки, показывающие переходы единиц из одних групп в другие (а также вход и выход из совокупности). Количества таких переходов, рисующие внутреннюю динамику совокупности, удобно располагать в «шахматную» таблицу, которую называют матрицей перехода. Такую матрицу также часто называют миграционной или матрицей мобильности.
Date: 2015-07-27; view: 395; Нарушение авторских прав