
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

ББК С6.я7 2 page
|
|
2.4. Расчет средних по результатам группировки.
Очень часто исходные данные для анализа бывают представлены в сгруппированном виде, когда для каждого значения осредняемого признака Х сообщается частота его повторения. В этих случаях средняя величина рассчитывается по обычным формулам средних взвешенных (арифметических либо гармонических). Сложности возникают, когда в сгруппированных данных указывается не конкретное значение признаках по каждой группе, а лишь интервал его изменения. В данном случае правильный расчет общей средней величины возможен, если каким-либо способом удается получить среднее значение признака по каждой группе; далее используются обычные формулы средних взвешенных. Если же средние значения признака в группах определить по имеющимся сведениям нельзя, то их заменяют серединами интервалов, получая в итоге некоторое, чаще всего вполне удовлетворительное, приближение к среднему значению.
Таким образом, расчет средней арифметической делают по формуле
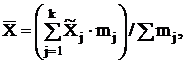 где
где

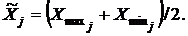
Отметим, что расчет среднего значения по данным группировки требует особого внимания при выборе взвешивающего показателя. Очень часто величины 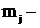 частоты повторения признака Х в исходных данных либо отсутствуют, либо не столь очевидны. Для примера рассмотрим данные таблицы 2.5.
частоты повторения признака Х в исходных данных либо отсутствуют, либо не столь очевидны. Для примера рассмотрим данные таблицы 2.5.
Таблица 2.5.
Основные показатели производительности предприятий
| Группы пред-приятий | Себестоимость одного изделия, тыс.руб. | Число пред-приятий, % | Объем продукции, % | Затраты на производство, % |
| 110—115 | 8,2 | |||
| 115—120 | 17,2 | |||
| 120—125 | 23,9 | |||
| 125 и выше | 50,7 | |||
| Итого | — |
Если с определением середин интервалов никаких сложностей не возникает (112,5; 117,5; 122,5; 127,5), то при назначении взвешивающего показателя типичной ошибкой является выбор признака «Число предприятий». Умножение величины себестоимости одного изделия на число предприятий никакого экономического смысла не имеет, в то время как умножение себестоимости одного изделия на объем продукции дает реальную экономическую величину — общую сумму затрат. Таким образом, в качестве взвешивающего показателя следует выбрать показатель объема продукции. Тогда средняя себестоимость изделия будет равна
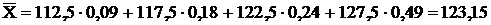 тыс. руб.
тыс. руб.
Частоты повторения признака могут потребовать и применения формулы средней гармонической. Так, показатель «Затраты на производство» в форме относительных величин позволяет также определить среднюю себестоимость изделия:
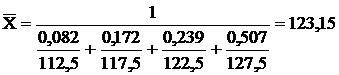 тыс. руб.
тыс. руб.
2.5. Структурные средние
Особый вид средних величин – структурные средние – применяется для изучения внутреннего строения рядов распределения значений признака, а также для оценки средней величины (степенного типа), если по имеющимся статистическим данным ее расчет не может быть выполнен (например, если бы в рассмотренном примере отсутствовали данные и об объеме производства, и о сумме затрат по группам предприятий).
В качестве структурных средних чаще всего используют показатели моды – наиболее часто повторяющегося значения признака – и медианы– величины признака, которая делит упорядоченную последовательность его значений на две равные по численности части, В итоге у одной половины единиц совокупности значение признака не превышает медианного уровня, а у другой – не меньше его.
Если изучаемый признак имеет дискретные значения, то особых сложностей при расчете моды и медианы не бывает. По данным табл. 2.6 определим моду и медиану по тарифному разряду рабочих.
Таблица 2.6
Распределение рабочих по разрядам
Тарифный
разряд
рабочего 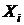
| Число рабочих,
имеющих
соответствующий разряд
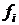
| Частость
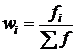
| Накопленная частота
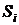
|
| 0,05 | |||
| 0,25 | |||
| 0,40 | |||
| 0,20 | |||
| 0,10 | |||
| ИТОГО |  20 20
| 1,0 | – |
В отличие от средней арифметической, рассчитываемой на основе использования всех вариантов значений признака, мода и медиана характеризует величину варианта, занимающего определенное положение в ранжированном вариационном ряду. Для определения медианы необходимо:
1) построить ряд значений признака в возрастающем порядке (ранжировать), с учётом повторений признака:
2;3;3;3;3;3;4;4;4;4;4;4;4;4;5;5;5;5;6;6;
2) определить номер той единицы, значение признака у которой будет соответствовать медиане:
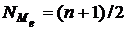 ,
,
где 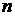 – число единиц в совокупности.
– число единиц в совокупности.
Используя данные табл. 2.6 получим:
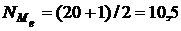 ,
,
т.е. медиана равна средней арифметической из 10-го и 11-го значений признака: (4+4)/2=4. Следовательно медиана равна 4 разряду. Второй вариант определения медианы в дискретных рядах значений признака – по накопленным частотам. Так как 10-я и 11-я единицы ряда имеют величину признака, равную четвертому разряду, т.е. медиана равна четвертому разряду.
Мода для данного ряда распределения также равна четвертому разряду, так как этому разряду соответствует максимальная частота, равная 8.
Если же данные о значениях признака Х представлены в виде упорядоченных интервалов его изменения (интервальных рядов), расчет моды и медианы несколько усложняется необходимостью выбора соответствующего интервала для определения моды и медианы.
Таблица 2.7
Распределение банка по размеру прибыли
| Размер прибыли | Число банков
(частота)
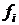
| Накопленная частота
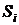
|
| 3,7 – 4,6 | ||
| 4,6 – 5.5 | ||
| 5.5 – 6.4 | ||
| 6,4 –7.3 | ||
| 7.3 – 8,2 | ||
| ИТОГО | 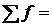 20 20
| – |
Используем данные табл. 2.7, для расчета медианы выбирается интервал, которому соответствует накопленная частота 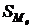 >
> 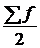 . Таким интервалом является 5.5 – 6.4. Поскольку медианное значение делит всю совокупность на две равные по численности части, оно оказывается в данном конкретном интервале значений признака X. С помощью интерполяции в этом медианном интервале находят значение медианы по формуле:
. Таким интервалом является 5.5 – 6.4. Поскольку медианное значение делит всю совокупность на две равные по численности части, оно оказывается в данном конкретном интервале значений признака X. С помощью интерполяции в этом медианном интервале находят значение медианы по формуле:
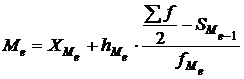 ,
,
где 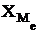 – нижняя граница медианного интервала;
– нижняя граница медианного интервала; 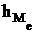 – его величина;
– его величина;
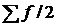 – половина от общего числа наблюдений или половина объема того показателя, который используется в качестве взвешивающего в формулах расчета средней величины (в абсолютном или относительном выражении);
– половина от общего числа наблюдений или половина объема того показателя, который используется в качестве взвешивающего в формулах расчета средней величины (в абсолютном или относительном выражении);
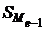 – сумма наблюдений (или объема взвешивающего признака), накопленная до начала медианного интервала;
– сумма наблюдений (или объема взвешивающего признака), накопленная до начала медианного интервала; 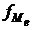 – число наблюдений или объем взвешивающего признака в медианном интервале (также в абсолютном либо - относительном выражении).
– число наблюдений или объем взвешивающего признака в медианном интервале (также в абсолютном либо - относительном выражении).
В нашем примере медиана равна:
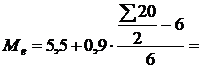 6,1 млн. руб.
6,1 млн. руб.
Таким образом, 50% банков имеют прибыль менее,1 млн. руб., а 50% банков – более 6.1 млн. руб.
При расчете модального значения признака по данным интервального ряда надо обращать внимание на то, чтобы интервалы были одинаковыми, поскольку от этого зависит показатель повторяемости значений признака X. Выбираем интервал обладающий наибольшей частотой повторения признака: 5,5 – 6,4, т.е. мода должна находиться в этом интервале. Для интервального ряда с равными интервалами величина моды определяется как
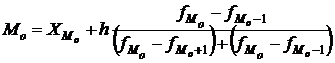 ,
,
где 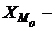 нижнее значение модального интервала;
нижнее значение модального интервала; 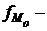 частота соответствующая модальному интервалу или объем взвешивающего признака в модальном интервале (в абсолютном либо относительном выражении);
частота соответствующая модальному интервалу или объем взвешивающего признака в модальном интервале (в абсолютном либо относительном выражении);
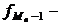 предмодальная частота;
предмодальная частота; 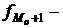 послемодальная частота;
послемодальная частота; 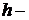 модальный интервал.
модальный интервал.
Величину моды определяем по данным табл. 2.7:
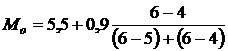 =6,1 млн. руб.
=6,1 млн. руб.
Таким образом, чаще всего встречаются банки с размером прибыли 6.1 млн. руб.
2.5. Показатели вариации
Вариация, т.е. несовпадение уровней одного и того же показателя у разных объектов, имеет объективный характер и помогает познать сущность изучаемого явления.
Для измерения вариации в статистике применяют различные абсолютные и относительные показатели. К абсолютным показателям вариации относятся размах колебаний, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение.
хнесколько способов.
Размах колебаний, или размах вариации, представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности:
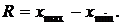
Достоинством данного показателя является простота расчёта. Однако размах вариации зависит от величины только крайних значений признака. Поэтому область его применения ограничена достаточно однородными совокупностями. В частности на практике он находит применение в предупредительном контроле качества продукции.
Точнее характеризует вариацию признака показатель, основанный на учете колеблемости всех значений признака. Поскольку средняя арифметическая является обобщающей характеристикой свойств совокупности, большинство показателей вариации основано на рассмотрении отклонений значений признака. Поскольку средняя арифметическая является обобщающей характеристикой свойств совокупности, большинство показателей вариации основано на рассмотрении отклонений значений признака отдельных единиц совокупности от этой величины. К этим показателям относятся среднее линейное отклонение, дисперсия и среднее квадратическое отклонение представляющее собой среднюю арифметическую из отклонений индивидуальных значений признака от общей средней по совокупности.
Формулы для расчета абсолютных показателей вариации приведены в табл. 2.8.
Таблица 2.8
Формулы расчета абсолютных показателей вариации
| Показатель | По несгруппированным данным | По сгруппированным данным |
1. Среднее линейное отклонение 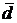 е е
| 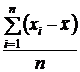
| 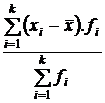
|
2. Дисперсия 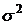
| 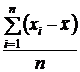
| 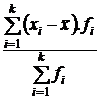
|
| 2а. Преобразованная формула для расчета дисперсии | 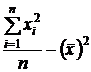
| 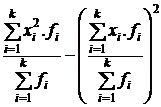
|
3. Среднее квадратическое отклонение 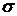
| 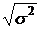
|
В таблице 2.8 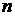 – количество единиц совокупности,
– количество единиц совокупности, 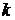 – количество групп, на которые разбита совокупность;
– количество групп, на которые разбита совокупность; 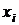 – варианты значений признака по группе
– варианты значений признака по группе 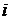 ;
; 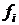 – частота повторения данного варианта.
– частота повторения данного варианта.
При сравнении колеблемости различных признаков в одной и той же совокупности или же при сравнении колеблемости одного и того же признака в нескольких совокупностях с различной величиной средней арифметической пользуются относительными показателями вариации. Эти показатели вычисляются как отношение абсолютных показателей вариации к соответствующей характеристике центра распределения – средней арифметичсекой или медиане. Наиболее часто применяется показатель относительной колеблемости – коэффициент вариации.
Коэффициент вариации рассчитывается по формуле
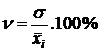 ,
,
где 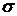 – дисперсия;
– дисперсия; 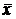 – общее среднее значение признака.
– общее среднее значение признака.
Его используют не только для сравнительной оценки вариации разных признаков или в различных совокупностях, но и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%.
Применим коэффициент вариации для сравнительной оценки колеблемости одного признака в разные периоды времени. Например, проводится анализ вариации цен 1 м  муниципального жилья в разных районах Москвы в январе и мае 2006 г.Известно, что в январе среднее квадратическое отклонение составило 0,7603 тыс. руб., а в мае – 0,9754 тыс. руб. Означает ли это, что в мае возросла вариация цен на муниципальное жилье в Москве? Если принять во внимание, что
муниципального жилья в разных районах Москвы в январе и мае 2006 г.Известно, что в январе среднее квадратическое отклонение составило 0,7603 тыс. руб., а в мае – 0,9754 тыс. руб. Означает ли это, что в мае возросла вариация цен на муниципальное жилье в Москве? Если принять во внимание, что 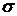 рассчитывается по отклонениям от соответствующей средней арифметической, нужно сопоставить средний уровень цен на муниципальное жильё в Москве за январь и май 2006 г. в январе средняя цена 1 м
рассчитывается по отклонениям от соответствующей средней арифметической, нужно сопоставить средний уровень цен на муниципальное жильё в Москве за январь и май 2006 г. в январе средняя цена 1 м 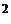 муниципального жилья составляла 38,8 тыс. руб., а в мае – 58,2 тыс. руб. следовательно, вывод об увеличении или вариации цен на муниципальное жильё в мае 2006 г. может быть сделан после расчета показателя относительной колеблемости уровня признака, т.е. коэффициента вариации.
муниципального жилья составляла 38,8 тыс. руб., а в мае – 58,2 тыс. руб. следовательно, вывод об увеличении или вариации цен на муниципальное жильё в мае 2006 г. может быть сделан после расчета показателя относительной колеблемости уровня признака, т.е. коэффициента вариации.
Расчет коэффициента вариации цены 1 м 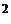 муниципального жилья в Москве приводит к следующим результатам:
муниципального жилья в Москве приводит к следующим результатам:
в январе 2006 г. 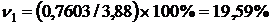 ;
;
в мае 2006 г. 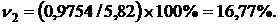
следовательно, в мае 2006 года вариация цен 1 м  муниципального жилья в Москве снизилась по сравнению с январем 2006 года. Поскольку
муниципального жилья в Москве снизилась по сравнению с январем 2006 года. Поскольку
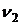 <
< 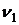 .
.
Если рассчитать дисперсию признака по всей изучаемой совокупности, т.е. общую дисперсию 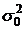 , то полученный показатель будет характеризовать вариацию признака как результат влияния всех факторов, определяющих индивидуальные различия единиц совокупности. Если же поставить задачу – выделить в составе общей дисперсии ту часть, которая обусловлена влиянием какого-либо определенного фактора, то следует разбить изучаемую совокупность на группы. Положив в основание группировки интересующий нас фактор.
, то полученный показатель будет характеризовать вариацию признака как результат влияния всех факторов, определяющих индивидуальные различия единиц совокупности. Если же поставить задачу – выделить в составе общей дисперсии ту часть, которая обусловлена влиянием какого-либо определенного фактора, то следует разбить изучаемую совокупность на группы. Положив в основание группировки интересующий нас фактор.
Затем нужно изучить раздельно вариацию признака в величине признака от группы к группе. Выполнение такой группировки позволяет разложить общую дисперсию признака на две дисперсии, одна из которых будет характеризовать часть вариации, обусловленную влиянием фактора, положенного в основу группировки, а вторая – вариацию,. происходящую под влиянием прочих факторов (кроме фактора, положенного в основу группировки).
Вариацию, обусловленную влиянием фактора, положенного в основу группировки, характеризует межгрупповая дисперсия 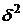 . Которая является мерой колеблемости частных средних по группам
. Которая является мерой колеблемости частных средних по группам 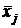 вокруг общей средней
вокруг общей средней 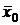 и исчисляется по формуле
и исчисляется по формуле
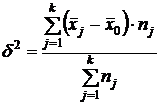 ,
,
где 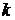 – число групп;
– число групп; 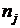 – число единиц в
– число единиц в 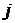 -й группе;
-й группе; 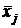 – частная средняя по
– частная средняя по 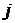 -той группе;
-той группе; 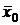 – общая средняя по совокупности единиц.
– общая средняя по совокупности единиц.
Вариацию, обусловленную влиянием прочих факторов, характеризует в каждой группе внутригрупповая дисперсия
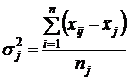 .
.
По совокупности в целом вариация значений признака под влиянием прочих факторов характеризуется средней внутригрупповой дисперсией:
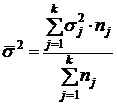 .
.
Между общей дисперсией 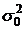 , средней внутригрупповой дисперсией
, средней внутригрупповой дисперсией 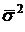 и межгрупповой дисперсией
и межгрупповой дисперсией 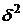 существует соотношение, определяемое правилом сложения дисперсий. Согласно этому правилу общая дисперсия равна сумме средней внутригрупповой и межгрупповой дисперсии:
существует соотношение, определяемое правилом сложения дисперсий. Согласно этому правилу общая дисперсия равна сумме средней внутригрупповой и межгрупповой дисперсии:
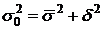 .
.
Рассмотрим правило сложения дисперсий на следующем примере. По результатам маркетингового исследования туристических фирм, организующим недельные туры в Испанию в различные курортные города, получены следующие данные о вариации стоимости туров в сентябре месяце (табл. 2.9).
Таблица 2.9
Группировка туристических фирм по сегментам рынка в Испании
| Местоположение курорта | Число туристических фирм, 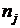
| Средняя цена недельного тура, долл., 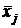
| Дисперсия цен тура в группе, 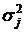
|
| Коста-Брава | 528,57 | 2728,04 | |
| Коста-дель-Соль | 588,33 | 8851,14 | |
| ИТОГО | 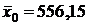
| 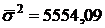
|
Вариация цен в обследованной группе туристических фирм обусловленная различиями в местоположении курорта, будет характеризоваться величиной межгрупповой дисперсии. Средняя цена недельного тура по всем фирмам
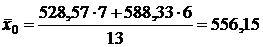 долл.
долл.
Тогда межгрупповая дисперсия
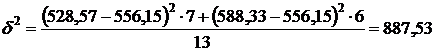 .
.
Вариация цен под влиянием всех прочих факторов, кроме местоположения курорта, будет характеризоваться средней внутригрупповой дисперсией
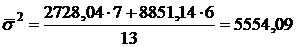 .
.
Вариация цен на недельные туры в Испанию, обусловленная влиянием всех факторов, формирующих уровень цен в данной группе, состоящей из 13 туристических фирм, определяется величиной общей дисперсии:
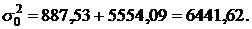
Отсюда можно сделать вывод, что на 13,78% [(887,53/6441,62)×100%] дисперсия цен на недельные туры объясняется различиями в местоположении курорта, а на 86,22% [(5554,09/6441,62)×100%]—влиянием прочих факторов. Таким образом, преобладающее влияние на вариацию цен недельных туров в Испанию оказывают прочие факторы.
Но наряду с вариацией количественных признаков может ставиться задача оценки вариации качественных признаков. При наличии двух взаимоисключающих вариантов значений признака говорят о наличии альтернативной изменчивости качественных признаков. Например, при изучении качества изготовленной продукции можно разделить её на две группы: годную и бракованную. В таком случае оценивается альтернативный признак. Можно считать, что эквивалентом качественного признака будет переменная, которая принимает значения 1 или 0, причем значение 1 она принимает в том случае, когда обследуемая единица обладает данным признаком, а значение 0, когда не обладает им.
Допустим общее число единиц совокупности равно 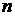 , число единиц, обладающих данным признаком, —
, число единиц, обладающих данным признаком, — 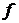 , тогда число единиц, не обладающих данным признаком, будет равно
, тогда число единиц, не обладающих данным признаком, будет равно 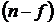 . Учитывая изложенное, построим ряд распределения по качественному признаку (табл. 2.10):
. Учитывая изложенное, построим ряд распределения по качественному признаку (табл. 2.10):
Таблица 2.10
Ряд распределения по качественному признаку
| Значение переменной | Частота повторений |
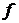
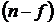
| |
| ИТОГО | 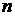
|
Средняя арифметическая такого ряда
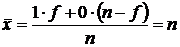 ,
,
т.е. равна относительной частоте (частости), которую можно обозначить через 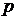 , тогда
, тогда 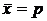 .
.
Таким образом, доля единиц, обладающих данным признаком, равна 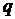 ;
; 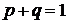 . Тогда дисперсия альтернативного признака определяется по формуле
. Тогда дисперсия альтернативного признака определяется по формуле
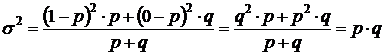 ,
,
а среднее квадратическое отклонение альтернативного признака:
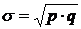 .
.
Например, по результатам контроля качества при приёмке из 1000 готовых изделий 20 оказались бракованными. Применяя вышеуказанную символику, строим ряд распределения (1 соответствует бракованным изделиям, а 0 — годной продукции, табл. 2.11).
Таблица 2.11
Ряд распределения по результатам контроля качества бракованной продукции
| Значение переменной | Частота повторений |
| ИТОГО |
Доля брака по данным равна 2% (20/1000×100%). Тогда величина дисперсии составит 0,0196 (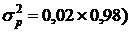 ,а среднее квадратическое отклонение
,а среднее квадратическое отклонение 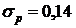 .
.
3. СТАТИСТИЧЕСКОЕ НАБЛЮДЕНИЕ
3.1. Основные этапы статистического исследования
На первом этапе статистического исследования формируются первичные статистические данные, или исходная статистическая информация, которая является фундаментом будущего статистического задания.
Статистическое наблюдение дает исходный материал для обобщения, началом которого служит сводка. На этой стадии совокупность делится по признакам различия и объединяется по признакам сходства, подсчитываются суммарные показатели по группам в целом. С помощью группировок ограничивают качественно однородные в существенном отношении совокупности, что является предпосылкой для определения и применения обобщающих показателей.
На заключительном этапе анализа с помощью обобщающих показателей рассчитываются относительные и средние величины, дается сводная оценка вариации признаков, характеризуется динамика явлений, применяются индексы, балансовые построения, рассчитываются показатели, характеризующие тесноту связей в изменении признаков. С целью наиболее рационального и наглядного изложения цифрового материала он представляется в виде таблиц и графиков.
3.2. Статистическое наблюдение – первый этап статистического исследования
Не всякий сбор сведений является статистическим наблюдением. О статистическом наблюдении можно говорить лишь тогда, когда изучаются статистические закономерности, т. е. такие, которые появляются только в массовом процессе, в большом числе единиц какой-то совокупности. Поэтому статистическое наблюдение должно быть планомерным, массовым и систематическим.
Планомерность статистического наблюдения заключается в том, что оно готовится и проводится по разработанному плану, который включает вопросы методологии, организации, техники сбора информации, контроля за качеством собранного материала, его достоверности, оформления итоговых результатов. Массовыйхарактер статистического наблюдения предполагает, что оно охватывает большое число случаев проявления данного процесса, достаточное для того, чтобы получить правдивые статистические данные, характеризующие не только отдельные единицы, но и всю совокупность в целом. Систематичность статистического наблюдения определяется тем, что оно должно проводиться либо систематически, либо непрерывно, либо регулярно.
Из сказанного следует, что к статистическому наблюдению предъявляются следующие требования:
а) полноты статистических данных (полноты охвата единиц изучаемой совокупности, сторон того или иного явления, а также полноты охвата времени);
Date: 2015-07-27; view: 727; Нарушение авторских прав