
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

ББК С6.я7 1 page
|
|
Министерство образования Российской Федерации
Южно-Уральский государственный университет
Кафедра «Бухгалтерский учет и финансы»
C6.я7
С138
О.В. Сагай
СТАТИСТИКА
Учебное пособие
Челябинск
Издательство ЮУрГУ
ББК С6.я7
Сагай О.В. Статистика: Учебное пособие. – Челябинск: Изд-во ЮУрГУ, 2007. – 44 с.
Учебное пособие содержит основные разделы курса «Статистика». Курс включает: теорию статистики (развитие статистики, методы сбора и обработки данных, анализа статистических взаимосвязей).
Предложенные методики расчета позволяют закрепить лекционный материал по дисциплине «Статистика». Учебное пособие предназначено для студентов, обучающихся по специальности 060500 –«Бухгалтерский учет, анализ и аудит» и является базовым для студентов всех специальностей и форм обучения.
Список лит. – 4 назв.
Одобрено учебно-методической комиссией факультета коммерции.
Рецензенты: С.Б. Ивлев, М.М. Янахова.
ã Издательство ЮУрГУ, 2007.
ВВЕДЕНИЕ
В современных условиях органы государственного и муниципального управления постепенно приходят к осознанию необходимости опоры на статистическую информацию для повышения качества управленческих решений. Субъектам малого и среднего бизнеса необходимы аналитические материалы о состоянии товарных рынков, результатах маркетинговых исследований и т. д.
Знание основных статистических показателей является необходимым условием анализа социально-экономических процессов.
Учебное пособие охватывает раздел курса "Статистика", являющегося одним из основных: теория статистики (развитие анализа статистических взаимосвязей). В дальнейшем на базе курса "Статистика" изучаются конкретные статистические дисциплины, например, анализ хозяйственной и финансовой деятельности, экономика торгового предприятия и др. Что касается специальности 060500 "Бухгалтерский учет, анализ и аудит", данный курс служит основой для разработки и совершенствования методов экономического анализа.
Цель курса – дать представление о содержании статистики как научной дисциплины, познакомить с её основными понятиями, методологией и методиками расчета важнейших статистических аналитических показателей.
1. ОПРЕДЕЛЕНИЕ И ОСНОВНЫЕ ПОНЯТИЯ СТАТИСТИКИ
Слово "статистика" происходит от латинского status – состояние. В науку этот термин ввёл немецкий ученый Готфрид Ахенваль в 18 веке, однако статистический учет существовал уже в глубокой древности: известно, что еще за 5 тыс. лет до н.э. проводились переписи населения в Китае, осуществлялось сравнение военного потенциала разных стран, велся учет имущества граждан в Древнем Риме, затем – населения, домашнего имущества, земель в средние века.
В 19 веке получило развитие учение бельгийского статистика А. Кетле, основоположника учения о средних величинах.
Прогрессу статистической методологии в этом столетии способствовали работы представителей английской математической школы, в России – труды земских статистиков.
Развитие статистической науки, расширение сферы практической работы привели к изменению содержания самого понятия "статистика". В настоящее время данный термин употребляется в трёх значениях:
1) статистика – отрасль практической деятельности, цель которой: сбор, обработка, анализ и публикация массовых данных о самых различных явлениях общественной жизни (в этом смысле "статистика" выступает как синоним словосочетания "статистический учет");
2) статистикой называется цифровой материал, служащий для характеристики какой-либо области общественных явлений или территориального распределения какого-либо показателя;
3) статистикой называется отрасль знания, особая научная дисциплина и соответственно учебный предмет в высших и средних специальных заведениях.
Предметом статистикиявляется количественная сторона массовых общественных явлений в неразрывной связи с их качественной стороной, или их содержанием, а также количественное выражение закономерностей общественного развития в конкретных условиях места и времени.
Свой предмет статистика изучает при помощи определенных категорий, т. е. понятий, которые отражают наиболее общие и существенные свойства, признаки, связи и отношения предметов и явлений объективного мира.
В статистике таких основных понятий пять.
1. Статистическая совокупность– это совокупность социально-экономических объектов или явлений общественной жизни, объединенных качественной основой, общей связью, но отличающихся друг от друга отдельными признаками. Например: совокупность семей, предприятий, форм, объединений и т.п. совокупности могут быть однородными и разнородными.
Однородная совокупность – если один или несколько изучаемых существенных признаков её объектов являются общими для всех единиц. Совокупность оказывается однородной именно с точки зрения этих признаков.
Совокупность, в которую входят явления разного типа, считается разнородной. Совокупность может быть однородна в одном отношении и разнородна в другом. В каждом отдельном случае однородность совокупности устанавливается путем проведения качественного анализа, выяснения содержания изучаемого общественного явления.
2. Единица совокупности – это первичный элемент статистической совокупности, являющийся носителем признаков, подлежащих регистрации, и основой ведущегося при обследовании счета.
3. Признак – это качественная особенность единицы совокупности. Признаки бывают:
признаки, имеющие непосредственное количественноевыражение, например возраст, стаж работы, средний заработок и т.д. они могут быть дискретными и непрерывными;
признаки, не имеющие непосредственного количественного выражения. В этом случае отдельные единицы совокупности различают своим содержанием (например, профессии – характером труда: учитель, столяр, швея-мотористка и т.д.) такие признаки обычно называют атрибутивными (в философии "атрибут" - неотъемлемое свойство предмета). В случае, когда имеются противоположные по значению варианты признака, говорят об альтернативном признаке (да, нет). Например, продукция может быть годной или бракованной (не годной); для представителей отдельных возрастных групп существует вероятность дожить или не дожить до следующей возрастной группы; каждое лицо может состоять в браке или нет и т.д.
Особенностью статистического исследования является то, что в нем изучаются только варьирующие признаки. Т.е. признаки, принимающие различные значения (для атрибутивных, альтернативных признаков) или имеющие различные количественные уровни у отдельных единиц совокупности.
Вариация – это изменение ("колеблемость") величины либо значения признака при переходе от одного объекта (или группы объектов) к другому; точнее говоря – от одной единицы совокупности к другой. Вариация - это изменение величин только в пределах однородной совокупности.
Если же изменения изучаемого явления происходит в разные периоды времени, причем носят характер закономерности, то говорят уже не о вариации признака, а о его динамике.
4. Статистический показатель – это понятие (категория), отображающее количественные характеристики (размеры) соотношения признаков общественных явлений. Статистические показатели могут быть объемными ( численность населения, трудовых ресурсов) и расчетными (средние величины). Они могут быть плановыми, отчетными и прогностическими (т. е. выступать в качестве прогнозных оценок). Статистические показатели следует отличать от статистических данных. Статистические данные– это конкретные численные значения статистических показателей. Они всегда определены не только качественно, но и количественно и зависят от конкретных условий места и времени.
Задачами статистики в этом направлении являются:
а) правильное определение содержания статистического показателя (валового национального продукта, национального дохода, производительности труда и т.п.);
б) разработка методологии подсчета и расчета статистического показателя.
5. Система статистических показателей – это совокупность статистических показателей, отражающая взаимосвязи, которые объективно существуют между явлениями. Для каждой общественно-экономической формации характерна определенная система взаимосвязи общественных явлений. Поэтому образуют систему и статистические показатели.
Система статистических показателей охватывает все стороны жизни общества на различных уровнях: страны, региона – макроуровень; предприятий, фирм, объединений, семей. домохозяйств и т. д. – микроуровень.
Свой предмет статистика изучает при помощи своего, специфического метода. Метод статистики – это целая совокупность приемов, пользуясь которыми статистика исследует свой предмет. Она включает в себя три группы собственно методов: метод массовых наблюдений, метод группировок, метод обобщающих показателей.
1 этап: Статистическое наблюдениезаключается в сборе первичного статистического материала, в научно организованной регистрации всех существенных фактов, относящихся к рассматриваемому объекту.
2 этап: Метод группировок - дает возможностьвсе собранные в результате массового статистического наблюдения факты подвергать систематизации и классификации.
3 этап: Метод обобщающих показателей позволяет характеризовать изучаемые явления и процессы при помощи статистических величин – абсолютных, относительных и средних. На этом этапе статистического исследования выявляются взаимосвязи и масштабы явлений, определяются закономерности их развития, даются прогнозные оценки.
Познавательное значение статистики заключается в том, что:
1) статистика дает цифровое и содержательное освещение изучаемых явлений и процессов, служат самым надежным способом оценки действительности;
2) статистика дает доказательную силу экономическим выводам, позволяет проверить различные утверждения, отдельные теоретические положения;
3) статистика обладает способностью раскрывать взаимосвязь между явлениями, показывать их конкретную форму и силу;
4) статистика первая обнаруживает новые явления, процессы и закономерности, дает их количественную и качественную характеристику.
2. СТАТИСТИЧЕСКЕ ВЕЛИЧИНЫ
2.1. Понятие абсолютной и относительной величины в статистике
Результаты статистического наблюдения регистрируются прежде всего в форме первичных абсолютныхвеличин. Так, основная масса народно-хозяйственных показателей фиксируется в первичных учетных документах. Абсолютная величина отражает уровень развития явления.
С точки зрения конкретного исследования совокупность абсолютных величин можно рассматривать как состоящую из показателей индивидуальных, характеризующих размер признака у отдельных единиц совокупности, и суммарных, характеризующих итоговое значение признака по определенной части совокупности. Так, если индивидуальными будут показатели численности работающих на отдельных предприятиях, то суммарными – численности работающих по группам, объединениям предприятий. С точки зрения отдельного предприятия численность занятых на нём будет суммарной величиной, а численность работающих в каждом цехе – величинами индивидуальными.
Следует разграничивать моментные и интервальные абсолютные величины. Моментные показывают фактическое наличие или уровень явления на определенный момент, дату (например, наличие запасов материалов или оборотных средств, величина незавершенного производства, численность проживающих и т.д.). Интервальные – итоговый накопленный результат за период в целом (объем произведенной продукции за месяц или год, прирост населения за определенный период, величина валового сбора зерна за год и за пятилетку и т.п.). В отличие от моментных интервальные абсолютные величины допускают их последующее суммирование (естественно, если речь идет об одном и том же показателе).
Сама по себе абсолютная величина не дает полного представления об изучаемом явлении, не показывает его структуру, соотношение между отдельными частями, развитие во времени. В ней выявлены соотношения с другими абсолютными показателями. Эти функции выполняют определяемые на основе абсолютных величин относительные показатели.
Относительная величина – это обобщающий показатель, который дает числовую меру соотношения двух сопоставимых абсолютных величин. Так как многие абсолютные величины взаимосвязаны, то и относительные величины одного типа в ряде случаев могут определяться через относительные величины другого типа.
Основное условие правильного расчета относительной величины – сопоставимость сравниваемых показателей и наличие реальных связей между изучаемыми явлениями. Таким образом по способу получения относительные показатели – всегда величины производные, определяемые в форме коэффициентов, процентов, и т.п.
2.2. Виды и взаимосвязи относительных величин
По содержанию выражаемых количественных соотношений выделяют следующие типы относительных величин.
Относительная величина динамики
Характеризует изменение уровня развития какого-либо явления во времени. получается в результате деления уровня признака в определенный период или момент времени на уровень этого же показателя в предшествующий период или момент.
Так, по данным топливно-энергетического баланса России, ресурсы 1993 г. оценивались в 2171, 1 млн. т. у.т. (условного топлива), а 2000 г. – в 2629,1 млн. т. у.т. Относительная величина динамики составила 
i = 2629,1: 2171,1 = 1,211
Таким образом, объем топливно-энергетических ресурсов вырос за 7 лет в 1,211 раза (коэффициент роста, индекс роста, индекс). В процентном выражении это 121,1 % (темп роста).
Иначе говоря, за 7 лет объем ресурсов увеличился на 21,1 % (темп прироста). В среднем каждый год объем ресурсов возрастал по сравнению с предыдущим годом в
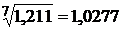
раза или на 2,77 % (среднегодовой коэффициент или индекс роста и среднегодовой темп прироста).
Относительная величина выполнения плана
В планах предприятий задания устанавливаются как в абсолютных показателях, так и в виде относительных величин, которые показывают во сколько Раз или на сколько процентов должна увеличиться (уменьшиться) величина показателя по плану в сравнении с его уровнем в предшествующем периоде. Например, по плану темп роста экспорта продукции предприятия должен был составить в 2002 г. 106,1% (в процентах к предшествующему году), относительная величина динамики – свидетельствует о перевыполнении плана по экспорту продукции предприятия в 2002 г. Степень выполнения плана оценивается с помощью относительной величины выполнения плана, которую получают путём деления фактического уровня показателя в отчетном периоде на его уровень, запланированный на этот же период. Рассчитывается как отношение уровня, запланированного на предстоящий период, к уровню, фактически сложившемуся в предшествующем периоде.
На практике различают две разновидности относительных показателей выполнения плана. В первом случае сравниваются фактические и плановые уровни (таков пример, рассмотренный выше). Во втором случае в плановом задании устанавливается абсолютная величина прироста или снижения показателя и соответственно проверяется степень выполнения плана по этой величине. Так, если планировалось снизить себестоимость единицы продукции на 24,2 руб., а фактическое снижение составило 27,5 руб., то плановое задание по снижению себестоимости выполнено с ростом в 27,5: 24,2 = 1,136 раза, т.е. план перевыполнен на 13,6%. Показатель выполнения плана по уровню себестоимости в данном случае будет меньше единицы. Если фактическая себестоимость изделия равнялась 805,8 руб. при плановой 809,1 руб., то величина выполнения плана составила 805,8: 809,1 = 0,996, или 99,6 %. Фактический уровень затрат на одно изделие оказался на 0,4 % ниже планового.
Относительные величины структуры
Характеризуют долю отдельных частей в общем объеме совокупности, их рассчитывают как отношение числа единиц (или объема признака) в отдельных частях совокупности к общей численности единиц (или объему признака) по всей совокупности.
Относительные величины структуры рассчитываются по сгруппированным данным. Например, в составе промышленно-производственного персонала выделяются четыре категории: рабочие, руководители, специалисты и служащие. Анализ показателей доли (удельного веса) каждой категории промышленно-производственного персонала позволяет сопоставлять состав работников по категориям на различных предприятиях отрасли, в различных отраслях и т.д.
Расчет относительных величин структуры за несколько периодов (табл. 2.1) позволяет выявить структурные сдвиги.
Таблица 2.1
Доля экспорта и импорта в объеме внешнеторгового оборота России
| Год и квартал | Внешнеторговый оборот | В том числе | Удельный вес, % | ||
| экспорт | импорт | экспорта | импорта | ||
| I кв. II кв. III кв. IV кв. | 36,7 37,9 40,4 46,9 | 21,1 20,4 21,6 25,1 | 15,6 17,5 18,8 21,8 | 57,49 53,83 53,47 53,52 | 42,51 46,17 46,53 46,48 |
| Итого за год | 161,9 | 88,2 | 73,7 | 54,48 | 45,52 |
| I кв. II кв. III кв. IV кв. | 36,7 36,4 31,5 28,7 | 18,4 18,7 17,8 19,3 | 18,3 17,7 13,7 9,4 | 50,14 51,37 56,51 67,25 | 49,86 48,63 43,49 32,75 |
| Итого за год | 133,3 | 74,2 | 59,1 | 55,66 | 44,34 |
В табл. 2.1 приведен расчет относительных величин структуры. В них показана доля экспорта и импорта в объеме внешнеторгового оборота России за период с первого квартала 2004 г. по четвертый квартал 2005 г.
Если в 2004 г. доля экспорта во втором, третьем и четвертом кварталах оставалась достаточно устойчивой, то в 2005 г. в первых кварталах наблюдалось снижение доли экспорта по сравнению с 2004 г., а затем, особенно в четвертом квартале, произошло резкое увеличение доли экспорта до 67,25%.Это обстоятельство несомненно связано с резким изменением (почти в три раза) курса доллара.
Относительные величины структуры рассчитываются по сгруппированным данным:
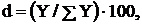
где 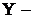 уровень части совокупности;
уровень части совокупности; 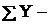 суммарный уровень совокупности.
суммарный уровень совокупности.
Для аналитических расчетов предпочтительнее использовать коэффициентное представление, без умножения на 100.
Относительные величины координации
Относительные величины, характеризующие соотношения двух частей одного целого, называют относительными величинами координации. К таким величинам относятся, например, показатели, характеризующие соотношение численности городского населения, численность рабочих и служащих, величин заемного и собственного капитала банка и т.д. Относительные величины координации нередко характеризуются числом единиц одной части на 100 или 1000 единиц другой части. Например, в 2004 г. на 1000 руб. экспорта приходилось 836 руб. [(73,7 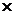 1000)/88,2], а в 2005 г. на каждые 1000 руб. экспорта приходилось уже 796,5 руб. импорта [(59,1
1000)/88,2], а в 2005 г. на каждые 1000 руб. экспорта приходилось уже 796,5 руб. импорта [(59,1 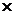 1000)/74,2].
1000)/74,2].
Относительные величины наглядности
Относительные величины, которые отражают результаты сопоставления одноименных показателей, относящихся к одному и тому же периоду (или моменту) времени, но к разным объектам и территориям, называются относительными величинами наглядности. Этот вид относительных величин применяется для сравнительной оценки уровня развития стран и регионов, а также при оценке результатов деятельности отдельных предприятий отрасли.
Таблица 2.2
Потребление некоторых продуктов питания на душу населения, кг
| Год | Страна | Продукты питания | ||||
| мясо | картофель | овощи | фрукты | хлеб | ||
| Россия США | ||||||
| Россия США | ||||||
| Отношение уровня потребления продуктов питания в России к уровню потребления в США | ||||||
| — — | 0,55 0,28 | 1,95 2,34 | 0,77 0,51 | 0,42 0.19 | 1,21 1,35 |
Обычно их исчисляют в процентах или кратных отношениях, показывающих, во сколько раз одна из сравниваемых величин больше (или меньше) другой.  Данные табл. 2.2 свидетельствуют об увеличении разрыва в потреблении в России и США всех приведенных в таблице продуктов питания. Особенно резко отличается потребление мяса и фруктов (соответственно 0,28 и о,19 от уровня США в 2005 году.). В то же время значительно выше уровень потребления в России по сравнению с США таких продуктов, как хлеб и картофель (соответственно 1,35 и 2,34 от уровня США в 2005 году).
Данные табл. 2.2 свидетельствуют об увеличении разрыва в потреблении в России и США всех приведенных в таблице продуктов питания. Особенно резко отличается потребление мяса и фруктов (соответственно 0,28 и о,19 от уровня США в 2005 году.). В то же время значительно выше уровень потребления в России по сравнению с США таких продуктов, как хлеб и картофель (соответственно 1,35 и 2,34 от уровня США в 2005 году).
Относительные величины наглядности находят широкое применение не только при международных сопоставлениях, но при сравнительной оценке показателей деятельности предприятий и различных регионов. Так могут сравниваться результаты работы предприятий различных форм собственности. Безусловный интерес представляет сопоставление цен на продукцию государственных и частных предприятий, средней заработной платы работников этих предприятий.
Относительные величины интенсивности
Отношение между разноименными абсолютными величинами называют относительными величинами интенсивности. В их числе можно назвать показатели уровня жизни населения, к которым относятся приведенные в табл. 2.2 показатели потребления продуктов питания и непродовольственных товаров на душу населения; показатели обеспеченности предметами культурно-бытового и хозяйственного длительного пользования в расчете на 100 семей или 1000 человек населения; показатели обеспеченности населения жильём и т.д. учитывая экономическую сущность относительных величин интенсивности, их можно было бы назвать показателями уровня экономического и социального развития.
Относительными величинами интенсивности выступают, например, показатели выработки продукции в единицу времени, затрат на единицу продукции, трудоёмкости, эффективности использования производственных фондов и т.д., поскольку их получают сопоставлением разноименных величин, относящихся к одному и тому же явлению и одинаковому периоду или моменту времени. Метод расчета относительных величин интенсивности применяется при определении средних уровней (среднего уровня выработки, средних затрат труда, средней себестоимости изделий, средней цены и т.д.). Поэтому распространено мнение, что относительные величины интенсивности – это один из способов выражения средних величин.
2.3. Средние величины
Средняя величина – это обобщающий показатель. Он выражает величину признака, отнесенную к единице совокупности.
Средняя всегда обобщает количественную вариацию признака, т.е. в средних величинах погашаются индивидуальные различия единиц совокупности, обусловленные случайными обстоятельствами.
Средние величины делятся на два больших класса: степенные средние и структурные средние. В практической статистке наибольшее распространение получили следующие виды степенных средних: средняя арифметическая, средняя квадратическая, средняя геометрическая и в качестве структурных средних рассматриваются мода и медиана.
Простая средняя считается по несгруппированным данным и имеет следующий вид:
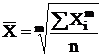 ,
,
где 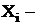 варианта (значение) осредняемого признака;
варианта (значение) осредняемого признака; 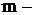 показатель степени средней;
показатель степени средней; 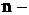 число вариант.
число вариант.
Взвешенная средняя
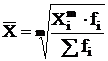 ,
,
где 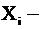 варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта;
варианта (значение) осредняемого признака или серединное значение интервала, в котором измеряется варианта; 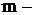 показатель степени средней;
показатель степени средней;
 частота, показывающая, сколько раз встречается i-е значение осредняемого признака.
частота, показывающая, сколько раз встречается i-е значение осредняемого признака.
Для примера рассмотрим данные таблицы 2.3.
Таблица 2.3.
Расчет среднего возраста студентов в группе из 20 человек
| № | Возраст (лет) | № | Возраст (лет) | № | Возраст (лет) | № | Возраст (лет) |
Средний возраст рассчитываем по формуле простой средней
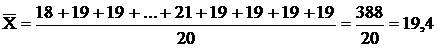 года
года
Сгруппируем исходные данные. Получим следующий ряд распределения:
| Возраст, X лет | Всего | |||||
| Число студентов |
В результате группировки получаем новый показатель – частоту, указывающую число студентов в возрасте X лет.
Следовательно, средний возраст студентов группы будет рассчитываться по формуле взвешенной средней
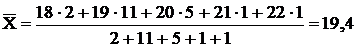
 года.
года.
Общие формулы расчета степенных средних имеют показатель степени (m). В зависимости от того, какое значение он принимает, различают следующие виды степенных средних:
средняя гармоническая, если m = – 1;
средняя геометрическая, если m 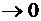 ;
;
средняя арифметическая, если m =1;
средняя квадратическая, если m = 2;
средняя кубическая, если m =3.
Формулы степенных средних приведены в таблице 2.4.
Если рассчитать все виды средних для одних и тех же исходных данных, то значения их окажутся неодинаковыми. Здесь действует правило мажорантности средних: с увеличением показателя степени m увеличивается и соответствующая средняя величина
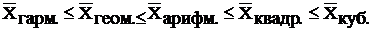
В статистической практике чаще, чем остальные виды средних взвешенных, используются средние арифметические и средние гармонические взвешенные.
Таблица 2.4
Формулы степенных средних
| Вид степенной средней | Показатель степени (m) | Формула расчета | |
| Простая | Взвешенная | ||
| Гармоническая |
–1 
|
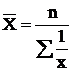
|
 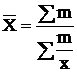
|
| Геометрическая |
 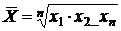
|  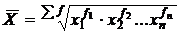
| |
| Арифметическая |
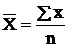
|
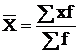
| |
| Квадратическая | 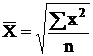
|
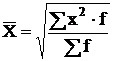
| |
| Кубическая | 
| 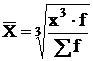
|
Date: 2015-07-27; view: 895; Нарушение авторских прав