Торсионные поля

Вращательное движение всегда удивляло и ставило в тупик исследователей, пытавшихся "копнуть" глубже. Перед ним спасовала даже теория относительности Эйнштейна. При всей его кажущейся простоте и распространённости в природе и технике вращательное движение по сей день остаётся малоизученным и таит в себе загадок не меньше, чем вода. Можно смело сказать, что кто до конца познает вращательное движение, тот познает природу, ибо в природе всё вращается, начиная от элементарных частиц и кончая..., нет, даже не галактиками, которые, как все знают, тоже вращаются и представляют собой гигантские вихри из миллионов звёзд, связанных между собой силами гравитации, а самой Вселенной, которая, оказывается, тоже вращается [9].
Все знают, что когда электрически заряженное тело движется по круговой траектории, то создаётся магнитное поле, направленное вдоль оси обращения заряда. А что создаётся, когда незаряженное тело движется по круговой траектории? Долгое время физики полагали, что ничего. Но вот в 70-е годы XX века некоторые из них (в том числе и русские физики Г. И. Шипов и А. Е. Акимов) начали понимать, что и тут рождается какое-то поле, направленное вдоль оси вращения. Они назвали это поле полем вращения, или торсионным полем. В работах Шипова и Акимова [55,69] было выявлено много удивительных свойств торсионных полей.
Самыми главными из них являются направленность этих полей вдоль оси вращения порождающих их тел и бесконечно большая скорость распространения торсионных полей.
С последним утверждением никак не могли смириться сторонники закостенелых представлений теории относительности. Она ведь постулировала, что в природе нет скоростей распространения чего-либо, превышающих скорость света в вакууме С. И хотя в квантовой механике уже давно было признано существование мгновенных квантовых скачков элементарных частиц на хоть и малые, но конечные расстояния, что фактически означало признание существования бесконечно большой скорости перемещения элементарных частиц на эти расстояния, официальная наука продолжала цепляться за догмы теории относительности и объявлять лженаукой всё, что противоречило им.
Поэтому на разработчиков теории торсионных полей в конце 90-х годов обрушилась лавина ожесточённой и часто необоснованной критики со стороны закостенелых консерваторов. Примером тому может служить статья кандидата физико-математических наук А. Бялко. известного тем, что он вот уже полжизни протирает штаны за круглым столом с рулеткой знаменитого телевизионного Клуба Знатоков [66].
Критиковать было легко, потому что теория торсионных полей, развитая Г. И. Шиповым из общей теории относительности Эйнштейна, настолько сложна и громоздка, что в ней мало кто мог разобраться. А чем запутаннее теория, тем легче её ругать.
И тут наша теория движения, частично изложенная в [ 9 ] и [263], решительно пришла на помощь теории торсионных полей. В [9] нами было убедительно показано, что всякое вращательное движение необходимо считать мнимым в отличие от поступательного движения, считающегося действительным. В самом деле, мы ведь не можем по внешнему виду отличить вращающийся отполированный диск от такого же невращающегося. Мы только можем знать (мнить), что один из них вращается. А если говорить серьёзно, то достаточно указать, что центр вращения при вращении тела на месте не перемещается в пространстве.
Поэтому векторы тангенциальной скорости Vr, импульса Рr и волнового вектора kr вращательного движения следует считать мнимыми величинами и ставить во всех формулах перед символами этих векторов букву
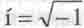,означающую мнимую единицу.
В правильности такого подхода легко убедиться, подставив букву i в выражение для кинетической энергии тела, обращающегося по круговой орбите:

(16.24)

Появившийся здесь знак минуса означает не отрицательность кинетической энергии данного тела, а то, что её надо вычитать из массы-энергии покоя этого тела, когда мы вычисляем его суммарную массу-энергию:

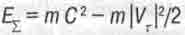(16.25)

Видим, что суммарная масса-энергия вращающегося тела оказывается меньше исходной массы-энергии покоя этого тела на величину Еrкин.
Таким образом, мы сразу получили тот результат, к которому без представления о мнимости вращательного движения шли довольно долгим путём в разделе 16.1. Это доказывает правильность наших представлений о мнимости вращательного движения.
Воодушевлённые этим результатом, попробуем применить представление о мнимости вращательного движения к выводу основного уравнения теории торсионного поля.
В квантовой механике с движением частиц вещества сопоставляются, как известно, волны де Бройля, называемые еще "волнами материи". Они описываются псифункцией

(16.26)

в которой г - радиус-вектор из начала координат до данной точки, t - время от начала движения. Волновой вектор k = P/Ћ здесь рассматривают обычно лишь для частиц, движущихся прямолинейно с импульсом Р. Циклическую частоту волны де Бройля определяют из формулы Планка Е= h , в которой Е- энергия частицы, h - постоянная Планка.
Когда мы хотим описать волну де Бройля для вращающейся или обращающейся материальной частицы, то должны поставить букву i перед волновым вектором в показателе экспоненты формулы (2.26). Отличие всего в одной букве, а как разительно изменяется результат! Ведь если теперь так исправленное выражение расписать по формуле Эйлера и, как это всегда делают с подобными разложениями в электродинамике, учесть только его действительную часть, то получим:

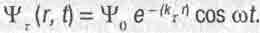(16.27)

Последнее выражение описывает уже не бегущую, а стоячую волну, фаза которой не зависит от r, то есть одинакова во всех точках пространства. А это означает, что такая волна появляется во всех его точках одновременно, то есть распространяется с бесконечно большой скоростью. Такое заключение совпадает с одним из основных свойств торсионных полей, предсказанных Шиповым в [55 ].
Экспоненциальный множитель в (16.27) быстро затухает с расстоянием г по всем направлениям от вращающегося тела, кроме одного направления вдоль оси его вращения, так как здесь скалярное произведение (krr) принимает нулевое значение и экспонента равна единице на любом расстоянии от вращающегося тела. То есть юрсионное поле остронаправлено по оси вращения. А это второе известное свойство торсионных полей. Итак, наша формула (16.27) описывает все основные свойства торсионных полей, вытекающие из теории Шилова. Но у нас всё выводится несравненно проще, нагляднее и доказательнее, чем у Шилова.

Date: 2015-07-27; view: 518; Нарушение авторских прав