Глава шестнадцатаяТЕОРЕТИЧЕСКИЕ ПРЕДПОСЫЛКИ

16.1. Теорема вириала требует энерговыделения при ускорении вращения тел

Теория относительности А. Эйнштейна, освещавшая физикам путь на протяжении XX века и до сих пор считающаяся в официальной физике непогрешимой, утверждает, что с увеличением скорости V поступательного движения тела его масса растёт в соответствии с формулой релятивистского возрастании массы

(16.1)

Здесь С - скорость света в вакууме, m0 - масса покоя тела. Объясняется это возрастание просто: с повышением скорости V тела при ускорении его движения в массу этого тела превращается кинетическая энергия, вкладываемая извне от источника движущей силы. Ведь масса и энергия, согласно теории относительности, -эквивалентные величины и связаны между собой другой известной формулой Эйнштейна

(16.2)

Формула (16.1) была выведена А. Эйнштейном для прямолинейного движения тел. Но многие применяют её, не задумываясь, и для вращательного или обращательного движения. Не задумываются потому, что многочисленные эксперименты с элементарными частицами, ускоренными до околосветовых скоростей в циклических ускорителях, показали, что масса такой частицы, несущейся по круговой траектории в циклотроне, растёт в соответствии с формулой (16.1). Физики учитывают это при расчётах траекторий частиц в ускорителях.
Поэтому многие полагают, что при раскручивании маховика или другого тела или системы связанных тел до больших скоростей вращения их масса должна слегка возрасти в соответствии с формулой (16.1). Правда, при технических скоростях ожидаемое увеличение массы столь мало, что ни на каких весах его не уловить.
Но ошибаются те, кто так думают. Ошибаются не в том, что такое изменение массы трудно измерить, а в том, что масса вращающейся системы тел должна возрасти. Для того чтобы убедиться в этом, давайте вспомним известную всем, кто добросовестно изучал курс механики, теорему вириала, открытую в 1870 г. Р. Клаузиусом. (Кто впервые слышит об этой теореме - пусть не смущается - её не в каждом курсе механики читают студентам, считая, что рядовым механикам и конструкторам она не очень нужна для повседневной работы. Недаром эту теорему вы не найдёте в большинстве известных справочников по физике, изданных для инженеров и студентов.)
Теорема вириала гласит, что ео всякой связанной системе движущихся тел, находящейся в состоянии динамического равновесия, средняя во времени энергия их связи друг с другом по своей абсолютной величине в 2 раза больше средней во времени суммарной кинетической энергии движения этих тел относительно друг друга:

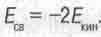(16.3)

Вывести эту формулу очень просто, рассмотрев движение планеты, имеющей массу m, вокруг звезды с массой М. На планету действует центробежная сила, стремящаяся отбросить её от звезды:

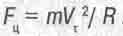(16.4)

(Здесь R- радиус орбиты, Vr - тангенциальная скорость движения планеты по орбите.)
Центробежной силе противодействует сила гравитационного притяжения планеты к звезде:

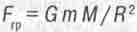(16.5)

(Здесь G- гравитационная постоянная, измеренная ещё в 1789 г. лордом Кельвином.)
Составим теперь уравнение движения для планеты, обращающейся вокруг звезды по равновесной круговой орбите. Такое уравнение, как известно, выражает сумму всех сил, действующих на движущееся тело:

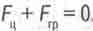(16.6)

Из него следует

(16.7)

Знак минуса здесь означает, что сила гравитационного притяжения направлена противоположно центробежной силе.
Если подставить в последнее равенство значения соответствующих сил - правые части формул (16.4) и (16.5), то получим известное выражение для гравитационного потенциала

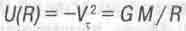(16.8)

Когда планета движется по орбите со скоростью V, она обладает кинетической энергией

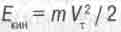(16.9)

А гравитационное взаимодействие планеты со звездой определяет величину энергии гравитационной связи системы звезда-планета

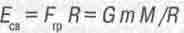(16.10)

Подставив правую часть уравнения (16.8) в формулу (16.9) вместо и учтя выражение (16.10), получим теорему вириала:

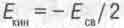(16.11)

Эту теорему хорошо знают астрономы. Используют её и физики, когда вычисляют полную энергию атома, исходя из планетарной модели атома Резерфорда.
Только в атоме вместо гравитационных сил действуют силы электрического притяжения электрона к ядру атома, определяемые законом Кулона:

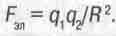(16.12)

А теперь позвольте обратить внимание на знак минуса в уравнении теоремы вириала. Многие в последние годы объясняют этот знак тем, что энергия связи -величина отрицательная. Исходя из этого, большинство астрофизиков всерьёз считают гравитационную энергию отрицательной. Но отрицательных энергий не существует, как и отрицательных масс. Знак минуса в уравнении (16.11) появился лишь потому, что вектор центростремительной силы направлен противоположно вектору центробежной силы. Во времена Клаузиуса физики это хорошо понимали. Поэтому рассматривали лишь абсолютные величины энергий, толкуя теорему вириала.
В те времена она была полезной, пожалуй, только астрономам. Она говорила им, например, что когда кинетическая энергия движения планеты несколько больше половины абсолютной величины энергии гравитационной связи этой планеты с её звездой, то планета переходит с равновесной круговой орбиты на неравновесную эллиптическую. Эллипс орбиты тем вытянутее, чем больше нарушено равенство (16.11). А когда кинетическая энергия возрастает до величины потенциальной энергии связи |Е |, планета или космический летательный аппарат срывается с эллиптической орбиты и уходит в космическое пространство по параболической траектории. Потому-то скорость V, при которой это случается, называют параболической, или второй космической скоростью. А ту, которую тело имело на круговой орбите при

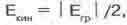(16.13)

называют, как известно, первой космической скоростью.
Эти примеры из области астрономии и космонавтики приведены здесь неслучайно: ведь именно космонавтика, в частности РКК "Энергия" им. С. П. Королёва, ещё в 1994 г. дала теплогенератору Потапова "путёвку в жизнь" - заключение о работоспособности этого аппарата, сделанное на основании всесторонних испытаний (см. приложение, с. 361).
Но вернёмся к вопросу о том, возрастает ли полная масса-энергия системы связанных тел при ускорении её вращения. Так ставить вопрос во времена Клаузиуса никто не мог, ибо тогда люди ещё не знали об эквивалентности массы и энергии, выражаемой формулой (16.2). Мы же, помимо этого, можем учесть ещё, что с увеличением тангенциальной скорости V движения тела по круговой или эллиптической орбите масса этого тела m возрастает по формуле релятивистского возрастания масс (16.1). Подставив выражение (16.1) вместо m в уравнение (16.10), и учтя, что GM/R= - , получим:

(16.14)

где .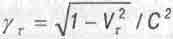
В релятивистской механике кинетическую энергию тела определяют не классической формуле (16.9), а как разность между полной (релятивистской) энергии этого тела Еп = Е0 / у r и его энергией покоя :

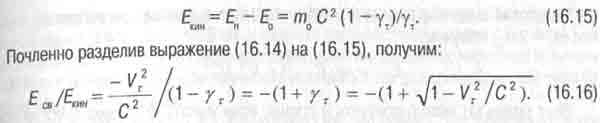
Это соотношение называют релятивистским обобщением теоремы вириала и известно оно ещё с 20-х годов [14].
При технических скоростях вращения тел и даже при космических скоростях движения планет вокруг звёзд квадрат релятивистского фактора ß =Vr/С под знаком радикала в формуле (16.16) исчезающе мал. Поэтому при таких скоростях отношение Eсв/Eкин с большой точностью равно -2, и эта формула превращается в классическое
уравнение теоремы вириала (16.11).
Рассмотрим теперь систему, состоящую из двух тел с массой покоя mlo каждое, связанных между собой гравитационными или кулоновскими силами и обращающихся с тангенциальной скоростью V вокруг их общего центра масс. (Подразумеваем, что расстояние 2R между центрами масс тел много больше их размеров.) В природе такой системе соответствуют двойные звёзды, которых довольно много в небе, и позитроний, состоящий из электрона и позитрона (антиэлектрона), удерживаемых вместе кулоновскими силами и обращающихся вокруг их общего центра масс (пустого места).
В такой системе, как и в предыдущем примере с планетной системой, центробежная сила вычисляется по формуле (16.4). А вот противодействующая ей сила взаимного притяжения двух тел, связывающая их, описывается несколько иной формулой, чем в предыдущем примере, потому что теперь расстояние между этими телами в 2 раза больше радиуса орбиты R. Так, для гравитационной связи между одинаковыми двойными звёздами её вычисляют по формуле

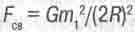(16.17)

По этой же причине гравитационный потенциал, создаваемый одним телом с полной (релятивистской) массой m1 в точке, где находится другое такое же тело этой системы, составляет величину - .
Если подставить величину - 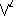вместо выражения, стоящего в правой части последнего уравнения, в формулу для энергии гравитационной связи такой системы 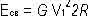и учесть, что m1 = m10 / уr, то получим выражение, совпадающее с (16.14).
Кинетическая же энергия системы сложится из кинетических энергий двух её тел, движущихся с тангенциальной скоростью V. При этом каждую из них будем вычислять о релятивистской формуле (16.15).
определившись со всем этим, теперь можно приступить к вычислению суммарной массы-энергии ЕE такой системы. Она складывается из масс-энергий покоя двух тел , их кинетических энергий Е1кин и только что вычисленной энергии связи:

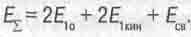(16.18)

Подставив сюда выражения (16.14) и (16.15), а также выражение для E10 и учтя что m0 = 2m1о, получим:

(16.19)

Этот результат можно получить и проще, если учесть, что сумма энергии покоя тела Ео и его кинетической энергии Екин равна, по определению (16.15), полной (релятивистской) энергии этого тела r и если сразу догадаться, что энергию связи надо вычитать из полной энергии системы. Тогда

(16.20)

Получается, что суммарная энергия системы равна её полной (релятивистской) энергии за вычетом энергии связи. Повторяем, это не означает, что энергия связи -отрицательна. Это говорит лишь о том, что энергию связи надо вычитать из суммы всех масс-энергий связанной системы тел при подведении баланса энергий.
А разделив обе части уравнения (16.19) на 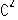, получим искомую формулу для массы вращающейся системы связанных тел:

(16.21)

Последняя формула может, по-видимому, шокировать тех, кто считает, что массы вращающихся тел должны возрастать с увеличением скорости их вращения. Но формулы (16.19) и (16.21) настойчиво утверждают, что они ошибаются: наоборот, суммарная масса-энергия вращающейся системы связанных тел уменьшается с увеличением скорости вращения.
Скептики бросятся искать ошибки в приведенных выкладках. Вряд ли найдут -мы в них не проявляли особой самодеятельности - почти все аккуратно переписано из старых учебников, в том числе из [14]. Может, даже слишком подробно, что делает выкладки чересчур громоздкими. Вот если бы читатель был знаком с нашей теорией движения, изложенной в [8] и предложенной взамен теории относительности, то вывод формулы (16.21) занял бы всего полстраницы. Но теория движения пока мало кому известна, хотя она проще, понятнее и логичнее теории относительности, в которой она, кстати, исправляет ряд грубейших математических ошибок, сделавших теорию относительности противоречивой и беспомощной.
Не найдя ошибок в вышеприведенных выкладках, скептики заявят, что наше утверждение о том, что массы тел при ускорении их вращения должны уменьшаться, ещё не означает, что они действительно уменьшаются у любого тела, приводимого во вращение. Ведь мы сами рассказывали, что системы могут переходить в неравновесное состояние, при котором теорема вириала нарушается и планеты, например, движутся по эллиптическим орбитам. Скептик скажет, что все системы при ускорении их вращения будут переходить в неравновесное состояние (например за счёт упругих деформаций), и мы не сможем доказать, что масса колеса автомобиля уменьшается при ускорении его вращения, ибо ещё не придумали такие точные весы, с помощью которых можно было бы зарегистрировать столь малые изменения массы колеса, которые предсказывает формула (16.21).
Но пусть Вас не смущает то, что уменьшение массы на величину ∆m мы не сможем измерить взвешиванием. Ведь массе Am соответствует энергия ∆Е= ∆m 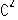.Ta-кая энергия должна уйти из системы, приводимой во вращение, например излучиться А энергию излучений люди научились измерять с несравненно большей чувствительностью, чем массы тел.
Вспомнив уравнение (16.20), Вы, конечно же, догадались, что энергия?Е, излучаемая системой тел при приведении её во вращение, равна изменению энергии связи E между этими телами.
То, что энергия связи действительно излучается из системы тел, между которыми начинает действовать связывающее их притяжение, доказывает пример атома водорода, в котором энергия связи электрона с протоном составляет приблизительно 14 эВ. Столько энергии излучается в виде света в момент образования этого атома из протона и электрона (рекомбинационное излучение). В результате масса атома водорода оказывается меньше суммы масс протона и электрона на величину ∆m = = Есв/ 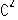, называемую "дефектом массы". Когда же хотят ионизовать атом водорода (разорвать его на протон и электрон), то должны сообщить этому атому извне такое же количество вращательной или колебательной энергии ∆Е ~ 14 эВ, называемой в этом случае энергией ионизации атома.
Теперь Вы, наверно, окончательно поняли, что энергия связи - это не отрицательная энергия, а просто недостача у системы такого количества обычной (положительной) массы-энергии до величины, равной сумме тех масс-энергий отдельных тел, составляющих систему, которыми они обладали до объединения в систему.
Выражение "энергия связи" в наше время широко используется в физике, а еще больше в химии. Но при преподавании химии студентам сплошь и рядом забывают втолковывать, что эта энергия уходит из системы при образовании связи, притом чаще всего уходит в виде электромагнитных излучений (фотонов). Может потому, что плохо втолковывали, теплогенератор Потапова был изобретён лишь в конце XX века, хотя мог появиться ещё в начале века, когда стала понятна связь между массой и энергией, а может быть и раньше - сразу после открытия теоремы вириала.
Но сколько энергии может излучиться из системы связанных тел при ускорении её вращения? На первый взгляд, можно подумать, что эта энергия не превысит разности между массой-энергией Е0 = m0 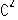данной системы до ускорения её вращения и суммарной массой-энергией ЕE определяемой по формуле (16.19), которой система должна обладать в равновесном состоянии после ускорения её вращения:

(16.22)

Если воспользоваться известной формулой приближённого исчисления 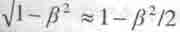[19 ] и подставить правую часть данного выражения вместо радикала в (16.22), а также учесть, что релятивистский фактор ß r = Vr/C, то получим:

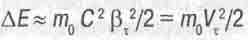(16.23)

В правой части последнего уравнения мы получили не что иное, как классическую формулу (16.9) для кинетической энергии тела, обращающегося с тангенциальной скоростью Vr Уже этот результат, показывающий, что количество излучаемой энергии достигает величины кинетической энергии, вкладываемой во вращение тела может потрясти неподготовленного читателя. Ведь речь шла вроде бы о релятивистских эффектах, а они проявляются, как все привыкли думать, лишь при околосветовых скоростях движения. Формула же (16.23) работает при сколь угодно низких скоростях Vr! Она показывает, что энергии может выделиться не так уж мало -до одного Джоуля излучения на каждый Джоуль энергии, вкладываемой во вращение тела.
Но мы ошиблись. На самом же деле формула (16.23) показывает, что на каждый вкладываемый во вращение тела Джоуль энергии должно выделяться до двух Джоулей внутренней энергии этого тела. Два, а не один, потому, что когда Вы при раскручивании тела добавляете к его исходной массе-энергии ещё один Джоуль кинетической энергии, ускоряя его вращение, а в результате этого суммарная масса-энергия тела уменьшается на один Джоуль по сравнению с исходной, то энергия, уходящая в виде излучения, должна составлять два Джоуля.
Это понятно и из классического уравнения теоремы вириала (16.3), с которого мы начинали наш разговор. Из него непосредственно следует, что изменение энергии связи системы тел при ускорении её вращения должно быть по абсолютной величине в 2 раза большим, чем изменение кинетической энергии вращения этой системы.
Тут сметливый читатель может воскликнуть, что с этого и надо было начинать, а не морочить голову релятивистской механикой. На это ответим, что уравнение (16.3) известно людям уже 130 лет, но никто почему-то до сих пор не делал из него вывода, что ускорение вращения тел должно вести к излучению ими энергии, в 2 раза большей той, которую затрачивают на это ускорение. Потребовалось появление теории движения [ 9 ], чтобы высветить этот вопрос и заострить на нём внимание. Да и рассматривать изменение суммарной массы-энергии системы тел без привлечения формул теории относительности, связывающих массу с энергией, никак нельзя. Поэтому оперировать только с формулами классической механики в данном случае было бы неубедительно.
И вообще выявленный эффект уменьшения массы тел при ускорении их вращения - чисто релятивистский эффект. Ведь классическая теорема вириала только констатировала, что в равновесной системе потенциальная энергия связи её тел должна быть в 2 раза больше кинетической энергии вращения этой системы, но ничего не говорила о необходимости уменьшения массы системы при ускорении ее вращения.
В заключение этого раздела хочется еще раз порадовать читателя, одолевшего всю вышеизложенную математику. Максимальный выигрыш в энергии, который можно получить путем раскручивания тел и превращения части их внутренней энергии в энергию излучений, может достигать не 200, а 300%, ибо после раскручивания и излучения двухсот процентов энергии система продолжает вращаться, сохраняя тот же момент количества движения. Если теперь рекуперировать и использовать энергию её вращения, как энергию инерциального вращения маховика, то мы вернем почти всю кинетическую энергию, вложенную нами ранее в ускорение раскручивания системы (см. рис 4.1.) В результате всего этого система вернётся в исходное состояние, лишь её масса станет чуточку меньше. Но это уменьшение массы в соответствии с формулой Эйнштейна ∆m = ∆Е/ 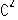столь ничтожно, что чувствительности никаких весов не хватит, чтобы его заметить. Можно будет осуществить миллионы таких циклов ускорения вращения, излучения и торможения, прежде чем расход массы вещества - "топлива" - в таком процессе получения энергии достигнет заметной величины.
Когда автор впервые сделал вышеизложенные расчёты, то написал: "Безусловно, это открывает огромные перспективы перед энергетикой, обещает доселе невиданные источники даровой энергии. И похоже, что это будут экологически чистые и безвредные источники" [ 9 ]. Автор тогда ещё не знал, что такой источник энергии уже изобретен, уже работает и называется вихревым теплогенератором Потапова.

Date: 2015-07-27; view: 629; Нарушение авторских прав