Как излучает синхротрон?

Внимательный читатель, ознакомившись с предыдущим разделом, может спросить: из формулы (16.21) следует, что масса тела при ускорении его движения по круговой траектории должна уменьшаться, почему же в самом начале этого раздела упоминалось о многочисленных экспериментах с элементарными частицами, ускоряемыми на циклических ускорителях, при которых было выявлено, что масса этих частиц, летящих в ускорителе по кругу, не уменьшается, а наоборот, растёт с ростом скорости У в полном соответствии с формулой теории относительности (16.1), отличающейся от предлагаемой формулы (16.21) только знаком дроби вместо знака умножения между сомножителями.
Автор снимает шляпу перед внимательностью такого читателя, ибо он действительно немножко недоговорил в предыдущем разделе. Там преднамеренно велась речь только о системе, состоящей из двух тел с одинаковыми массами. При ускорении вращения системы они "худеют" одинаково. А вот если бы мы там вместо того, чтобы перейти к задаче с двумя одинаковыми массами, продолжали бы рассматривать задачу о вращении планеты вокруг Солнца, то пришли бы к конфузу. Действительно, тогда мы затруднялись бы сказать, к чему относится формула (16.21) - только ли к массе планеты или к массе всей Солнечной системы. Если предположить, что только к массе планеты (или другого тела, обращающегося вокруг намного более массивного тела), то эта формула сразу вступила бы в противоречие с тем экспериментальным фактом, что масса элементарной частицы при ускорении её в циклическом ускорителе не уменьшается, а возрастает.
Если же решить, что в соответствии с формулой (16.21) должна уменьшаться масса всей Солнечной системы, то это тоже будет явной ошибкой: почему это ускорение обращения вокруг Солнца-какой-то малой планеты, масса которой в сотни тысяч раз меньше солнечной, должно заставить Солнце быстро и ощутимо "похудеть"? Явная нелепость!
Увы, формула (16.21) справедлива только по отношению к симметричным системам типа позитрония, двойных звёзд или колеса. А к существенно несимметричным, жим как система звезда-планета или ускоритель с летящей в нём по кругу элемен тарной частицей, применима лишь формула (16.20), которая подсказывает, что масса-энергия системы должна уменьшиться на величину энергии связи, возникающей в этой системе.
Вы спросите, как перераспределяется энергия связи между неравными телами системы? Какие из них больше теряют в массе и почему? Ответа на этот вопрос у современной науки, по-видимому, нет. Автор только догадывается, что энергия связи между телами вращающейся системы перераспределяется пропорционально массам этих тел. Чем больше масса одного тела по сравнению с другим, тем больше (по абсолютной величине) массы-энергии теряет это тело. Так, когда образуется атом водорода из протона и электрона с выделением 14 эВ энергии излучения, то в результате появляющегося "дефекта массы" больше легчает протон, чем электрон. Хотя в процентном отношении оба они легчают, наверно, одинаково относительно массы каждого из них. Увы, теоретики этим вопросом не интересовались, прикрываясь принципом неопределённостей квантовой механики.
А доказательством правильности нашей догадки как раз и служит опыт эксплуатации циклических ускорителей. В них при ускорении частицы, мчащейся по круговой траектории, масса-энергия этой частицы не уменьшается, а возрастает почти точно в соответствии с формулой (16.1). Но при этом энергия связи такой частицы с ускорителем, в соответствии с теоремой вириала, должна возрастать быстрее, чем возрастает масса-энергия частицы. Мы не говорим "в два раза быстрее" потому, что при околосветовых скоростях полёта частиц в ускорителе работает уже не классическая, а релятивистски обобщённая теорема вириала, в уравнении (16.16) которой член под знаком радикала уже существенно меньше единицы. (Точнее, он настолько меньше единицы, что уже мало отличается от нуля.) При этом система ускоритель-частица должна излучать энергию, равную энергии связи частицы с ускорителем, за счёт которой обеспечивается удержание частицы на круговой траектории при всё возрастающих в процессе ускорения центробежных силах, стремящихся отбросить частицу к стенкам ускорительной камеры.
И такое излучение из циклических ускорителей действительно наблюдается - это всем известные циклотронное и синхротронное излучения. Их интенсивность пропорциональна квадрату тангенциальной скорости частицы 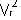[177], как это и должно быть в соответствии с нашей формулой (16.14).
Но, конечно же, теоретики объясняют синхротронное излучение отнюдь не теоремой вириала. Они полагают, что это излучение рождается лишь за счёт центростремительного ускорения заряженных частиц при искривлении их траекторий силами Лоренца, когда частицы движутся поперёк силовых линий магнитного поля ускорителя [ 20 ]. Излучение же, предсказываемое теоремой вириала, должно появляться только в результате увеличения кинетической энергии частицы при её ускорении. Это значит, что при движении ускоренных частиц в кольцевом накопителе, где они уже не ускоряются, не должно наблюдаться излучения, обусловленного теоремой вириала, хотя магнитное поле и там искривляет траектории этих частиц. Интересно, сумеют ли физики-экспериментаторы выделить такое излучение из обыкновенного синхротронного? А может (чем чёрт не шутит!) и само синхротронное излучение обусловлено только теоремой вириала, и его в кольцевых накопителях вообще не окажется?
Ведь в планетарной модели атома электрон летит по круговой орбите, не излучая. Отсутствие излучения из невозбуждённого атома противоречит сложившимся у физиков представлениям, согласно которым электрон при любом искривлении его траектории должен излучать электромагнитные волны. Потому физики при первой же возможности отказались от планетарной модели атома и перешли к представлению о размазанном "электронном облаке", окутывающем ядро атома со всех сторон одновременно. В такой модели атома уже нечему вращаться.
Но вот в середине XX века был синтезирован позитроний - система из электрона и позитрона, обращающихся вокруг их общего центра масс - пустого места. Тут без вращения уже никак не обойтись. А ведь позитроний тоже не излучает!
Теорема вириала подсказывает нам, что электрон не излучает в атоме и позитронии потому, что там его вращение не ускоряется, и его тангенциальная скорость остаётся неизменной по абсолютной величине.
Атом не должен излучать, даже если рассматривать его с точки зрения классической электродинамики, уверяет "нерелятивист" Н. К. Носков из Национального ядерного центра Казахстана. Он указывает, что в ныне почти забытых уравнениях классической электродинамики В. Вебера фигурирует не векторная, а скалярная величина расстояния между движущимися заряженными частицами. Это означает, что при обращении электрона по круговой равновесной орбите вокруг ядра атома, когда расстояние между ядром и электроном остается неизменным, электрон и не должен излучать!
Не будем вмешиваться в этот спор электрофизиков, а только добавим, что когда электрон в атоме находится на равновесной орбите, он уже имеет необходимую для поддержания такого равновесия энергию связи с ядром, и атом уже имеет дефект массы, соответствующий этой энергии связи. А в синхротроне, где электрон непрерывно ускоряется, необходимая энергия связи его с ускорителем должна непрерывно возрастать. Вот и происходит непрерывная генерация синхротронного излучения для образования необходимого "дефекта массы" в системе ускоритель-электрон.
Тут знатоки ускорительной техники язвительно подметят, что, во-первых, в синхротроне электрон тоже летит по равновесной круговой траектории, но тем не менее излучает. Во-вторых, скажут они, электрон там излучает не только в то время, когда он ускоряется электрическим полем в дуантах ускорителя, но и когда он летит по инерции (уже без ускорения) по круговой траектории между полюсами магнитов ускорителя, где нет ускоряющего поля. Последнее обстоятельство, скажут они, в пух и прах разбивает гипотезу о том, что причиной синхротронного излучения является увеличение скорости частиц.
Но оппоненты и тут будут неправы. Дело в том, что после получения ускоряющего импульса в дуанте электрон летит между полюсами магнита не по равновесной траектории, а как та планета, получившая избыток скорости, о которой мы рассказывали в предыдущем разделе, переходит на неравновесную эллиптическую траекторию. Чтобы вернуться на равновесную траекторию, электрон должен излучить лишнюю энергию. Ему, в отличие от планеты, это легко сделать - ведь он электрически заряжен и движется поперёк силовых линий магнитного поля ускорителя. Вот он и излучает электромагнитные волны. Излучает, уже находясь далеко за пределами дуанта.
Так и электроны в атомах часто под воздействием внешнего толчка переходят с равновесной на неравновесную орбиталь - атом возбуждается. Через какое-то время электрон в нём всё же возвращается на равновесную орбиталь, высветив квант излучения. Почти как в синхротроне. Спрашивается, кто высвечивает это излучение, электрон или атом? Физики давно согласились, что весь атом.
Так и в случае с ускорителем синхротронное излучение генерируют не сами электроны, а система электрон-ускоритель. И львиную долю энергии в это излучение вкладывает именно ускоритель. Потому-то масса электрона, ускоряемого в циклическом ускорителе, не уменьшается, а возрастает.
Возрастает она потому, что в массу превращается та кинетическая энергия, которую приобретает электрон при его ускорении. А излучается в виде синхротронного излучения энергия связи ускоряемого электрона с ускорителем. Притом в это излучение превращается почти исключительно масса-энергия ускорителя, а не ускоряемой частицы.
Увы, это не означает, что в излучение превращается часть железа ускорителя. Нет, синхротрон не является тем инструментом, который мог бы позволить нам непосредственно превращать массу вещества в излучение. В энергию излучения в нём переходит часть энергии электромагнитных полей ускорителя. Проще говоря,? синхротронное излучение уходит часть той электроэнергии, которую потребляет ускоритель от внешней сети.
Вы рассмеетесь: это ж надо было так долго рассуждать, чтобы прийти к столь азбучной истине! Не смейтесь. Ибо теперь Вы, будем надеяться, поняли: для убеждения в нашей правоте в том, что теорема вириала имеет отношение и к синхротронному излучению, достаточно просто измерить полную (интегральную) мощность синхротронного излучения ускорителя и сопоставить её с мощностью, приобретаемой ускоряемыми частицами. Согласно уравнению (16.16), при околосветовых скоростях электронов эти мощности будут почти равны друг другу. Интересно, ускорителыцики проводили такие сопоставления или их ещё только предстоит сделать?

Date: 2015-07-27; view: 508; Нарушение авторских прав