Линия без искажений и линия без потерь

Независимость от частоты Z и a и линейная зависимость b(w) — выполняются, если параметры линии R, L, C, G удовлетворяют условию

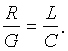
Рассмотрим преобразование общих выражений для Z и g при учете последнего условия:

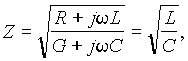
а для коэффициента распространения имеем:

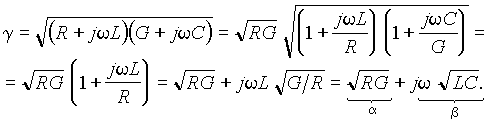
Линия, удовлетворяющая полученным соотношениям, называется неискажающей. Если на вход такой линии подается сигнал произвольной формы, то на выходе, нагруженном на сопротивление, равное волновому, появляется сигнал той же формы, уменьшенный в e ^{a l} раз и задержанный на время пробега вдоль линии t = l/v = l Ö LC. Волновое сопротивление неискажающей линии вещественно, а скорость распространения сигналов не зависит от частоты и равна v = w/b = 1/Ö LC.

Частным случаем неискажающей линии является линиябезпотерь, у которой R = 0 и G = 0. В этом случае, очевидно, Z = Ö L/C, g = j b, a = 0, b = wÖ LC. В такой линии амплитуды волн при распространении не уменьшаются.

закон полного тока

закон электромагнитной индукции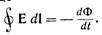

постулат Максвелла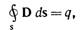

непрерывность линий вектора магнитной индукции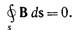

Теорема Гаусса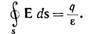

Закон полного тока в дифференциальной форме — первое уравнение Максвелла

Закон электромагнитной индукции в дифференциальной форме — второе уравнение Максвелла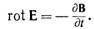

Теорема Гаусса в дифференциальной форме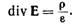

постулат Максвелла в дифференциальной форме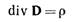

div B=0,

,

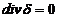Date: 2015-07-27; view: 486; Нарушение авторских прав