ЭЛЕКТРОДИНАМИЧЕСКАЯ СТОЙКОСТЬ ЭЛЕКТРИЧЕСКИХ АППАРАТОВ. РАСЧЕТ ЭЛЕКТРОДИНАМИЧЕСКИХ УСИЛИЙ

При прохождении электрического тока токоведущие части аппарата испытывают механические усилия.

Электродинамической стойкостью электрического аппарата называется способность выдерживать без повреждений и нарушений функционального состояния механические воздействия, создаваемые проходящим по нему электрическим током.

Для количественной оценки этого явления вводится понятие тока электродинамической стойкости. Наибольшее мгновенное значение амплитуды тока короткого замыкания называется ударным током короткого замыкания. Ток электродинамической стойкости электрического аппарата должен быть больше ударного тока короткого замыкания для данных условий работы.

Задача расчета электродинамических усилий решается по законам Био-Савара-Лапласса и Ампера, либо по энергетическим формулам.

По закону Ампера электродинамическое усилие, действующее на линейный проводник с током, находящийся в однородном магнитном поле, определяется из выражения

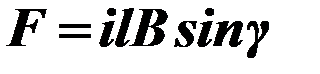, (63)

где 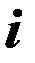– значение тока, А;

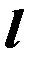– длина проводника, м;

B–магнитная индукция, Т;

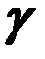– угол между направлением тока и вектором индукции.

В векторной форме закон Ампера

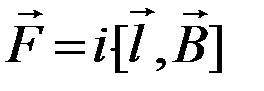. (64)

Проводник длиной 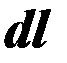с током 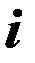создаст напряженность магнитного поля dH на расстоянии 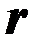от середины длины 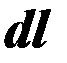– закон Био-Савара-Лапласса:

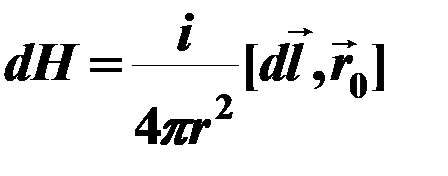, (65)

где 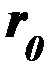– единичный вектор, направление которого совпадает с направлением луча, проведенного из середины проводника .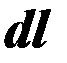

Элементарная индукция

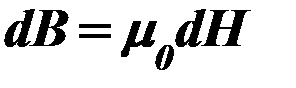. (66)

Если имеется два проводника с токам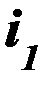и и 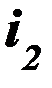, то усилие, действующее на один проводник со стороны другого, с учетом (63–65) определяется из соотношения

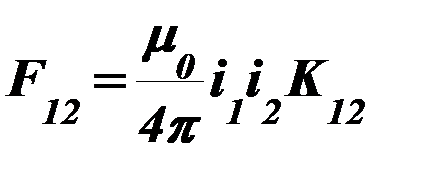, (67)

где 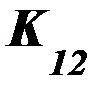- коэффициент контура электродинамических усилий, зависящий от геометрических размеров токо-ведущего контура.

Значения коэффициентов контура сведены в таблицу [табл. П.4].

Если необходимо учесть конкретные размеры проводников, то используют формулу

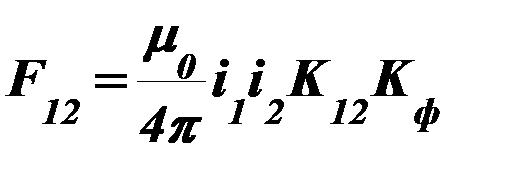, (68)

где 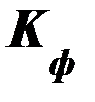- коэффициент формы поперечного сечения, некоторые значения которого приведены на рис. П.5.

В тех случаях, когда необходимо определить электродинамическое усилие для катушек или витков, в которых индуктивность L или взаимоиндуктивность М могут быть выражены как функции координаты, в направлении которой вычисляется сила взаимодействия, используются энергетические формулы.

Обобщенное усилие, действующее на проводник, при 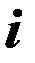=const

, (69)

где W– электрическая энергия, Дж;

g– обобщенная координата, м.

Так как в линейных системах

,

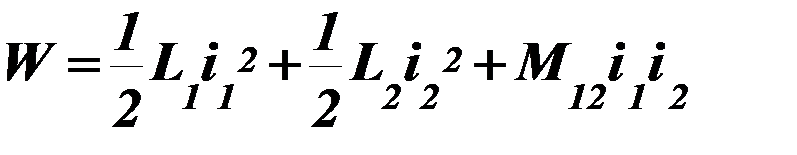то .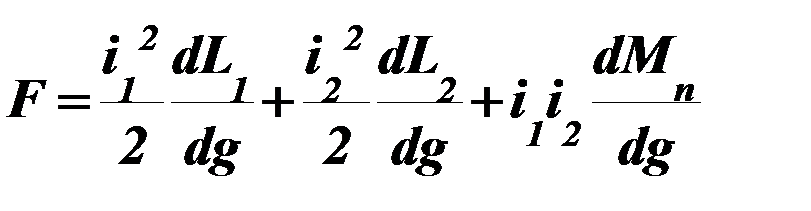

Электродинамическое усилиев проводниках при изменении поперечного сечения (усилие Двайта) определяется по формуле:

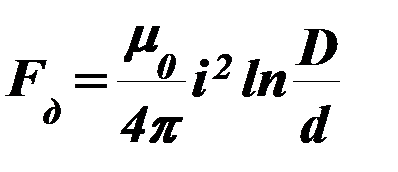, (70)

где D, d –соответственно диаметры большего и меньшего поперечного сечения.

Рассмотрим круговой виток радиуса Rc током i, выполненный из проводника радиуса r (рис.56).

При R>>r индуктивность L круглого витка определяется по формуле из таблицы (П.6)

Рис.56

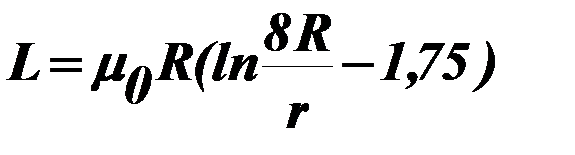. (71)

Тогда усилие, направленное на увеличение радиуса R и равномерно распределенное по окружности , равно:

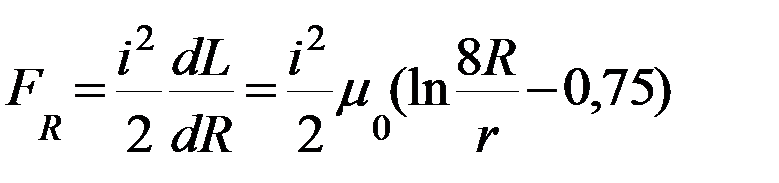.(72)

Кроме того, существует усилие, направленное на уменьшение радиуса r проводника с током и равномерно распределенное по окружности ,

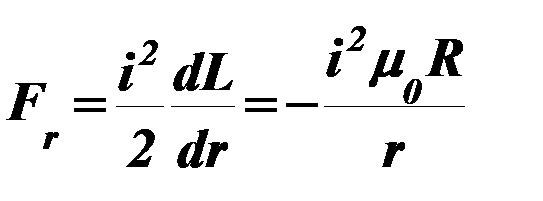. (73)

Если в токоведущих частях электрического аппарата проходит однофазный переменный ток

,

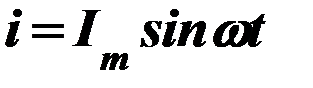то электродинамическое усилие определяется по тем же законам, что и на постоянном токе.

Например, электродинамическое усилие (э.д.у.), действующее на проводник с током, находящийся в магнитном поле другого проводника с тем же током, определяется из выражения

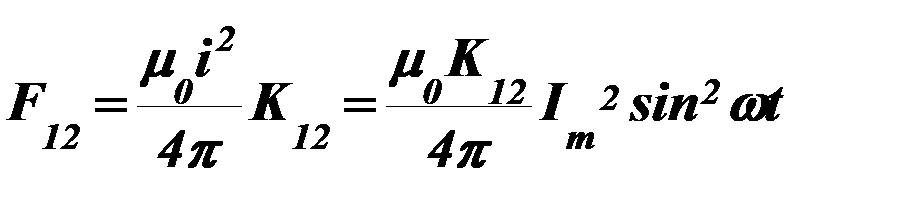. (74)

Последнее выражение можно преобразовать к виду

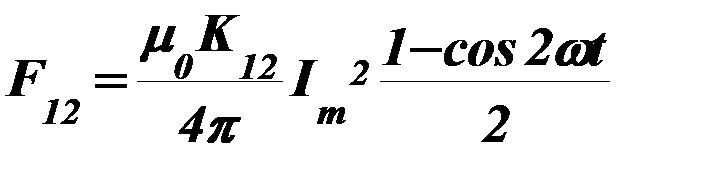, (75)

из которого видно, что электродинамическое усилие 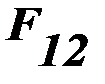изменяется с удвоенной частотой по сравнению с частотой тока и включает постоянную составляющую.

Из выражения (75) следует, что максимальное усилие

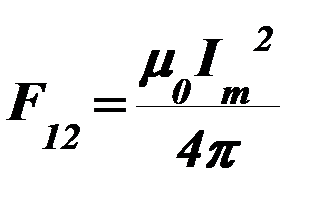. (76)

Ток короткого замыкания имеет зависимость

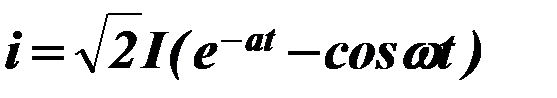, (77)

где I– действующее значение периодической состав-ляющей тока короткого замыкания;

– постоянная затухания, которая зависит от параметров источника и цепи.

Ударным током короткого замыкания называется максимальное значение мгновенного тока короткого замыкания. Из выражения (77) следует, что оно достигается при .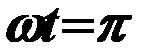

Если среднее значение =22 1/c, то при частоте тока f=50 Гц

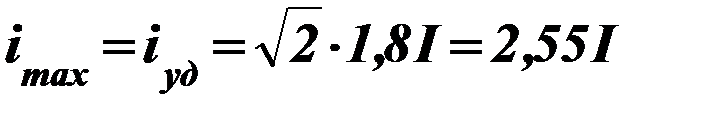. (78)

В трехфазных цепях токи в отдельных фазах определяются из выражений:

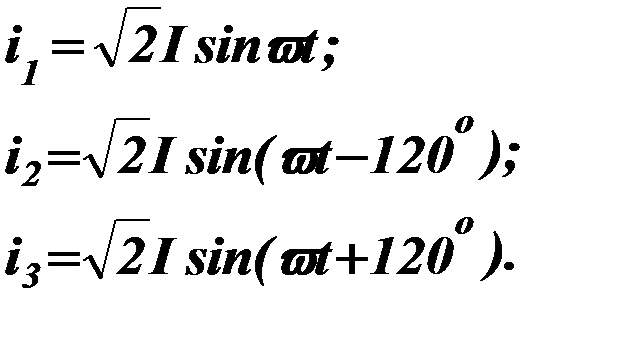
Усилия, действующие на проводник каждой фазы, определяются из выражения (67).

Так, на проводник первой фазы действует усилие

.

Если провода фаз расположены параллельно друг друга в одной плоскости, то векторы 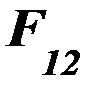и 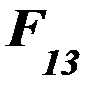складываются:

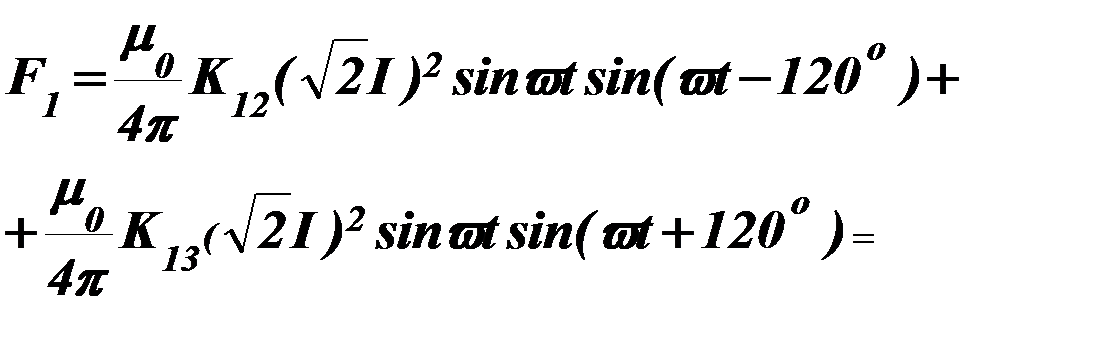
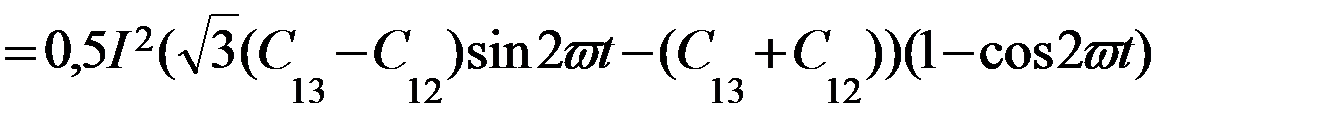,(79)

где .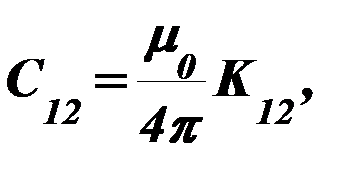

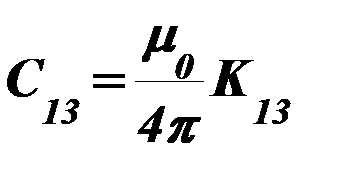Из выражения (79) следует, что F изменяется с удвоенной частотой

oт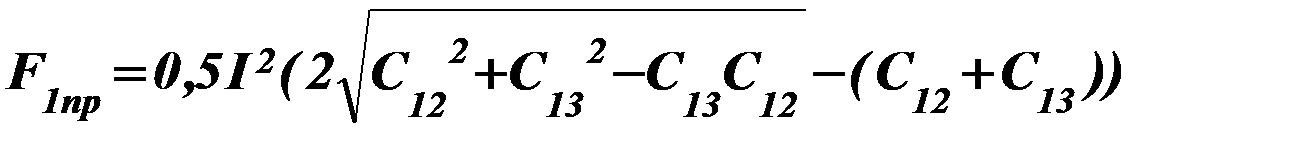

до .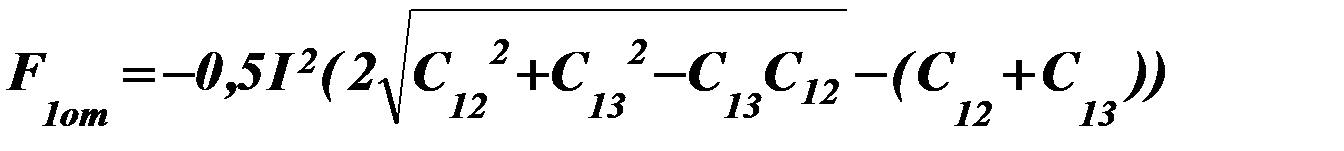

Усилие 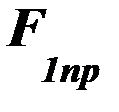называемое притягивающим, направлено на притяжение первой фазы к двум другим. Усилие , называемое отталкивающим, направлено на отталкивание первой фазы от второй и третьей.

Если провода расположены таким образом, что расстояние между первым и третьим в два раза больше, чем между первым и вторым (рис. 57), то

, ,

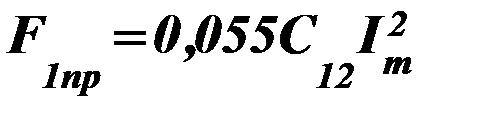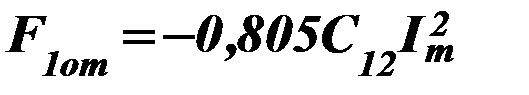
или 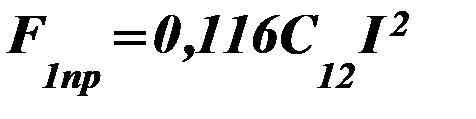, 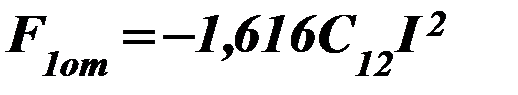. (80)

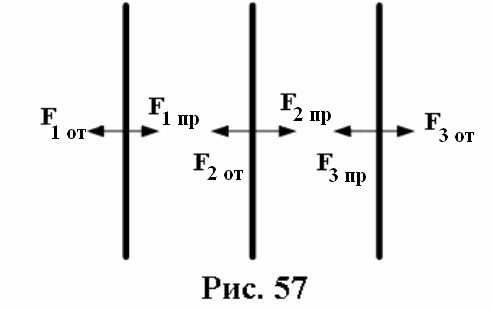
Усилия, действующие на проводник третьей фазы, как для первой фазы.

, .

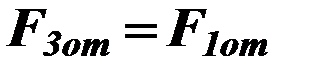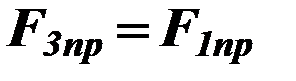Электродинамические усилия, действующие на средний провод (вторая фаза), будут изменяться с частотой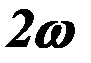

от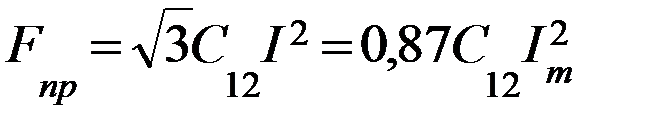

до .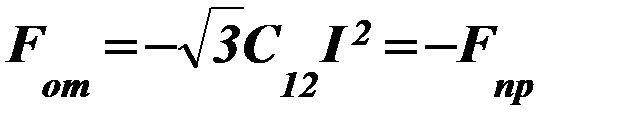

Date: 2015-07-27; view: 10960; Нарушение авторских прав