Понятие и классификация рядов динамики. Сопоставимость уровней и смыкание рядов динамики

Динамика – процесс развития движения соц.эк. явлений во времени. Для её отображения строят ряды динамики. Ряд динамики представл. Собой ряд расположенных в хронологической последовательности знач. Стат. показателей, характер. развитие явления Анализ рядов динамики позволяет выявить тенденции и закономерности соц.эк развития. Ряд динамики состоит из 2-ух элементов: 1)показатели времени (t) – либо определенные даты, либо отдельные периоды (годы, кварталы и тд.) 2)Уровни ряда (y) – они отображают количественную оценку развития во времени изучаемого явления. Виды рядов динамики: 1. По времени отражаемому в динамич. Рядах они делятся на: - моментальные отображают состояние изучаемых явлений на опр даты (моменты времени) С помощью моментных рядов изучают: численность населения, стоимость осн средств, товар запасы. Уровни мом. Рядов динамики суммировать не имеет смысла, т.к. мож. Возникнуть повторный счет – интервальные – отображают итоги развития изучаемого явления за отдельные периоды (интервалы времени): ряды динамики произ-ва прод-ции, инвестиций, затраченных средств. Уровни интервального ряда динамики абсолют. Величин мож суммировать, т.к. их можно рассматривать как итог за более длительный период времени. 2. В зависимости от способа выражения уровней ряда динамики различают ряды: - абсолютных величин, - относительных, - средних величин. 3. В зависимости от расстояния м/у уровнями различ. ряды динамики с равностоящими и не равностоящими уровнями во времени. Основ условием для получения правильных выводов при анализе ряда динамики явл-ся сопоставимость его уровней. Условия сопоставимости уров. Ряда динамики. 1)Долж. Быть обеспечена одинаковая полнота охвата различных частей явления. Уровни динамического ряда за отдельные периоды времени долж харка-вать размер явления по одному и тому же кругу, входящий в его состав частей. 2)При определении сравниваемых уровней ряда динамики необх. Использовать единую методологию их расчета. 3)Равенство периодов, за к-рые приводятся данные. 4)Необходимо использовать одинаковые единицы измерения. При харак-ки стоимостных показателей во времени долж. б. устранено влияние изменение цен необх. оценка изучаемого показ-ля в ценах одного периода (в сопоставимых ценах) 5)Исходя из цели исследов-ия данные по тер-риям, границы которые изменились долж. б. пересчитаны в старых пределах. Для приведения уровней ряда дин-ки к сопоставимому виду использ. Прием, который наз-ся Смыкание рядов динамики. Смыкание- объединение в один ряд двух или нескольких рядов динам., уровни которых исчислены по разной методике или разными территориальными границами. Чтобы произвести смыкание рядов необх, чтобы для одного из периодов (переходного) имелись данные, рассчитанные по разной методике или в разных границах.

21. Показатели интенсивности изменения уровня ряда динамики. Цепной и базисный способы расчёта.

Для качественной оценки динамики, изучаемых явлений применяется ряд стат. показателей получаемых в результате сравнения уровней м/у собой. При этом сравниваемый уров. Наз-ся отчетный, а уров., с которым происх. Сравнение базисным. К основ. показателям динамики относятся абсолют. Прирост, темп роста, темп прироста, абсолют. Значение одного % прироста. В зависимости от применяемого способа сопоставления показатели динамики мог. вычисляться с постоянной и переменной базой сравнения y_1←y_2←y_3←y_4←y₅ Абсолютный прирост характ. размер увеличения или уменьшения уровня ряда динамики за определенный период времени и определ-ся как разность м/у 2-мя уровнями ряда. ∆y_ц = y_i – y _i -_{1 ∆}y_б = y_i – y ₀ м/у цепным и базисными абсолютными приростами сущ-ет взаимосвязь: сумма ценных абсол-ых приростов равна базисному абсол-му приросту последнего периода ряда динамики. ∑∆y_ц = ∆ y_бп Темп роста характеризует интенсивность изменения уравнения ряда и показывает во сколько раз уров. текущего периода больше или меньше уровня предыдущего (базисного) периода или сколько % он составляет по отношению к предыдущему периоду Трц = y_i/y_i-1 * 100% Трб = y_i/y₀ * 100% м/у цепными и базис темпами роста имеется взаимосвязь: произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста последнего периода ряда динамики. П Крц = Крб Темп прироста показывает на сколько % - ов уров. данного периода больше или меньше уровня принятого за базу сравнения: Он мож б рассчитан 2 способами: а) как отношение абсол.-го прироста к уровню, принятому за базу сравнения Тпрц = ∆ y_i / y_i-1 * 100% Тпрб = ∆ y_i / y₀ * 100% б) как разность м/у темпом роста и 100%-ми Тпр = Тр – 100% Абсолютное значение 1% присрота показывает какая абсло-ая величина содержится в относ-ном показателе – одном % прироста. Это отношение абсло-ого прироста к темпу прироста, выраженному в %-ах. Данный показатель рассчитывается по цепным данным А_%=∆ y_i / Тпр % = ∆ y_i / (∆ y_i/ y_i-1)*100 = y_i-1 / 100 Для получения обобщающих показателей динамики соц.эк. явлений определяют средние величины: ср уровень ряда, сред абсол-ый прирост, след темп роста, сред темп прироста. Средний уровень ряда динамики дает общую характ-ку уровня явлен. За весь период. Методы его расчета зависят от вида ряда динамики. а)
для моментных рядов для ровно стоящими расчит сред. уров. ряда осущ-ся по форм. средней хронологич-кой. y` = (½ y<sub>1</sub> + y<sub>2</sub> + y<sub>3</sub> + ….½y<sub>n</sub>)/n-1 n – число уровней ряда. б)для моментных рядов с не равностоящими уров-ми предварительно находятся значения уровней в серединах интервалов y`₁ = y₁ + y₂ /2; y₂ = y₂ + y₃/2,……..,y`<sub>n</sub> = y<sub>n-1</sub> + y<sub>n</sub>/2 Затем определяется общий сред уров. ряда по формуле средней арифм-ой взвешенной: y` = ∑y`<sub>i</sub>* t<sub>i</sub> / ∑t<sub>i</sub> y`_I – сред уровни в интервалах м/у датами, ti – длительность интервала времени м/у уровнями. в) Для интервальных рядов с равностоящими уровн-ми во времени, сред уров расситыв-ся по формуле средней арифм-кой простой y` = ∑ y_i /n Средний абсолютгый прирост показывает на сколько в среднем за единицу времени увеличивается (уменьшается) уровень ряда. ∆ y_i = ∑ y_iц / n-1 или ∆ y_i = y_n – y₁/n-1

y1 – начальный уровень ряда динамики yn – конечный уровень ряда динамики. Средний темп роста показывает во сколько раз в среднем за единицу времени изменился уровень ряда динамик. Он опред-ся по форм. средней геометрической из цепных коэф-тов роста. Т`р = ^{n – 1} √К^цр₁ * К^цр₂ *……*К^цр_{n – 1} = ^{n – 1} √ ПКр^ц = ^{n -1} √Крб = ^{n – 1} √ y_n/y₁ * x 100%

Средний темп прироста показ-ет на сколько % в среднем за единицу времени увеличился (уменьшился) уровень ряда Т`пр = Т` - 100%.

22. Средние показатели ряда динамики, их расчёт.

Каждый ряд динамики можно рассматривать как некую совокупность n меняющихся во времени показателей, которые можно обобщать в виде средних величин. Такие обобщенные (средние) показатели особенно необходимы при сравнении изменений того или иного показателя в разные периоды, в разных странах и т.д.

Обобщенной характеристикой ряда динамики может служить прежде всего средний уровень ряда. Способ расчета среднего уровня зависит от того, моментный ряд или интервальный (периодный).

В случае интервального ряда его средний уровень определяется по формуле простой средней арифметической величины из уровней ряда, т.е.

=
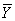Если имеется моментный ряд, содержащий n уровней (y1, y2, …, yn) с равными промежутками между датами (моментами времени), то такой ряд легко преобразовать в ряд средних величин. При этом показатель (уровень) на начало каждого периода одновременно является показателем на конец предыдущего периода. Тогда средняя величина показателя для каждого периода (промежутка между датами) может быть рассчитана как полусумма значений у на начало и конец периода, т.е. как . Количество таких средних будет . Как указывалось ранее, для рядов средних величин средний уровень рассчитывается по средней арифметической. Следовательно, можно записать
.
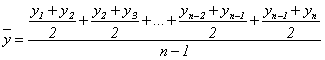После преобразования числителя получаем
,

где Y1 и Yn — первый и последний уровни ряда; Yi — промежуточные уровни.

Эта средняя 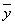известна в статистике как средняя хронологическая для моментных рядов. Такое название она получила от слова «cronos» (время, лат.), так как рассчитывается из меняющихся во времени показателей.

В случае неравных промежутков между датами среднюю хронологическую для моментного ряда можно рассчитать как среднюю арифметическую из средних значений уровней на каждую пару моментов, взвешенных по величине расстояний (отрезков времени) между датами, т.е.
.
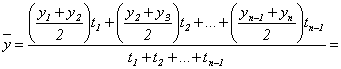
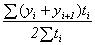В данном случае предполагается, что в промежутках между датами уровни принмали разные значения, и мы из двух известных (yi и yi+1) определяем средние, из которых затем уже рассчитываем общую среднюю для всего анализируемого периода.
Если же предполагается, что каждое значение yi остается неизменным до следующего (i+ 1 )- го момента, т.е. известна точная дата изменения уровней, то расчет можно осуществлять по формуле средней арифметической взвешенной:
,

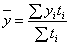где 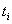– время, в течение которого уровень 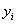оставался неизменным.

Кроме среднего уровня в рядах динамики рассчитываются и другие средние показатели – среднее изменение уровней ряда (базисным и цепным способами), средний темп изменения.

Базисное среднее абсолютное изменение представляет собой частное от деления последнего базисного абсолютного изменения на количество изменений. То есть

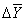Б =

Цепное среднее абсолютное изменение уровней ряда представляет собой частное от деления суммы всех цепных абсолютных изменений на количество изменений, то есть

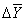Ц =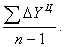

По знаку средних абсолютных изменений также судят о характере изменения явления в среднем: рост, спад или стабильность.

Из правила контроля базисных и цепных абсолютных изменений следует, что базисное и цепное среднее изменение должны быть равными.

Наряду со средними абсолютным изменением рассчитывается и среднее относительное тоже базисным и цепным способами.

Базисное среднее относительное изменение определяется по формуле

Б= =

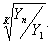
Цепное среднее относительное изменение определяется по формуле

Ц=

Естественно, базисное и цепное среднее относительное изменения должны быть одинаковыми и сравнением их с критериальным значением 1 делается вывод о характере изменения явления в среднем: рост, спад или стабильность.
Вычитанием 1 из базисного или цепного среднего относительного изменения образуется соответствующий среднийтемп изменения, по знаку которого также можно судить о характере изменения изучаемого явления, отраженного данным рядом динамики.

Date: 2015-07-27; view: 1094; Нарушение авторских прав