Структурные средние величины

В отличие от степенных средних, которые в значительной степени являются абстрактной характеристикой совокупности, мода и медиана выступают как конкретные величины, совпадающие с вполне определенными вариантами совокупности. Это делает их незаменимыми при решении ряда практических задач.

Мода - значение признака, наиболее часто встречающееся в исследуемой совокупности (т.е. варианта с наибольшей частотой).

Медиана - значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части.

Ранжированный ряд – это ряд, расположенный в порядке возрастания или убывания значения признака.

Определение моды и медианы по не сгруппированнным данным осуществляется несложно.

Например, предположим, что одинаковый товар в различных магазинах города продается по различным ценам, рублей:

93, 75, 84, 93, 71, 75, 89, 82, 93, 89,82, 76

Чаще всего встречается цена 93 руб. Следовательно, она является модальной.

Для определения медианы необходимо провести ранжирование (упорядочивание):

71, 75, 75, 76, 82, 82, 84, 89,89, 93,93, 93

Центральная цифра в данном ряду и будет медианой. Если ранжированный ряд, как в нашем случае, включает чётное число единиц, то медиана определяется как средняя из двух центральных значений - 82 и 84 - средняя – 83- медиана.

Что касается сгруппированных данных, то для дискретных вариационных рядов модой будет значение варианта с наибольшей частотой. Вычисление медианы в дискретных рядах распределения имеет специфику.

Мода выбирается по максимальному значению частоты.

Для нахождения медианы (Me) определяют медианный интервал, который характеризуется тем, что его накопленная частота равна или превышает половину суммы всех частот ряда (.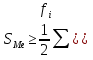

В интервальном ряду значения Mo и Me вычисляются более сложным путем.

Мода определяется следующим образом:

1. По максимальному значению частоты определяется интервал, в котором находится значение моды. Он называется модальным.

2. Внутри модального интервала значение моды вычисляется по формуле:

,

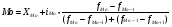где Х_Mo – нижняя граница модального интервала;

iMo – величина модального интервала;

f_Mo – частота модального интервала;

f_Mo-1 – частота интервала, предшествующего модальному;

f_Mo+1 – частота интервала, следующего за модальным.

Для расчета медианы в интервальных рядах используется следующий подход:

1. По накопленным частотам находится медианный интервал, который характеризуется тем, что его накопленная частота равна или превышает половину суммы всех частот ряда (.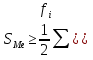

2. Внутри медианного интервала значение Me определяется по формуле:

,

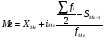где X_Me – нижняя граница медианного интервала;

iMe – величина медианного интервала;

∑ fi – сумма частот;

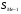– сумма накопленных частот, предшествующих медианному интервалу;

f_Me – частота медианного интервала.

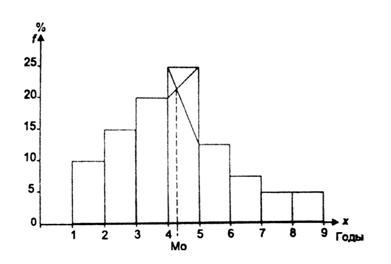
Моду и медиану в интервальном ряду можно определить графически. Мода определяется по гистограмме распределения. Для этого выбирается самый высокий прямоугольник, который является в данном случае модальным. Затем правую вершину модального прямоугольника соединяем с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника - с левым верхним углом последующего прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось абсцисс. Абсцисса точки пересечения этих прямых и будет модой распределения.

15. Средняя арифметическая простая и взвешенная. Методика расчёта и условия применения средней арифметической.

Под средней арифметической понимается та­кое значение признака, которое имела бы каждая единица совокупности, если бы общий итог всех значений признака был распределен равномерно между всеми единицами совокупности. В общем случае ее вычисление сводится к суммированию всех значений варьирующегося признака и деле­нию полученной суммы на общее количество еди­ниц совокупности. Следует применить формулу простой средней арифметической:

Наряду с простой средней арифметической изу­чают среднюю арифметическую взвешенную, ко­торую используют, когда значения вариантов встречаются по несколько раз. Формула средней арифметической взвешенной имеет вид:

где х_i — варианты осредняемого признака;

f_i — частота, которая показывает, сколько раз встречается i-oe значение в совокупности.

Средняя арифметическая применяется в тех случаях, когда общий объем варьирующегося при­знака для всей совокупности образуется как сум­ма значений признаков у отдельных ее единиц.

Часто при проведении статистических исследо­ваний приходится вычислять средние величины по данным вариационных рядов. Если ряд является дискретным, то для вычисления средней нужно значения вариантов умножить на соответствую­щие частоты и сумму этих произведений разде­лить на сумму частот.

Для интервального вариа­ционного ряда для каждой группы находится среднее значение интервала как полусуммы его верхней и нижней границ. Эти средние значения интервалов и будут новыми значениями вариан­тов, подлежащих усреднению.

Для моментного ряда с равными интервалами между датами (на­пример, когда известны уровни на начало каждого месяца или квартала, года) расчет среднего уров­ня ряда производится по формуле средней хронологической (модифицированная средняя арифме­тическая):

Определение средней арифметической в ряде случаев сопряжено с большими затратами време­ни и труда. Однако процедуру расчета средней можно упростить, если воспользоваться некото­рыми ее свойствами:

1) средняя постоянной величины равна ей самой:

А=А

2) произведение средней на сумму частот равно сумме произведений вариантов на частоты;

3) изменение каждого варианта на одну и ту же величину изменяет среднюю на ту же величину;

4) изменение каждого варианта в одно и то же чис­ло раз изменяет среднюю во столько же раз;

5) изменение каждого из весов в одно и то же количество раз не изменяет величины средней;

6) алгебраическая сумма отклонений всех ва­риантов от средней равна 0;

7) средняя суммы равна сумме средник.

1. Средняя занимает серединное положение в вариационном ряду. В строго симметричном ряду: М = М₀=М_е.

2. Средняя является обобщающей величиной и за средней не видны случайные колебания, различия в индивидуальных данных, она вскрывает то типичное, что характерно для всей совокуп­ности. К средней обращаются всякий раз, когда надо исклю­чить случайное влияние от­дельных факторов, выявить об­щие черты, существующие за­кономерности, получить полное и глубокое представление о наиболее общих и характерных особенностях всей группы.

3. Сумма отклоне­ний всех вариант от средней равна нулю: S (V-M)= 0. Это происходит потому, что средняя величина превышает размеры одних вариант и мень­ше размеров других вариант.

Иначе говоря, истинное отклонение вариант от истинной средней (d = v-М) может быть положительной и отрицательной величи­ной, поэтому сумма S всех "+"d и "—"d равна нулю.

Данное свойство средней используется при проверке правильности расчетов М. Если сумма отклонений вариант от средней равна нулю, то можно сделать вывод, что средняя вычислена правильно. На этом свойстве основан способ моментов для определения М. Ведь если условная средняя А будет равна истинной М, то сумма отклонений вариант от условной средней будет равна нулю.

Роль средних величин в биологии чрезвычайно велика. С одной стороны их используют для характеристики явлений в целом, с другой - они необходимы для оценки отдельных величин. При сравнении отдельных величин со средними получают ценные харак­теристики для каждой из них. Использование средних величин требует строгого соблюдения принципа однородности совокупности. Нарушение этого принципа искажает представление о реальных процессах.

Вычисление средних из неоднородной в социально-экономическом отношении совокупности делает их фик­тивными, искаженными. Следовательно, для того чтобы правильно использовать средние величины, надо быть уверенным в том, что они характеризуют однородные статистические совокупности.

16. Средняя гармоническая. Методика расчёта и условия применения средней гармонической.

Средняя гармоническая применяется в тех случаях, когда известны варианты осередняемого признака (x_i) и показатели, представляющие произведение вариантов на частоты или веса средней арифметич.

Это произведение x*f=F и служит в качестве весов или частот средней гармонической.

Средняя гармоническая может быть простой и взвешанной.

а) средняя гармоническая простая

x_i - варианты осередняемого признака

n - число вариантов осередняемого признака

Средняя гармоническая простая применятся в тех случаях, когда веса всех вариантов равны. В тех случаях, когда веса не равны, применяется средняя гармоническая взвешанная.

б) средняя гармоническая взвешанная

Средняя гармоническая - это средняя из обратных величин, поэтому ее применяют для расчета средней трудоемксти, которая является обратной величиной производительности труда (выработки).

На практике чаще всего применяются средняя арифметическая и средняя гармоническая. Чтобы правильно выбрать формулу средней, необходимо руководствоваться следующими правилами:

1. Средняя гармоническая применяется для расчета в тех случаях, когда показатеь, величина которого не известна находится в знаменателе исходного отношения (это экономическое содержание расчитываемое показателем)

ЗП=ФондЗП/ЧР

2. Если в искомом отношении не известен числитель, то для расчета применяют среднюю арифметическую взвешенную.