
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Понятие о рядах распределения
|
|
Статистический ряд распределения — упорядоченное распределение единиц совокупности на группы по определенному варьирующему признаку.
Ряды распределения представляют собой группировки особого вида, при которых по каждому признаку, группе признаков или классу признаков известны численность единиц в группе л ибо удельный вес этой численности в общем итоге. В зависимости от признака, положенного в основу ряда распределения, различают атрибутивные и вариационные ряды распределения.
Атрибутивными называют ряды распределения, построенные по качественным признакам. Ряды распределения принято оформлять в виде таблиц. Атрибутивные ряды распределения характеризуют состав совокупности по тем или иным существенным признакам. Данные, взятые за несколько периодов, позволяют исследовать изменение структуры явления или процесса.
Вариационными называют ряды распределения, построенные по количественному признаку. Вариационный ряд распределения может быть построен по непрерывно варьирующему признаку (когда признак может принимать любые значения в рамках какого-либо интервала) и по дискретно варьирующему признаку (когда признак принимает строго определенные целочисленные значения). Построение непрерывного (интервального) вариационного ряда основано на принципах статистической группировки.
Любой вариационный ряд состоит из элементов: вариантов и частот. Вариантами считаются отдельные значения признака, которые он принимает в вариационном ряду, т.е. конкретны значения варьирующего признака. Варианты могут выражаться числами положительными и отрицательными, абсолютными и относительными. Частоты — это численности отдельных вариантов или каждой группы вариационного ряда, т.е. это числа, показывающие, как часто встречаются те или иные варианты в ряду распределения. Обозначаются они fi Сумма всех частот определяет численность всей совокупности, ее объем:
Численности групп, выраженные в процентных долях единицы, называются частостями и обозначаются wi Сумма частостей равна 1, если они выражены в долях единицы, и 100 %, если они выражены в процентах.
В непрерывном вариационном ряду с равными интервалами частоты показывают степень заполнения интервала единицами совокупности. При неравных интервалах частоты не характеризуют степень их заполнения. В этом случае рассчитывается плотность распределения. Этот показатель определяется числом единиц совокупности, приходящимся в среднем на одну единицу ширины интервала. Абсолютная плотность распределения определяется отношением частоты на ширину интервала, относительная плотность распределения — отношением частости к ширине интервала.
Статистическая таблица как способ изложения сводных статистических данных.
Результаты сводки и группировки представляют в статистической таблице, которая явл. наиболее рациональной и наглядной формы изображения статистического материала. Стат называется таблица, которая содержит сводную числовую характеристику исследуемой совокупности по одному или нескольким сущ. ризнакам взаимосвязанным логикой эк. анализа. Внешне таблица представляет собой пересечение граф и строк.
| Название таблицы | ||||
| сказ | Заголовки граф. | |||
| подл | ||||
| А | 1 | 2 | 3 | 4 |
| наим. Ст. | ||||
| итог. Ст. | итог. Гр |
Ста. таблица содержит три вида заголовка: общий (отражает содержание таблице к какому месту и времени она относиться) верхние (характ. Содержание граф) и боковые (заголовки строк) Основными элементами стат. табл. Явл.: подлежащие и сказуемое. Подлежащие – это перечень единиц совокупности или группы т.е. объект изучения. Сказуемое- это те показатели с помощью которых характ. Подлеж. Табл. Обычно подл. располагается слева в виде названий строк, а сказуемое сверху в виде названий граф. В зависимости от строения подлеж стат табл делятся на простые, групповые и комбинационные. Простой называется таблица в подлеж которой нет группировок. Простые таблицы бывают а)перечневые – это таблицы подлежащие которых содержат перечень едениц изучаемого объекта б) территориальные – подлежащие которых содержат перечень территорий стран, городов и тд. в) хронологические – подлежащие которых приводятся периоды времени и даты. Групповыми называются таблицы подлеж которых содержат группировку единиц совокупности по двум и более признакам. По структурному строению различают стат таблицы с простой и сложной его разработкой. При простой разработке сказуемого – показатель определяющий её не подразделятся на подгруппы. Сложная разработка сказуемого предполагает деление признака, формирование его на подгруппы. Основные правила построения таблиц: 1)Таблица должна иметь подробное название, где указывается объект наблюдения, его территориальные и временные границы. 2)Графы и строки должны содержать единицы измерения если они общие для всех показателей то указывается в заголовке таблицы после названия, если разные, то каждой колонке или строке. 3)Округление чисел в пределах одной и той же строки следует производить с одинаковой степенью точности в групповых и комбинационных таблицах необходимо давать итоговые графы и строки. При оформлении таблиц применяются следующие условные обозначения: - (когда явление отсутствует) x – когда явление не имеет смыслового содержания, ……… (нет сведения) 0,0; 0,00 – (для отображения очень малых чисел)
11. Статистические графики: понятие, элементы, классификация.
Статистический график — это чертеж, на котором статистические совокупности, характеризуемые определенными показателями, описываются с помощью условных геометрических образов или знаков.
Значение графического метода в анализе и обобщении данных велико. Графическое изображение, прежде всего, позволяет осуществить контроль достоверности статистических показателей, так как представленные на графике, они делают более очевидными имеющиеся неточности, связанные либо с наличием ошибок наблюдения, либо с сущностью изучаемого явления. Графики также широко используются для изучения структуры явлений, их изменения во времени и размещения в пространстве. В них более выразительно проявляются сравниваемые характеристики и отчетливо видны основные тенденции развития и взаимосвязи, присущие изучаемому явлению или процессу.
При построении графического изображения должен быть соблюден ряд требований. Прежде всего, графики должны быть достаточно наглядными, так как весь смысл графического изображения как метода анализа в том и состоит, чтобы наглядно изобразить статистические показатели. Кроме того, график должен быть выразительным, доходчивым и понятным. Чтобы все эти требования выполнялись, каждый график должен включать ряд основных элементов: графический образ; поле графика; пространственные ориентиры; масштабные ориентиры; экспликацию графика.
Рассмотрим подробнее каждый из указанных элементов.
Графический образ (основа графика) — это геометрические знаки, то есть совокупность точек, линий, фигур, с помощью которых изображаются статистические показатели. Важно правильно выбрать графический образ, который должен соответствовать цели графика и способствовать наибольшей выразительности изображаемых статистических данных.
Поле графика — это часть плоскости, где расположены графические образы. Поле графика имеет определенные размеры, которые зависят от назначения графика.
Пространственные ориентиры графика задаются в виде системы координатных сеток. Система координат необходима для размещения геометрических знаков в поле графика. Наиболее распространенной является система прямоугольных координат. Для построения статистических графиков используется обычно только первый и изредка первый и четвертый квадранты.
В практике графического изображения применяются также полярные координаты. Они необходимы для наглядного изображения циклического движения во времени. В полярной системе координат (рис. 4.1) один из лучей, обычно правый горизонтальный, принимается за ось координат, относительно которой определяется угол луча. Второй координатой считается ее расстояние от центра сетки, называемое радиусом. На статистических картах пространственные ориентиры задаются контурной сеткой (контуры рек, береговая линия морей и океанов, границы государств) и определяют те территории, к которым относятся статистические величины.
Масштабные ориентиры статистического графика определяются масштабом и системой масштабных шкал. Масштаб статистического графика — это мера перевода числовой величины в графическую. Масштабной шкалой называется линия, отдельные точки которой могут быть прочитаны как определенные числа. Шкала имеет большое значение в графике. В ней различают три элемента: линию (или носитель шкалы), определенное число помеченных черточками точек, которые расположены на носителе шкалы в определенном порядке, цифровое обозначение чисел, соответствующих отдельным помеченным точкам. Как правило, цифровым обозначением снабжаются не все помеченные точки, а лишь некоторые из них, расположенные в определенном порядке. По правилам числовое значение необходимо помещать строго против соответствующих точек, а не между ними (рис. 4.2).
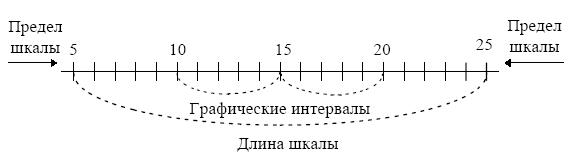
Рис.4.2. Масштабная сетка
Носитель шкалы может представлять собой как прямую, так и кривую линию. В соответствии с этим различают шкалы прямолинейные (например миллиметровая линейка) и криволинейные — дуговые и круговые (циферблат часов).
Графические и числовые интервалы могут быть равными и неравными. Если на всем протяжении шкалы равным графическим интервалам соответствуют равные числовые, такая шкала называется равномерной. Если же равным числовым интервалам соответствуют неравные графические, и наоборот, — шкала называется неравномерной.

Рис. 4.3. Масштабы
Масштабом равномерной шкалы называется длина отрезка (графический интервал), принятого за единицу и измеренного в каких-либо мерах. Чем меньше масштаб (рис. 4.3), тем гуще располагаются на шкале точки, имеющие одно и то же значение. Построить шкалу — это на заданном носителе шкалы разместить точки и обозначить их соответствующими числами согласно условиям задачи. Из неравномерных наибольшее распространение имеет логарифмическая шкала. Методика ее построения несколько иная, так как на этой шкале отрезки пропорциональны не изображаемым величинам, а их логарифмам. Так при основании 10 lg1 = 0; lg10 = 1; lg100 = 2 и т.д. Для этих величин логарифмическая шкала может быть представлена так, как это сделано на рис. 4.4.
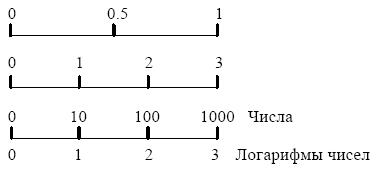
Рис.4.4. Шкалы
Последний элемент графика — экспликация. Каждый график должен иметь словесное описание его содержания. Оно включает в себя название графика, которое должно в краткой форме передавать его содержание, подписи вдоль масштабных шкал и пояснения к отдельным частям графика.
I. Виды статистических графиков по поставленным задачам:
1. Диаграммы сравнения.
2. Диаграммы динамики.
3. Диаграммы контроля выполнения плана.
4. Диаграммы структуры.
5. Графики вариационных рядов.
6. Графики зависимости варьирующих признаков.
7. Статистические карты.
II. Виды статистических графиков по форме графического образа:
1. Линейные графики – статистические кривые.
2. Плоскостные графики:
- столбиковые;
- полосовые (ленточные);
- секторные;
- круговые;
- квадратные;
- прямоугольные;
- фигурные;
- точечные;
- фоновые.
3. Объёмные графики – поверхностные распределения (пирамиды, параллелепипеды, сегментные графики и т. п.).
Date: 2015-07-27; view: 1275; Нарушение авторских прав