Дискретизация аналоговых сигналов. Ряд Котельникова

Всякое непрерывное сообщение s(t), занимающее конечный интервал времени Т_с, может быть передано с достаточной точностью конечным числом N отсчетов (выборок) s(nT), т.е. последовательностью коротких импульсов, разделенных паузой.

Дискретизация сообщений по времени – процедура, состоящая в замене несчетного множества мгновенных значений сигнала их счетным (дискретным) множеством, которое содержит информацию о значениях непрерывного сигнала в определенные моменты времени.

При дискретном способе передачи непрерывного сообщения можно сократить время, в течение которого канал связи занят передачей этого сообщения, с Т_с до 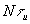, где 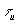- длительность импульса, применяемого для передачи выборки; можно осуществить одновременную передачу по каналу связи нескольких сообщений (временное уплотнение сигналов).

Наиболее простым является способ дискретизации, основанный на теореме В.А. Котельникова, сформулированной для сигналов с ограниченным спектром (теорема отсчетов):

если наивысшая частота в спектре функции s(t) меньше, чем F_m, то функция s(t) полностью определяется последовательностью своих значений в моменты, отстоящие друг от друга не более, чем на 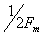секунд и может быть представлена рядом:

.

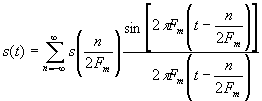(1)

Здесь величина 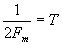обозначает интервал между отсчетами на оси времени, а

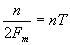- время выборки, 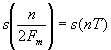- значение сигнала в момент отсчета.

Ряд (1) называется рядом Котельникова, а выборки (отсчеты) сигнала { s(nT) } иногда называют временным спектром сигнала.

Функция

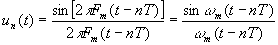
обладает следующими свойствами:

а) в точке t=nT функция равна 1, т.к. в этой точке аргумент функции 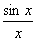равен 0, а значение ее равно 1;

б) в точках t=kT, 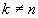функция 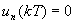, т.к. аргумент синуса в этих точках равен 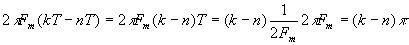, а сам синус равен нулю;

в) спектральная плотность функции u_n(nT) равномерна в полосе частот 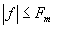и равна 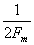. Этот вывод сделан на основе теоремы взаимности частоты и времени пары преобразований Фурье. ФЧХ спектральной плотности линейна и равна 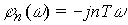(в соответствии с теоремой о сдвиге сигнала). Таким образом,

.

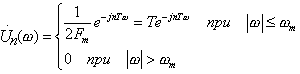Временное и частотное представления функции u_n(t) даны на рис.3.

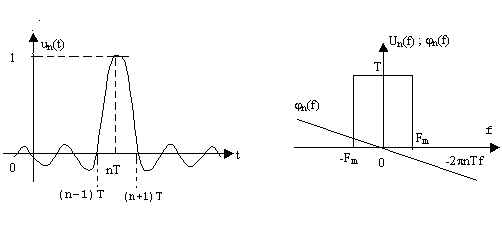
Рис. 3

Графическая интерпретация ряда Котельникова представлена на рис.4.

Рис. 4

Ряд Котельникова (1) обладает всеми свойствами обобщенного ряда Фурье с базисными функциями u_n(nT), и поэтому определяет функцию s(t) не только в точках отсчета, но и в любой момент времени.

Интервал ортогональности функции u_n равен бесконечности. Квадрат нормы

.

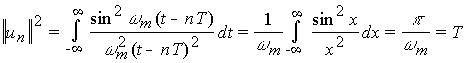Коэффициенты ряда, определяемые по общей формуле для ряда Фурье, равны (с использованием равенства Парсеваля):

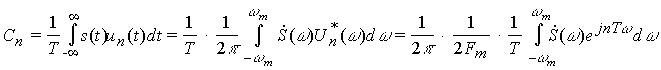
Так как

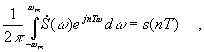
следовательно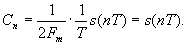

При ограничении спектра сигнала конечной наивысшей частотой ряд (1) сходится к функции s(t) при любом значении t.

Если взять интервал Т между выборками меньшим, чем 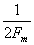, то ширина спектра базисной функции будет больше ширины спектра сигнала, следовательно точность воспроизведения сигнала будет выше, особенно в случаях когда спектр сигнала не ограничен по частоте и наивысшую частоту F_m приходится выбирать из энергетических или информационных соображений, оставляя неучтенными “хвосты” спектра сигнала.

При увеличении расстояния между выборками (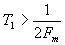) спектр базисной функции становится уже спектра сигнала, коэффициенты C_n будут являться выборками другой функции s ₁ (t), спектр которой ограничен частотой .

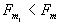Если длительность сигнала T_c конечна, то полоса его частот равна строго бесконечности, т.к. условия конечных длительности и полосы несовместимы. Однако практически всегда можно выбрать наивысшую частоту так, чтобы “хвосты” содержали либо малую долю энергии, либо слабо влияли на форму аналогового сигнала. При таком допущении число отсчетов N на времени Т_с будет равно Т_с/Т, т.е. N=2F_mT_c. Ряд (1) в этом случае имеет пределы 0, N.

Число N иногда называют числом степеней свободы сигнала, или базой сигнала. С увеличением базы точность восстановления аналогового сигнала из дискретного увеличивается.

12. Временные и частотные характеристики линейных радиотехнических цепей. Понятие импульсной характеристики. Понятие переходной характеристики. Понятие входной и передаточной частотной характеристики.

При рассмотрении радиотехнических сигналов было установлено, что сигнал может быть представлен как во временной (динамическое представление), так и в частотной(спектральное представление) областях. Очевидно, при анализе процессов преобразования сигналов цепи также должны иметь соответствующие описания временными или частотными характеристиками.

Начнём с рассмотрения временных характеристик линейных цепей с постоянными параметрами. Если линейная цепь осуществляет преобразование в соответствии с оператором 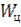и на вход цепи подаётся сигнал 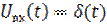в виде дельта-функции (на практике очень короткий импульс), то выходной сигнал (реакция цепи)

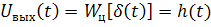(5.5)

называется импульсной характеристикой цепи. Импульсная характеристика составляет основу одного из методов анализа преобразования сигналов, который будет рассмотрен ниже.

Если на вход линейной цепи поступает сигнал 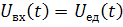, т.е. сигнал вида “единичный перепад”, то выходной сигнал цепи

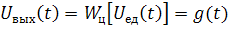(5.6)

называется переходной характеристикой.

Между импульсом и переходной характеристикой существует однозначная связь. Так как дельта-функция (см. подраздел 1.3):

,

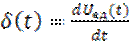то подставляя это выражение в (5.5), получим:

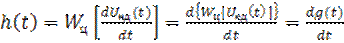. (5.7)

В свою очередь переходная характеристика

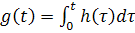. (5.8)

Перейдём к рассмотрению частотных характеристик линейных цепей. Применим к входному и выходному 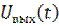сигналам прямое преобразование Фурье

,

.

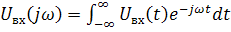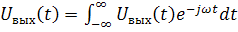Отношение комплексного спектра выходного сигнала к комплексному спектру входного сигнала называется комплексным коэффициентом передачи

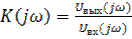(5.9)

Из этого следует, что

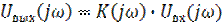. (5.10)

Таким образом, оператором преобразования сигнала линейной цепью в частотной области служит комплексный коэффициент передачи.

Представим комплексный коэффициент передачи в виде

, (5.11)

где и 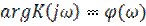соответственно модуль и аргумент комплексной функции 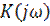. Модуль комплексного коэффициента передачи 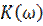как функция частоты называется амплитудно-частотной характеристикой (АЧХ), а аргумент 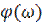– фазочастотной характеристикой (ФЧХ). Амплитудно-частотная характеристика является чётной, а фазочастотная характеристика – нечётной функцией частоты .

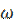Врменные и частотные характеристики линейных цепей связаны между собой преобразованием Фурье

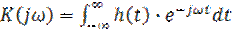, (5.12)

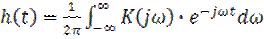, (5.13)

что вполне объяснимо, поскольку они описывают один и тот же объект – линейную цепь.

13. Анализ воздействия детерминированных сигналов на линейные цепи с постоянными параметрами. Временной, частотный, операторный методы.