Принцип Даламбера для материальной точки

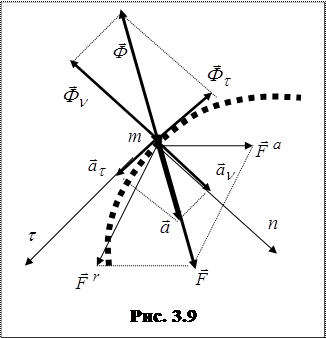Принцип Даламбера связан с понятием силы инерции. Даламберовой силой инерции материальной точки называется вектор , равный произведению массы точки на ее ускорение и направленный в сторону, противоположную ускорению точки: (рис. 3.9).

В частности, при криволинейном неравномерном движении точки (рис. 3.9) даламберова сила инерции находится по составляющим: касательная сила инерции - направлена по касательной к траектории точки противоположно касательному ускорению ; нормальная сила инерции (иногда называют центробежной силой) - направлена по главной нормали противоположно нормальному ускорению .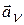

Если к геометрической сумме (рис. 3.9) всех активных сил 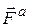и, для несвободной точки, реакций связей добавить даламберову силу инерции 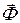, получится уравновешенная система сил: 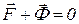или

.

В этом и заключается принцип Даламбера для материальной точки: в каждый данный момент времени при движении материальной точки геометрическая сумма всех активных сил, реакций связей и силы инерции материальной точки равна нулю.

Серьезное преимущество принципа Даламбера при решении задач динамики точки состоит в том, что уравнения движения точки составляются в форме уравнений равновесия. Например, исследовать скольжение тела по наклонной плоскости (см. п. 3.7.4, рис. 3.7) можно с помощью принципа Даламбера. Тогда из векторного равенства в проекции на ось x получится такое же уравнение, как при решении задачи другими методами (п. 3.7.4).

Date: 2015-08-15; view: 415; Нарушение авторских прав