Теңдеулерін интегралдау

Материялық нүктенің инерциалдық санақ жүйесіндегі орнын радиус-вектормен анықтаймыз. Нүктеге әсер ететін күш жалпы жағдайда t уақытқа, нүктенің орнына, яғни радиус-векторға және нүктенің 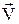жылдамдығына тәуелді болады, яғни 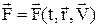. Егер нүктенің үдеуі , ал жылдамдығы екенін ескерсек, Ньютонның екінші заңы немесе нүкте динамикасының негізгі теңдеуі былай жазылады:

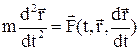. (3.2.4)

Бұл теңдеу векторлық түрдегі нүкте қозғалысының дифференциалдық теңдеуі деп аталады.

(3.2.4) теңдеуі декарттық координата жүйесінің өстеріне проекцияланған үш скалярлық теңдеуге пара-пар:

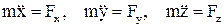. (3.2.5)

Бұл теңдеулер материялық нүкте қозғалысының декарттық координата өстеріне проекцияланған дифференциалдық теңдеулері деп аталады.

Егер жанама үдеу 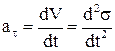, нормаль үдеу , ал толық үдеудің бинормальға проекциясы екенін ескерсек, табиғи өстерге проекцияланған нүкте қозғалысының дифференциалдық теңдеулерін аламыз:

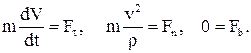(3.2.6)

Соңғы өрнектен материялық нүктені қозғалысқа келтіретін күштің жанасушы жазықтықта жататынын көреміз.

Нүкте қозғалысының дифференциалдық теңдеулері (3.2.5) және (3.2.6) түрінде жиі қолданылады.

Нүкте динамикасының екінші мәселесінің шешуі оның қозғалысының (3.2.5) дифференциалдық теңдеулерін интегралдауға тіреледі Алдымен бұл теңдеулерді төмендегідей етіп жазамыз:

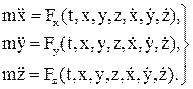(3.2.7)

(3.2.7) теңдеулері x, y, z белгісіз функцияларға қатысты екінші ретті үш дифференциалдық теңдеулер жүйесін береді.

Біз осы теңдеулер жүйесін интегралдап, С₁,С₂,…,С₆ алты интегралдау тұрақтыларына тәуелді жалпы шешімін алдық делік:

(3.2.8)

Интегралдау тұрақтылары әртүрлі мәнге ие бола алады, сондықтан бірдей күш әсер ететін нүкте түрлі қозғалыс жасай алады. Сонымен, нүкте қозғалысының нақты заңын анықтау үшін тек күштің берілуі жеткіліксіз екен. (3.2.8) шешімі нақты мәселеге сәйкес болу үшін қозғалыстың бастапқы шарттарын беру қажет, яғни нүктенің бастапқы орны мен бастапқы жылдамдығын беру керек.

Егер 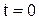бастапқы уақыт болса, осы уақыттағы координаталар мен жылдамдықтар нүкте қозғалысының бастапқы шарттары деп аталатын болады:

t=0: (3.2.9)

(3.2.9) бастапқы шарттар (3.2.8) шешімдері мен олардың бірінші туындыларына қойылады:

(3.2.10)

Осылай алынған теңдеулерден интегралдау тұрақтылары табылады:

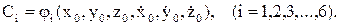(3.2.11)

Табылған тұрақтыларды (3.2.8) жалпы шешімге қойып, берілген бастапқы шарттарға сәйкес келетін есептің шешуін алатын боламыз.

Өзіндік бақылау сұрақтары:

1. Динамика нені зерттейді?

2. Ньютонның заңдары.

3. Еркін және еркін емес нүкте үшін динамиканың екі негізгі мәселесі.

4. Бастапқы шарттар және оларды қолдану.

Date: 2015-08-15; view: 1264; Нарушение авторских прав