
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Четырехмерное пространство - время. Мир Минковского
|
|
Существование интервала, инвариантного к преобразованию инерциальных систем отсчета, обусловлено прежде всего свойствами электромагнитного поля, постоянством скорости света в разных системах отсчета. Значение интервала зависит как от пространственных, так и от временной координат события. Это позволяет рассматривать множество всевозможных значений координат и моментов времени, умноженных на скорость света, как четырехмерное пространство точек или пространство векторов, в котором заданы интервалы,, т. е. своеобразные расстояния между парами физических событий. Особенностью этих расстояний является их постоянство при переходе из одной системы отсчета в другую.
В механике материальных точек, механике Галилея — Ньютона, неизменными величинами при переходе из одной системы отсчета в другую являлись длины отрезков и промежутки времени. В СТО длина отрезка и промежуток времени не будут сохраняться при переходе из одной системы отсчета в другую, так как эти величины входят составными частями в интервал, который остается неизменным, хотя его отдельные части, пространственная и временная, будут изменяться.
При такой геометрической интерпретации многообразию физических событий сопоставляется четырехмерное пространство, называемое часто пространством Минковского, 4-пространством, или, коротко, миром Минковского, в котором каждому физическому событию сопоставляется точка, имеющая четыре координаты, — так называемая 4-тонка или мировая точка, а каждому движению — мировая линия в 4-пространстве. Расстояние между двумя мировыми точками — интервал — представляет собой инвариантную величину. Если расстояние между точками в трехмерном геометрическом пространстве может быть только положительной величиной, то величина квадрата интервала может быть нулевой, как, например, для электромагнитных волн, положительной или отрицательной, причем при всех преобразованиях системы отсчета квадрат интервала не может изменять свой знак. Это означает, что скорость света является максимальной скоростью движения частиц, так как в противном случае с этой частицей можно связать такую систему отсчета, в которой квадрат интервала поменяет свой знак на противоположный.
Квадрат интервала легко выразить через квадраты пространственных и временной координат. Знак квадрата интервала мы выбрали таким образом, чтобы он был положительным для покоящейся частицы. Ограничимся для простоты рассмотрением одной пространственной координаты.
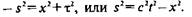
|
| Тогда с учетом выбора знака для квадрата интервала можно записать следующее выражение: |
Как видно из этого выражения, s2 может быть как положительной, так и отрицательной или равной нулю величиной. В первом случае интервал называется времениподобным, во втором — пространственноподобным, в третьем — светоподобным.
Интересно заметить, что временная последовательность пары событий, разделенных времениподобным интервалом, не зависит от выбранной системы отсчета. В этом случае более позднее событие будет наступать позже в любой системе отсчета. Причем можно найти такую систему отсчета, в которой эти события будут происходить в одном месте.
Если же события разделены пространственноподобным интервалом, то их порядок следования во времени будет зависеть от той системы отсчета, где эти события рассматриваются. В частности, для любой пары событий с пространственноподобным интервалом всегда можно найти такую систему отсчета, где эти события будут происходить одновременно.
Date: 2015-07-27; view: 558; Нарушение авторских прав