Пространство и время в СТО. Относительность одновременности в СТО приводит к необходи­мости описания физического состояния материальной точки с по­мощью не только пространственных

Относительность одновременности в СТО приводит к необходи­мости описания физического состояния материальной точки с по­мощью не только пространственных координат, но и временной ко­ординаты, измеряемой часами, связанными с этой материальной точкой. Если начало координат принять за нуль, то координаты про­извольной точки будут связаны друг с другом по определению про­цедуры синхронизации часов простым соотношением

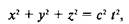
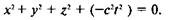
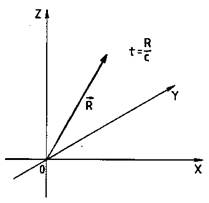
где х, у, z — пространственные координаты материальной точки; t — временная координата этой точки, равная времени распространения света из начала координат до рассматриваемой точки (рис. 93). Анало­гичное соотношение между пространственными и временной координа­тами можно записать для любой материальной точки в выбранной сис­теме координат. Это соотношение можно переписать следующим обра­зом, перенеся произведение c²τ² в левую часть равенства: формально похожее на выражение для квадрата длины вектора в четырехмерном пространстве. Пространство, в котором квадрат одной из проекций радиус-вектора имеет отрицательное значение, называется псевдоевклидовым (что переводится как лжеевклидовое) пространством.

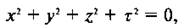
Если выражение в скобках обозначить через τ², то мы получим следующее выражение:

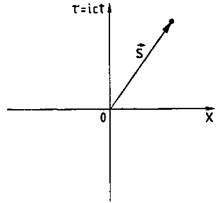
Для упрощения описания со­стояния материальной точки бу­дем считать, что пространствен­ное положение точки характери­зуется только одной координатой х. Тогда квадрат длины вектора в таком пространстве будет равен х² + τ². Для изображения самого вектора введем систему коорди­нат с началом в точке О, по оси абсцисс будем откладывать коор­динату х, по оси ординат — коор­динату ct, умноженную на корень квадратный из минус единицы, или, короче, на мнимую единицу:

i=√-1

Состояние материальной точ­ки определяется ее пространственны­ми и временной координатами

Такой прием позволяет по­лучить правильное выражениедля квадрата люоого вектора в псевдоевклидовом пространстве, изо­бражая его привычным образом с помощью декартовой системы ко­ординат (рис.). Из рисунка видно, что некоторому событию с ко­ординатами (х, τ) соответствует свой радиус-вектор, проведенный из начала координат в точку с названными координатами.

Не нужно забывать, что при таком изображении мы используем

поверхность страницы книги, на которой все векторы подчи­няются соотношениям евклидо­вой геометрии, тогда как векто­ры физических событий подчи­няются соотношениям псевдо­евклидовой геометрии. Это, в частности, проявляется в том, что квадрат длины любого век­тора вдоль временной оси явля­ется отрицательной величиной, а длина вектора вдоль направле­ния распространения света рав­на нулю.

Условное изображение псев­доевклидова пространства	Физические события в псевдо­евклидовом пространстве

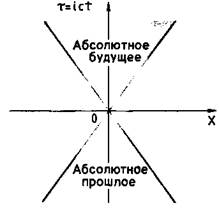
Впервые изображение физи­ческих событий с помощью век-торов в четырехмерном псевдо­евклидовом пространстве пред­ложил немецкий физик Гер­ман Минковский (1864— 1909) в 1908 г. Благодаря идее Минковского о рассмотрении мира физических событий как совокупности векторов четырех­мерного пространства — време­ни мы изменили свой взгляд на окружающий мир. Все физи­ческие события в зависимости от их координат в пространст­ве — времени можно разбить на несколько групп. Две прямые (рис.), являющиеся биссектрисами прямых углов, делят плоскость псевдоевклидового простран­ства (х, τ) на четыре сектора. Любой вектор, направление которого совпадает с направлениями этих биссектрис, имеет нулевую длину и соответствует свету, распространяющемуся в пространстве со скоро­стью с. Любой радиус-вектор, проведенный в одну из точек верхнего сектора между двумя биссектрисами, соответствует событию, проис­ходящему в будущем по сравнению с событием в начале координат. Любой радиус-вектор нижнего сектора соответствует событиям про­шлого по сравнению с событием начала координат. События на оси абсцисс являются одновременными событию в начале координат. Все точки этой оси соответствуют привычному для нас геометрическому пространству классической механики.

Рассмотрим, как следует изображать множество физических со­бытий при переходе в штрихованную систему отсчета, движущуюся относительно нештрихованной со скоростью v вдоль положительно­го направления оси ОХ. Прямая линия, проведенная через начало координат нештрихованной системы отсчета так, чтобы ее угол наклона к оси ординат соответствовал скорости движения штрихо­ванной системы отсчета, будет осью времени штрихованной систе­мы. Применяя процедуру синхронизации часов в штрихованной системе отсчета, получим в качестве совокупности одновремен­ных событий в штрихованной системе ось О'Х' повернутую отно­сительно оси ОХ на такой же угол, что и ось O'τ' относительно оси Оτ.

Таким образом, геометрические пространства, рассматривае­мые как множества одновременно происходящих событий, в штрихованной и нештрихованной системах не совпадают друг с другом.

С другой стороны, при переходе от штрихованной системы от­счета к нештрихованной и обратно сохраняются такие величины, о существовании которых в классической механике мы просто не зна­ли. Так, например, в штрихованной системе х'² + г'² = 0, так же как и в нештрихованной системе из-за постоянства скорости света в лю­бой системе отсчета. Длина четырехмерного вектора в СТО называ­ется интервалом и обозначается буквой s. Применительно к обсуж­даемому случаю можно сказать, что интервалы с нулевым значени­ем сохраняются при переходе из нештрихованной системы отсчета в штрихованную. Оказывается, что это свойство интервалов имеет об­щий характер и справедливо для любых интервалов. Это свойство интервалов следует из постулатов СТО. Чтобы интервал был поло­жительной величиной для частиц, движущихся со скоростями, мень­шими скорости света, х²+τ² приравнивают к s². Интервал, таким об­разом, аналогичен длине отрезка в геометрии Евклида. Значение ин­тервала, подобно длине отрезка, не меняется при различных преоб­разованиях системы координат.

Date: 2015-07-27; view: 388; Нарушение авторских прав