
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Количественные характеристики надежности
|
|
Предварительно рассмотрим понятие “случайная величина”.
Случайная величина - величина, которая в результате опыта может принять то или иное значение, причём заранее неизвестно, какое именно.
Примеры случайной величины:
1) Интервал времени между соседними отказами ЭВМ;
2) Интервал времени от начала работы изделия до первого отказа или время безотказной
работы;
3) Число деталей, изготовленных рабочим в единицу времени.
Обозначим через T - время безотказной работы изделия (интервал времени от начала работы изделия до первого отказа). T - случайная величина. Величина T также называется наработка на отказ изделия. t - возможные значения случайной величины T.
Введём понятие “вероятность безотказной работы”.
P(t) = P(T ≥ t) - вероятность того, что время безотказной работы изделия будет больше или равно некоторому значению t. Другими словами, вероятностью безотказной работы называется вероятность того, что при заданных условиях эксплуатации в течении интервала времени t не возникнет отказа, т.е.система будет работоспособна.
Вероятность отказа:
q(t) = P(T < t) = 1− P(t)
q (t) - вероятность того, что время безотказной работы изделия меньше некоторого заданного значения t.
Другими словами, вероятностью отказа является вероятность того, что в течении заданного времени произойдёт хотя бы один отказ.
Функция q (t) представляет собой функцию распределения случайной величины Т.
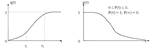
Рассмотрим события А, В, С.
Событие А: T < t2; 0 T
Событие В: T < t1; 0 T
Событие С: t1 ≤ T < t2; 0 T
События В и С несовместные события (в опыте не могут появиться вместе).
А = В + С; P(A) = P(B) + P(С);откуда P(С) = P(A) - P(B); P(A) = P(T < t2); P(B) = P(T < t1);
P(C) = P(t1 ≤ T < t2);Следовательно P(t1 ≤ T < t2) = P(T < t2) - P(T < t1);
или P(t1 ≤ T < t2) = q(t2) - q(t1);
Введём в рассмотрение событие А. Событие А означает, что T ≥ t, т.е. в интервале времени
от 0 до t отказа не произойдёт. Введём в рассмотрение событие A. Событие A означает, что T < t, т.е в интервале времени от 0 до t произойдёт отказ. Из теории вероятностей известно, что сумма вероятностей противоположных событий равна единице, т.е. P(A) + P (A) = 1;
P(A) = P(T ≥ t); P(A) = P(T<t); Следовательно P(T ≥ t) + P(T < t) = 1 или P(t) + q(t) = 1
Для вероятности безотказной работы справедливо приближённое соотношение
P(t) ≈ P* (t), где P* (t) =n(t)/ N)
Здесь n(t) - число изделий, не отказавших к моменту времени t;
N - число изделий, поставленных на испытания.
Испытания изделий должны проводиться при одинаковых условиях так, чтобы отказы
изделий были независимы друг от друга.
Для вероятности отказа справедливо приближённое равенство q(t) ≈ q* (t); где q(t)=(N- n(t))/N.
7. экспериментальная оценка.
Для решения теоретических и практических задач надёжности необходимо знать законы распределения исходных случайных величин. При оценке надёжности изделий может решаться задача определения по данным эксплуатации или специальных испытаний среднего времени безотказной работы mt, среднего времени восстановления mtB
Рассмотрим случайную величину Т - время безотказной работы. При эксплуатации или
испытаниях изделий в течении определённого времени случайная величина Т может принять
n различных значений. Совокупность этих значений случайной величины Т называется
статистической выборкой объёма n. Эта выборка может использоваться для статистической
оценки закона распределения случайной величины Т.
Приведём пример статистической выборки для 10 однотипных изделий.
Номер изделия, i 1 2 3 4 5 6 7 8 9 10
Время безотказной работы i-го изделия, 200 350 600 450 400 400 500 450 550 350 час.
В данном случае n = 10.
При большом числе n удобнее перейти от статистической выборки к статистическому ряду.
Определяем диапазон значений случайной величины Т.
R = tmax − tmin,
где tmax, tmin - максимальное и минимальное значение случайной величины Т.
Этот диапозон R разбивается на интервалы длины Δt
Δt= R/K, где K- количество интервалов.
Определим частоту попадания в i - й интервалi P= n i/ n.
Определяем статистическую плотность вероятности времени безотказной работы Т: f i=P i/ Δti =P i/Δt
Наглядное представление о законе распределения случайной величины Т дают
статистические графики. Из них самые распространённые: полигон, гистограмма,
статистическая функция распределения.
Date: 2015-07-25; view: 374; Нарушение авторских прав