Математические модели

Математические модели позволяют оценивать характеристики ошибок в программах и прогнозировать их надёжность при проектировании и эксплуатации. Модели имеют вероятностный характер, и достоверность прогнозов зависит от точности исходных данных и глубины прогнозирования по времени. Эти математические модели предназначены для оценки:

- показателей надёжности комплексов программ в процессе отладки;

- количества ошибок, оставшихся невыявленными;

- времени, необходимого для обнаружения следующей ошибки в функционирующей программе;

- времени, необходимого для выявления всех ошибок с заданной вероятностью.

В настоящее время предложен ряд математических моделей, основными из которых являются:

- экспоненциальная модель изменения ошибок в зависимости от времени отладки;

- модель, учитывающая дискретно - понижающуюся частоту появления ошибок как линейную функцию времени тестирования и испытаний;

- модель, базирующаяся на распределении Вейбула;

- модель, основанная на дискретном гипергеометрическом распределении.

При обосновании математических моделей выдвигаются некоторые гипотезы о характере проявления ошибок в комплексе программ. Наиболее обоснованными представляются предположения, на которых базируется первая экспоненциальная модель изменения ошибок в процессе отладки и которые заключаются в следующем:

1. Любые ошибки в программе являются независимыми и проявляются в случайные моменты времени.

2. интенсивность проявления ошибок при реальном функционировании программы зависит от среднего быстродействия ЭВМ.

3. Выбор отладочных тестов должен быть представительным и случайным

4. Ошибка, являющаяся причиной искажения результатов, фиксируется и исправляется после завершения тестирования либо вообще не обнаруживается.

Из этих свойств следует, что при нормальных условиях эксплуатации количество ошибок, проявляющихся в некотором интервале времени, распределено по закону Пуассона. В результате длительность непрерывной работы между искажениями распределена экспоненциально.

Предположим, что в начале отладки комплекса программ при τ = 0 в нём содержалось N0 ошибок. После отладки в течении времени τ осталось n0 ошибок и устранено n ошибок n0 + n = N0). При этом время τ соответствует длительности исполнения программ на вычислительной системе (ВС) для обнаружения ошибок и не учитывает простои машины, необходимые для анализа результатов и проведения корректировок. Интенсивность обнаружения ошибок в программе dn/dτ и абсолютное количество устранённых ошибок связываются уравнением

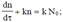
где k - коэффициент.

Время безотказной работы программ до отказа T или наработка на отказ, который рассматривается как обнаруживаемое искажение программ, данных или вычислительного процесса, нарушающее работоспособность, равно величине, обратной интенсивности обнаружения отказов (ошибок):

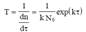
В процессе отладки и испытаний программ для повышения наработки на отказ от T1 до T2

необходимо обнаружить и устранить Δn ошибок. Величина Δn определяется соотношением:

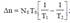
затрат времени Δτ на проведение отладки

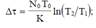
Вторая модель построена на основе гипотезы о том, что частота проявления ошибок (интенсивность отказов) линейно зависит от времени испытания ti между моментами обнаружения последовательных i - й и (i - 1) - й ошибок.

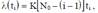
где N0 - начальное количество ошибок; K - коэффициент пропорциональности. Для оценки наработки на отказ получается выражение, соответствующее распределению Релея:

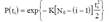
Отсюда плотность распределения времени наработки на отказ

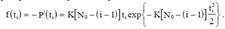
Особенностью третьей модели является учёт ступенчатого характера изменения надёжности при устранении очередной ошибки. В качестве основной функции рассматривается распределение времени наработки на отказ P(t). Если ошибки не устраняются, то интенсивность отказов является постоянной, что приводит к экспоненциальной модели для распределения:

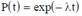
Отсюда плотность распределения наработки на отказ T определяется выражением:

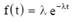
где t > 0, λ > 0 и 1/λ - среднее время наработки на отказ, т.е. Тср=1/λ. Здесь Тср – среднее время наработки на отказ.

Распределение Вейбулла достаточно хорошо отражает реальные зависимости при расчёте

функции наработки на отказ.

Основные понятия вероятности

Событие, вероятность события.

Частота или статистичская вероятность

Случайная величина

Невозможные и достоверные события

Date: 2015-07-25; view: 684; Нарушение авторских прав