Эллипсоид как фигура равновесия

Как мы уже говорили, внутри однородного эллипсоида, как и для шара, сила притяжения подчиняется закону Гука: она прямо пропорциональна отклонению материальной точки от положения равновесия. В теории потенциала доказано, что силовая функция для внутренней точки имеет вид 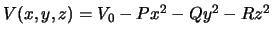. Тогда компоненты силы притяжения пропорциональны координатам притягиваемой точки 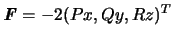. Здесь 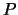, , 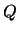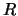и 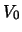-- постоянные, зависящие от плотности и параметров эллипсоида и не зависящие от координат точки. Приведем эти формулы без вывода

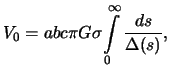
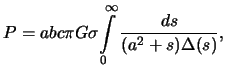
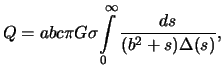
(4.3)

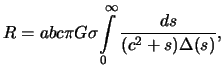
где

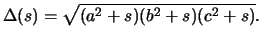
Если притягиваемая материальная точка -- внешняя, то для нее силовая функция сохраняет тот же вид, но 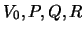перестают быть постоянными, а зависят от координат точки. Для их вычисления справедливы те же интегралы, что и для внутренней точки, но нижний предел не нуль, а величина 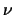, которая выбирается таким образом, чтобы эллипсоид

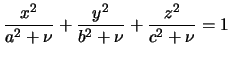
проходил через заданную внешнюю точку.

Потенциал тяжести от потенциала притяжения отличается тем, что аддитивно содержит потенциал центробежной силы 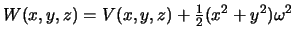. Подставляя сюда выражение для потенциала притяжения эллипсоида, получим

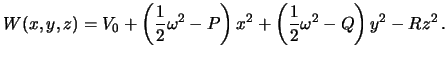
(4.4)

Если поверхность эллипсоида является поверхностью уровня, то такой эллипсоид будет гидростатически равновесным. Уравнением уровенной поверхности будет 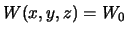, где 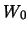-- постоянная величина. Возникает вопрос, можно ли подобрать такую угловую скорость вращения для трехосного эллипсоида с заданными полуосями, чтобы его поверхность оказалась поверхностью уровня? Нетрудно убедиться, что нельзя.

Уравнением трехосного эллипсоида в данном случае будет выражение

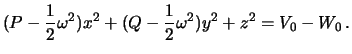
(4.5)

Определим большие полуоси

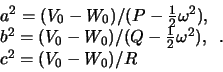
(4.6)

Очевидно, что если из первого уравнения мы определим угловую скорость, то совсем не обязательно, чтобы эта угловая скорость удовлетворяла второму уравнению. Тем не менее специалистами в области теории фигур равновесия небесных тел доказано существование равновесных трехосных эллипсоидов, которые получили название эллипсоидов Якоби.

Date: 2015-07-25; view: 697; Нарушение авторских прав