Сфероид Клеро

Сфероидом в геодезии называют поверхность вращения, близкую к сфере. В первом приближении в качестве уравнения сфероида можно принять

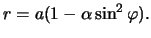
(4.9)

Очевидно, что на экваторе 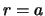, а на полюсах 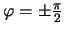, 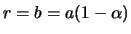. Фигура, уравнение которой удовлетворяет формуле (4.9) обладает сжатием: полярный радиус ее меньше экваториального. Из определения следует, что .

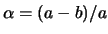Установим связь между коэффициентом 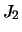и сжатием планеты. Из формулы (3.18) следует, что потенциал притяжения равен

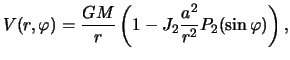
а потенциал тяжести --

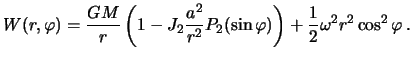
(4.10)

В приведенной формуле мы ограничились лишь коэффициентом 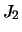, отбросив все остальные мультипольные моменты, так как в случае гидростатически равновесной фигуры, они будут иметь более высокий порядок малости, чем постоянная .

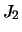Введем обозначение 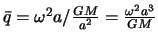. Новая малая величина есть, грубо говоря, отношение центробежной силы на экваторе к силе притяжения. Следовательно 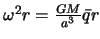. Подставим полученное выражение в (4.10) и вынесем за общие скобки отношение :

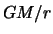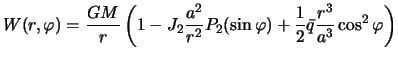
(4.11)

Приравнивая полученное выражение постоянной 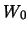, получим уравнение сфероида.

Теорема Клеро устанавливает связь между параметрами сфероида, силой тяжести на его поверхности и коэффициентами разложения гравитационного потенциала.

Сжатие сфероида Клеро.

Сравним формулу (4.11) с (4.9). Учитывая, что 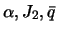-- малые величины, запишем приближенное равенство

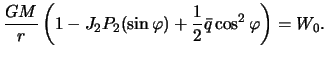
Решим полученное выражение относительно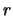

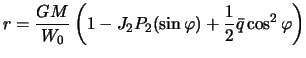
(4.12)

Чтобы отождествить полученную формулу с уравнением сфероида (4.9), примем во внимание, что

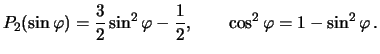
Поставляя эти равенства в (4.12), получим

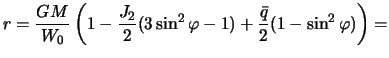
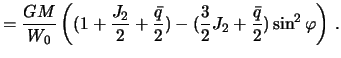
Сравнивая полученное выражение с (4.9) и учитывая, что 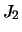и 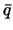-- малые величины, получим

(4.13)

Отсюда определяем постоянную

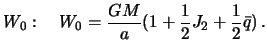
(4.14)

Итак, первая часть теоремы Клеро устанавливается связь между сжатием равновесной планеты с первым коэффициентом зональной гармоники разложения гравитационного потенциала и угловой скоростью вращения планеты.

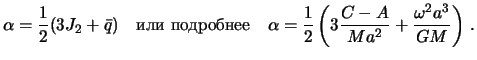
(4.15)

Вторая часть теоремы Клеро определяет зависимость силы тяжести на поверхности равновесной планеты от широты.

Сила тяжести на поверхности сфероида Клеро.

Вернемся снова к формуле потенциала тяжести для сфероида (4.11). Для того, чтобы получить силу тяжести нам нужно потенциал продифференцировать по нормали к поверхности уровня. Однако, поскольку наш сфероид мало отличается от сферы, дифференцирование по нормали мы заменим дифференцированием по радиус-вектору, что значительно проще.

Обозначив производную по радиус-вектору буквой 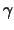, получим

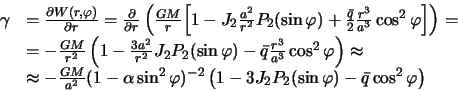
С точностью до малых величин первого порядка будем иметь

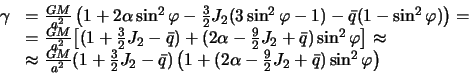
Сила тяжести на экваторе, согласно полученной формуле, равна

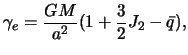
(4.16)

а для любой широты

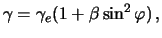
(4.17)

где 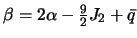. С помощью (4.15) исключим 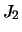: 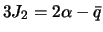, то есть

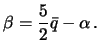
(4.18)

здесь .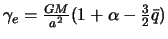

Формулами (4.17) и (4.18) мы и завершим изложение теоремы Клеро.

Date: 2015-07-25; view: 922; Нарушение авторских прав