Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Два предела сжатия для фигур равновесия
|
|
Коснемся сначала истории нашего вопроса. И.Ньютон (1643-1727) для объяснения явления, которое заметили многое астрономы, отъезжающие в экспедиции для наблюдений солнечного затмения в экваториальную зону, астрономические часы маятникового типа отстают по сравнению с Парижской обсерваторией, где они строго выверялись, на 2,5 минуты в сутки. Ньютон предположил, что виной тому служит эллипсоидальная форма Земли и, естественно, ее суточное вращение. Предполагая, что Земля -- однородный эллипсоид вращения, он получил, что сжатие земного эллипсоида должно быть равным 1,25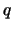 
=1:230.
Современник Ньютона Гюйгенс (1629-1695) решает ту же задачу, но другим путем. Он предположил, что силы притяжения направлены к центру, а эллипсоидальность поверхности уровня возникает только за счет центробежной силы. Таким образом, если Ньютон в качестве фигуры равновесия брал эллипсоид Маклорена, то Гюйгенс -- фигуру, которую мы назвали "планетой Роша". Он получил, что сжатие равно 0.5 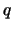= 1:576. Результат, который значительно отличается Ньютоновской оценки сжатия.
Вернемся к теории Клеро. Согласно его теории сжатие равновесной планеты должно быть равно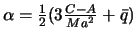 
. Первый предел сжатия получим, если примем Земли однородным двухосным эллипсоидом, для которого 
, 
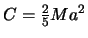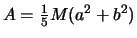. Отсюда 
.
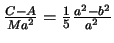Но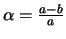 
, 
, 
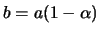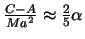. Следовательно 
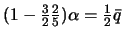и, наконец,
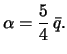
| (4.19) |
Мы получили то же значение, что и Ньютон, правда с точностью до первой степени сжатия.
Второй предел сжатия, мы получим, если будем считать все притягивающие массы шаром, тогда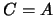 
и
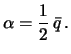
| (4.20) |
Таким образом. реальное сжатие лежит между этими двумя пределами
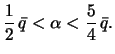
Для иллюстрации сказанного приведем сжатия некоторых планет Солнечной системы, а также их возможные предельные значения
| Таблица. Сжатия планет | ||||
| Название планеты | сжатие | |||
| по Ньютону | по Гюйгенсу | реальное | ||
| Земля | 1:230 | 1:576 | 1:297 | |
| Марс | 1:174 | 1:434 | 1:192 | |
| Юпитер | 1:9,4 | 1:23,5 | 1:15 | |
| Сатурн | 1:5,1 | 1:12,8 | 1:10 | |
| Уран | 1:10,6 | 1:26,6 | 1:14 |
Сравнивая значения сжатия, мы видим, что фигура планеты в значительно степени зависит от ее внутреннего строения. Планеты Земля и Марс весьма далеки от того строения, которое принял Гюйгенс: планета имеет компактное твердое притягивающее тело, окруженное рыхлой оболочкой. По величине сжатия можно судить о том, что к такой модели более подходят планеты гиганты.
Приведенные данные взяты из книги акад. А.А. Михайлова "Курс гравиметрии и теории фигуры Земли", опубликованной в 1939 году. Современные данные могут несколько отличаться от приведенных, хотя общая картина не изменится.
Date: 2015-07-25; view: 572; Нарушение авторских прав