Гравитационный потенциал шара

Все планеты Солнечной системы имеют сферическую форму. Поэтому имеет смысл определить гравитационный потенциал шара. Для упрощения задачи, мы будем предполагать, что плотность шара зависит только от расстояния до его центра Нетрудно убедиться, что такой шар притягивает точно так же, как и материальная точка с массой равной массе шара и помещенная в его центр. Чтобы в этом убедиться, необходимо для формулы (3.4) выбрать такую систему координат, с помощью которой было бы удобно выполнять интегрирование.

Для начала, представим себе, что точка 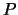находится вне шара. Соединим эту точку с центром шара (точка О), полученный радиус-вектор обозначим через 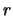. Радиус-вектор элемента массы будем обозначать буквой . Следовательно расстояние между элементом массы и точкой 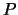, которое мы обозначили греческой буквой , будет иметь вид , где -- угол с вершиной в центре шара, образованный радиус-векторам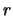и и 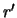. Наконец, элемент массы определяется произведением плотности на объем элементарно малого параллелепипеда со сторонам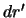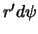и , , и 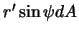. Здесь мы ввели еще одну степень свободы -- поворот вокруг оси 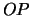на угол 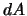. Таким образом,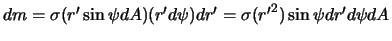

Теперь вместо формулы (3.4) записать

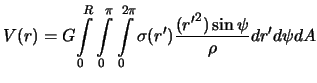
(3.5)

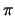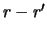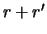Заменим переменную интегрирования на . Определим пределы интегрирования. Очевидно, что вместо 0 и нужно взять и , а 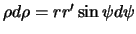. Переменную 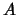подынтегральное выражение не содержит, поэтому внутренний интеграл легко берется. Вместо (3.5) теперь будем иметь

(3.6)

Нетрудно догадаться, что 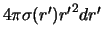есть масса бесконечно тонкой сферы 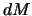, поэтому

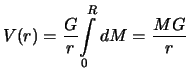
(3.7)

Таким образом, мы пришли к очень важному выводу: шар со сферически симметрично распределенной массой притягивает так же, как и материальная точка с массой равной массе шара и помещенной в его центре.

Date: 2015-07-25; view: 674; Нарушение авторских прав