Свойства гравитационного потенциала

Отметим некоторые свойства потенциала притяжения.

Гравитационный потенциал тела регулярен на бесконечности:

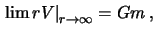
это можно понять, рассуждая следующим образом. Гравитационный потенциал тела, удаленного на большое расстояние от точки, в которой нас интересует значение потенциала, то же, что и потенциал материальной точки, так как все детали строения тела и его форма на больших расстояниях становятся не существенными. Остается лишь масса тела.

Гравитационный потенциал непрерывен вместе со своими первыми производными всюду как вне тела, так и внутри его. Несколько позже, на примере шара, мы это продемонстрируем.

Вторые производные потенциала при переходе через поверхность шара терпят разрыв. Это свойство также покажем на примере шара.

Гравитационный потенциал вне притягивающего тела подчиняется уравнению Лапласа

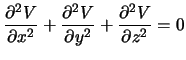
Покажем это. Поскольку 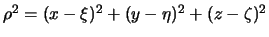, то 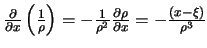, далее 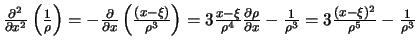. Аналогично

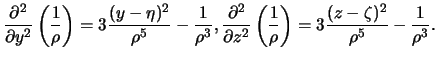
Отсюда следует, что .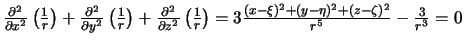

Для записи уравнения Лапласа используют линейный оператор вида

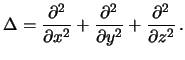
Из только что сделанных выкладок следует, что 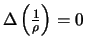. Теперь обратимся к формуле (3.3). Используя операторную форму записи, получим .

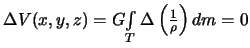Гравитационный потенциал тела в точке, расположенной внутри тела подчиняется уравнению Пуассона

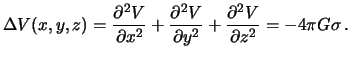
Легко видеть, что уравнение Пуассона является обобщением уравнения Лапласа, ибо в частном случае, в точке, где плотность 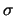равна нулю, то есть где нет гравитирующих масс, потенциал подчиняется уравнению Лапласа.

Date: 2015-07-25; view: 564; Нарушение авторских прав