
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Динамические модели
|
|
В предыдущей главе мы рассматривали модели, которые являются статическим отражением систем в определенные моменты времени. В этом смысле рассмотренные варианты модели «черного ящика», модели состава и структурной модели называют статическими моделями, что подчеркивает их неподвижность.
Следующий шаг в исследовании системы состоит в том, чтобы понять и описать, как система «работает», выполняя свое предназначение. Такие модели должны описывать поведение системы, фиксировать изменения, происходящие с течением времени, улавливать причинно-следственные связи, адекватно отражать последовательность протекаемых в системе процессов и этапность ее развития. Такого рода модели называют динамическими. При исследовании конкретной системы необходимо определить направление возможных изменений ситуации. Если такой перечень будет исчерпывающим, то он характеризует число степеней свободы, а значит, достаточен для описания состояния системы. Как оказалось, динамические модели делятся на такие же типы, как статические («черного ящика», состава и «белого ящика»), только элементы этих моделей имеют временной характер.
2.4.1. Динамическая модель «черного ящика»
При математическом моделировании динамической системы ее конкретная реализация описывается в виде соответствия между возможными значениями некоторой интегральной характеристики системы с и моментами времени t. Если обозначить через С — множество возможных значений с, а через Т — упорядоченное множество моментов времени t, то построение модели динамической системы равносильно построению отображения
Г->С:с(t)ϵСͭͭ,
где Сͭ — значение интегральной характеристики в точке t ϵ [0, Т].
В динамической модели «черного ящика» предполагается разбиение входного потока х на две составляющие: и — управляемые входы, y — неуправляемые входы (рис 2.9).
Таким образом, она выражается совокупностью двух процессов:
Хͭ = {u(t), y(t)}; u(t)eU; y(f)eK;
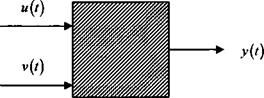
Рис. 2.9. Динамическая модель «черного ящика»
Если даже считать y(t) результатом некоторого преобразования Ф процесса х(t), т.е. y(t) = Ф[х(t)], то в модели «черного ящика»
предполагается, что это преобразование неизвестно.
Из данного типа моделей в наибольшей мере изучены так называемые безынерционные системы. Они не учитывают фактора времени и работают по схеме «если-то». Например: если воду нагреть до
100° С, то она закипит. Или: если вы правильно авторизовали свою кредитную карту, то банкомат вам сразу выдаст затребованную сумму денег. То есть следствие вступает в силу сразу за причиной.
Определение 1. Динамическая система называется безынерционной, если она мгновенно преобразует вход в выход, т.е. если y(t)
является функцией только х(t) в тот же момент времени.
Поиск неизвестной функции у(/) = Ф(х(t)) осуществляется посредством наблюдения входов и выходов исследуемой системы. По существу, эта задача о переходе от модели «черного ящика» к модели «белого ящика» по наблюдениям входов и выходов при наличии информации о безынерционности системы.
Однако класс безынерционных систем весьма узок. В экономике такие системы очень большая редкость. Разве только отдельные биржевые операции с некоторой натяжкой можно причислить к классу безинерционных.
При моделировании экономических систем необходимо помнить, что в них всегда присутствует задержка и, более того, следствие (результат) может проявиться совсем не в том месте, где его ожидали. Таким образом, имея дело с экономическими системами, нужно быть готовым к тому, что последствия могут отстоять от вызвавшей их причины во времени и пространстве.
Например, если в фирме отдел сбыта пустит на самотек предпродажное обслуживание и сконцентрирует все свои силы на продажах, пострадает отдел гарантийного обслуживания. Но это проявится не сразу, а спустя определенное время. На лицо проявление следствия «не там и не в то время». Или: для изменения покупательских пристрастий может потребоваться несколько недель рекламной кампании, и не обязательно ощутимые перемены начнутся сразу же после ее окончания.
Обратная связь действует по цепочке причинно-следственных связей, образующих замкнутый контур, и требуется время, чтобы его обойти. Чем большей динамической сложностью обладает система, тем больше нужно времени на то, чтобы сигнал обратной связи пробежал по ее структуре (сети взаимосвязей). Достаточно одной задержки, чтобы обеспечить сильное запаздывание сигнала.
Определение 2. Время, необходимое для того, чтобы сигнал обратной связи прошел по всем звеньям системы и вернулся в исходную точку, называется памятью системы.
Не только живые системы имеют память. В экономике, например, это ярко демонстрирует процесс вывода на рынок нового товара. Как только на рынке появляется новый товар, пользующийся спросом, сразу находится много желающих его производить. Многие фирмы запускают производство этого товара, и пока существует спрос, наращивают его объемы. Рынок постепенно насыщается, но производители пока этого не ощущают. Когда объем производства превысит некоторое критическое значение, спрос станет падать. Производство товара по определенной инерции еще некоторое время будет продолжаться. Начнется затоваривание складов готовой продукцией. Предложение сильно превысит спрос. Цена на товар упадет. Многие фирмы прекратят производство этого товара. И такая ситуация будет сохраняться до тех пор, пока предложение не упадет до таких значений, что не сможет покрыть существующий спрос. Рынок сразу уловит складывающийся дефицит и отреагирует повышением цены. После этого начнется оживление производства и новый цикл взлета-падения рынка. Так будет продолжаться до тех пор, пока на рынке не останутся несколько производителей, которые либо договорятся между собой, либо интуитивно нащупают квоты производства товара, суммарный объем которых будет соответствовать требуемому соотношению спроса и предложения (рис. 2.10).
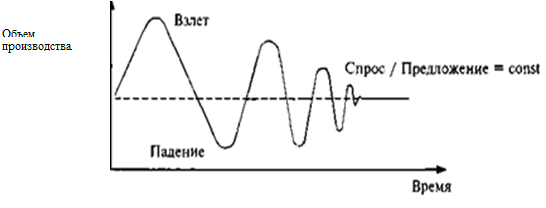 |
Точно так же выглядят графики инфляции и дефляции денежного рынка, расцвета и крахов фондового рынка, пополнения и расходования семейного бюджета. Все дело в том, что причину и следствие разделяет задержка во времени. Все это время система «помнит» как она должна отреагировать на причину. На первых порах кажется, что и следствия-то никакого нет. Но со временем эффект проявляется. Введенные в заблуждение (в нашем примере предприниматели) слишком поздно и слишком сильно реагируют на пики спроса и предложения. А во всем виновата уравновешивающая обратная связь, работающая с задержкой во времени.
Рис. 2.11. Колебание рынка товара
В такой ситуации есть два решения. Во-первых, можно сделать более надежным измерение, осуществляя постоянный или периодический мониторинг рынка. Во-вторых, следует учитывать разницу во времени и стремиться оказаться там где нужно к тому времени, когда сигнал обратной связи успеет пройти через все звенья системы. Когда понимаешь, как осуществляется процесс, появляется возможность изменить ситуацию в желательном направлении.
В очень сложных системах следствие может проявиться спустя очень длительное время. К тому времени, когда оно даст о себе знать, критический порог может миновать и будет уже поздно что- либо исправлять. Особенно наглядно такая опасность просматривается во влиянии промышленных отходов на окружающую среду. То, что мы делаем сейчас, скажется на нашей будущей жизни, когда появятся последствия наших дел. Нашими сегодняшними поступками мы формируем облик будущего.
В облике динамической модели «черного ящика», по существу, ничего не изменится, кроме того, что момент появления выхода у потребуется скорректировать на время задержки ∆, т.е. выход системы примет вид y(t + ∆) (см. рис. 2.10). Однако основная трудность моделирования в том и заключается, чтобы определить величину Д и место, в котором появится у. Наилучшим образом это удается в рамках построения так называемых лаговых моделей, которые изучает математическая статистика.
2.4.2. Динамическая модель состава
В теории систем различают два вида динамики: функционирование и развитие. Под функционированием подразумевают процессы, которые происходят в системе, стабильно реализующей фиксированную цель (функционирует предприятие, функционируют часы, функционирует городской транспорт и т.п.). Под развитием понимают изменение состояния системы, обусловленное внешними и внутренними причинами. Развитие, как правило, связывают с движением систем в фазовом пространстве.
Исследованием функционирования экономических систем заняты специалисты в области экономического анализа. Исходную базу для этого исследования составляют данные бухгалтерского учета, статистической отчетности и статистических наблюдений. В большинстве случаев задача экономического анализа решается аналитическими методами бухгалтерского учета или сводится к построению и реализации корреляционно-регрессионных моделей. Богатейший инструментарий экономического анализа изучается в рамках ряда дисциплин цикла «Бухгалтерский учет и статистика».
Развитие в большинстве случаев обусловлено изменением внешних целей системы. Характерной чертой развития является то, что существующая структура перестает соответствовать новым целям и для обеспечения необходимого соответствия приходится изменять структуру системы, т.е. осуществлять ее реорганизацию. Экономические системы (предприятия, организации, корпоративные образования) в условиях рыночной экономики для выживания в конкурентной борьбе должны постоянно находиться в фазе развития. Только постоянное обновление ассортимента выпускаемой продукции или оказываемых услуг, совершенствование технологии производства и методов управления, повышение квалификации и образованности персонала могут обеспечить экономической системе определенные конкурентные преимущества и расширенное воспроизводство.
В данном параграфе, не отрицая значимости фазы функционирования системы, большей частью будем вести речь о фазе ее развития, хотя при расширенном толковании функционирования системы как движения к намеченной цели (плану) приведенные ниже рассуждения вполне применимы к моделированию фазы функционирования системы.
Динамическому варианту модели состава соответствует перечень этапов развития или состояний системы на моделируемом интервале времени. Под состоянием системы будем понимать такую совокупность параметров, характеризующих пространственное положение системы, которая исчерпывающе определяет ее текущее позирование.
Фиксация состояния определяется посредством введения различных переменных, каждая из которых отражает какую-то одну существенную сторону исследуемой системы. В данном случае важна исчерпываемость описания для раскрытия того назначения системы, которое подвергается исследованию в рамках данной модели.
Наиболее наглядно состояние системы определяется через степени свободы. Это понятие введено в механике и означает число независимых координат, однозначно описывающих положение системы. Так, твердое тело в механике есть система с шестью степенями свободы: три линейные координаты фиксируют положение центра масс, а три угловые — положение тела относительно центра масс.
В экономических исследованиях каждую координату (степень свободы) связывают с определенным показателем (количественно измеряемой характеристикой системы). Ключевая задача при этом заключается в том, чтобы обеспечить независимость показателей, отобранных для построения модели системы. Поэтому необходимо глубоко понимать природу экономических явлений и отражающих их показателей, чтобы правильно сформировать базис для построения модели состава экономической системы.
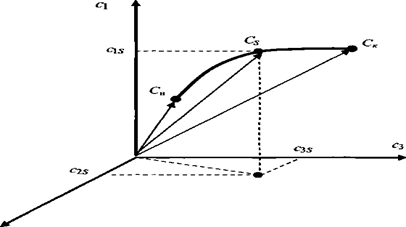 |
Развитие системы есть не привычное перемещение, а некоторая абстракция, описывающая изменение ее состояния. Таким образом, динамические свойства объекта характеризуются через изменение параметров состояния во времени. На рис. 2.12 приведено графическое отображение движения системы в трехмерном пространстве (в теории систем такое пространство называют пространством состояний, или фазовым пространством).
Рис. 2.12. Траектория развития системы
Тогда состояние системы в момент времени ts описывается вектором Cs = (C1s,C2s,C3s). Аналогично описываются ее начальное Сн и конечное Ск состояния, а изменения в системе отображаются некоторой кривой — траекторией развития. Каждая точка этой кривой фиксирует состояние системы в определенный момент времени. Тогда движение системы эквивалентно перемещению точки по траектории С2.
Экстраполируя это описание на случай и независимых координат и помня, что каждая координата (параметр) зависит от времени t, развитие системы можно описать совокупностью функций с1= с1(t), с2=с2(t),..., сn =сn(t), или вектором (с1(t), с2 (t),...,сn =сn(t)), принадлежащим пространству состояний С.
Таким образом, динамическая модель состава системы это не что иное, как упорядоченная последовательность ее состояний, последнее из которых эквивалентно цели системы, т.е.
Сн =С0 —>СJ —>Ct —>...—>СT=Ск,
где Сн — начальное;
Ск — конечное;
С, = (c1 (t), c2 (t),..., сn (t)), t ϵ [0, T] — текущее состояние системы.
Случай, когда строго определены граничные состояния системы, относится к категории простейших, так как далеко не всегда удается описать состояние конкретными значениями. Более общей является ситуация, когда на начальное и конечное состояния системы накладываются некоторые условия. Каждое из условий в пространстве состояний представляется некоторой поверхностью или областью, размерность которой не должна быть больше числа степеней свободы системы. Тогда вектор состояния системы в граничные моменты времени должен находиться на заданной поверхности или в заданной области, что и будет означать выполнение условий.
2.4.3. Динамическая структурная модель
В динамических системах элементы могут вступать в самые разнообразные отношения между собой. А поскольку каждый из них способен пребывать во множестве различных состояний, то даже при небольшом числе элементов они могут быть соединены множеством различных способов. Построить модель такой системы, предусмотрев изменение состояний одних элементов системы в зависимости от того, что происходит с другими ее элементами, — очень непростая задача. Тем не менее современная наука выработала немало подходов к моделированию такого рода систем. На двух из них, которые стали классическими, остановимся подробнее.
Как и в случае статической структурной модели, динамическая структурная модель представляет собой симбиоз динамической модели «черного ящика» и динамической модели состава. Другими словами, динамическая структурная модель должна увязать в единое целое вход в систему X = {х(t)} = {u(t),v(t)}, u(t)ϵu, v(t)ϵV, промежуточные состояния
Ct =[C1 (t), C2(t),..., cn(t)], t ϵ[0,T], и выход y={y(t)},
где, U — множество управляемых входов u(t);
U — множество неуправляемых входов v(t);
X = U U X — множество всех входов в систему;
Т — горизонт моделирования системы;
С, — промежуточное состояние системы в момент времени t ϵ [0, T].
В зависимости от того, отображаются промежуточные состояния системы строго определенной упорядоченной последовательностью
Сt (t = 0,1, 2,..., Т) или одной неопределенной функцией Ct = Ф(t, хt), в результате моделирования получают либо динамическую структурную модель сетевого типа, либо динамическую структурную модель аналитического типа.
Сетевые динамические модели. В динамической структурной модели сетевого типа для каждой пары соседних состояний системы Сt-1 и Сt (t ϵ [0, T]) задается управляющее воздействие u(t), которое переводит систему из состояния Ct-l в состояние Ct. При этом очевидно, что u(t) на каждом шаге траектории может принимать значения из некоторого множества допустимых управляющих воздействий на этом шаге
Ut: u(t)ϵUt. (2.1)
Таким образом, промежуточное состояние системы в некоторой точке t траектории ее развития записывается следующим образом
Сt=F(Ct-i,u(t)), t ϵ[0,T].
Обозначим через Ct множество всех состояний системы, в которое можно ее перевести из начального состояния C0=CH за t шагов, используя управляющие воздействия u(t) ϵ Ut (t = 0,1, 2,..., t). Множество достижимости Сt определяется с помощью следующих рекуррентных соотношений:
Сt = {Ct: Сt = ƒ(Сt-1, и(t); и(t ϵUt; t = 0,1, 2,...,t}.
В задании на дальнейшее развитие или первоначальную разработку системы указывается перечень допустимых ее конечных состояний, которые должны принадлежать некоторой области
СtϵС-Т. (2.2)
Управление U =(u(1), u(2),..., u{t),..., и(Т)), состоящее из пошаговых управляющих воздействий, будет допустимым, если оно переводит систему из начального состояния Сн = С0 в конечное состояние Ск =СT, удовлетворяющее условию (2.2).
Выведем условия допустимости управления. Для этого рассмотрим последний Т-й шаг. В силу ограниченности множества UT перевести систему в состояние СT ϵ СT можно не из любого состояния CT-1, а лишь из—T-1,Ст-1 G с,
Где, С — множество, удовлетворяющее условию
VCT=1 ϵ C-T-1зu(T)ϵUT: су =/(СУ-1, и(Т))&ст.
Иными словами, чтобы иметь возможность после Т-то шага—г управления выйти в область допустимых состояний С, необходимо—г-1 после (Г — 1) шагов находиться в области С.
Аналогичные множества допустимых состояний с' формируются для всех остальных шагов t = 1, Т — 1.
Для достижения цели построения (развития) системы необходимо выполнение условий
С'ПС'*0, / = 1,Т. (2.3)
В противном случае цель системы не может быть достигнута. Для преодоления этого препятствия потребуется либо изменить—T цель системы, изменив тем самым С, либо расширить область возможных управляющих воздействий ut = 1,Т (в первую очередь на тех шагах траектории системы, на которых не выполняется условие 2.3).
Пусть в результате преодоления (t -1) шагов система перешла в состояние Ct-1. Тогда множество допустимых управляющих воздействий на t-м шаге определяется следующим образом:
U(t) = {u(t): Сt =ƒ(Сt-1, u(t) ϵс-t}. (2.4)
Объединяя (2.1) и (2.4), можно записать условия управляемого целенаправленного развития системы:
U(t)ϵ(t)nU(f) = 1д. (2.5)
Условия (2.5) означают, что управление должно быть возможным по его реализуемости и допустимым по обеспечению выхода системы в заданную область конечных состояний.
Таким образом, построение динамической структурной модели системы сетевого типа заключается в формализованном описании траектории ее развития путем задания промежуточных состояний системы и управляющих воздействий, последовательно переводя щих систему из начального состояния в конечное, соответствующее цели ее развития.
Поскольку из «начала» в «конец», как правило, существует множество путей, определение траектории развития системы можно вести по различным критериям (минимуму времени, максимуму эффекта, минимуму затрат и т.п.). Выбор критерия определяется целью моделирования системы.
Такой подход к моделированию динамических систем, как правило, приводит к построению сетевых моделей разных типов (сетевым графикам, технологическим сетям, сетям Петри и т.п.). Независимо от типа сетевой модели их сущность заключается в том, что они описывают некоторую совокупность логически увязанных работ, выполнение которых должно обеспечить построение некоторой системы (предприятия, дороги, политической партии) или перевода ее в другое состояние, соответствующее новым целям и требованиям времени.
Конкретизация динамических систем на этом, конечно, не заканчивается. Приведенные модели, скорее всего, являются отдельными примерами реальных систем. В классе моделей динамических систем различают еще стационарные модели, мягкие и жесткие модели, которые находят применение при исследовании конкретных прикладных проблем.
Контрольные вопросы
1. Приведите несколько определений системы и содержательную характеристику каждого из них.
2. В чем заключается разница между философской категорией и естественно-научным понятием?
3. Перечислите и проинтерпретируйте основные свойства системы.
4. Что такое эмерджентность системы?
5. Как соотносятся понятия «целостность» и «эмерджентность»?
6. В чем заключается сущность редукционизма? Чем он отличается от системного подхода?
7. В чем заключается разница между внешними и внутренними связями системы?
8. Какое свойство лежит в основе деления систем на открытые и закрытые (замкнутые)?
9. Приведите примеры закрытых экономических систем.
10. С помощью чего обеспечивается устойчивость системы?
11. В чем заключаются внутренняя и внешняя цели системы?
12. Как согласуются внутренняя и внешняя стратегии системы?
13. Как установить границы экономической системы?
14. Назовите причину неудовлетворительности прогнозов, получаемых в результате эконометрического моделирования.
15. Охарактеризуйте транзакционную среду экономической системы.
16. За счет чего открытые экономические системы сохраняют свои индивидуальные особенности?
17. Как (в каких шкалах) измеряются эмерджентные свойства сис-тем?
18. Назовите необходимое условие существования эмерджентного свойства системы.
19. В чем заключается сущность свойства целеустремленности. Как это свойство проявляется в экономических системах?
20. Приведите примеры реактивных, ответных, самонастраиваемых и активных экономических систем.
21. В чем заключается сущность свойства иерархичности экономических систем?
22. Эквивалентны ли понятия «уровень иерархии» и «страта»?
23. В чем заключается сущность свойства многомерности экономической системы?
24. Дайте системное определение понятию «компромисс».
25. Приведите практические примеры использования свойства многомерности при исследовании экономических систем.
26. В чем заключается сущность свойства множественности экономической системы?
27. Приведите примеры множественности функций экономической системы.
28. Как проявляется множественность структуры экономической системы?
29. Приведите примеры эквифинальности и мультифинальности экономических систем.
30. Перечислите причины контринтуитивного поведения экономи-ческих систем.
31. Какой классификационный признак положен в основу первич-ной классификации систем?
32. Назовите основные характеристики естественных систем. При-ведите примеры.
33. Назовите основные характеристики искусственных систем. Приведите примеры.
34. В чем заключается специфика социокультурных систем?
35. К какому классу первичных систем относятся экономические системы?
36. В какой мере естественные, технические и гуманитарные науки привлекаются к анализу экономических систем?
37. Разместите факторы в порядке убывания влияния на конфигурацию системы: внешняя среда, внутренние связи системы, связи системы с внешней средой, элементы системы.
38. Поясните, каким образом моральные ценности лица, принимающего решения, материализуются в реальной экономической системе.
39. Что представляет собой среда, в которой существуют и функционируют экономические системы?
40. Дайте определение экономической системы.
41. Какие классификационные признаки положены в основу пространственно-временной классификации экономических систем?
Date: 2015-07-25; view: 1589; Нарушение авторских прав