Задания. Вычислить интеграл, построив квадратурную формулу интерполяционного типа по заданным узлам

Вычислить интеграл, построив квадратурную формулу интерполяционного типа по заданным узлам. Коэффициенты квадратурной формулы, которые сами являются интегралами от полиномов, вычислить интегрированием по заданной квадратурной формуле с равноотстоящими

узлами (формулы прямоугольников, трапеций, Симпсона) из предыдущей работы. Ответ проверить, вычислив точное значение интеграла.

Вариант 1

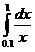, узлы: 0.1, 0.14, 0.2, 0.4, 0.6, 0.7, 0.9, 1;

Вариант 2

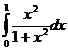, узлы: 0, 0.2, 0.3, 0.5, 0.8, 0.9, 1;

Вариант 3

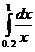, сетка равномерная с шагом 1/5;

Вариант 4

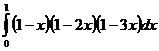, узлы: 0, 1/5, 1/4, 1/3, 1/2, 1;

Вариант 5

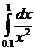, узлы: 0.1, 0.2, 0.3, 0.5, 0.79, 0.884, 1;

Вариант 6

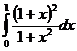, узлы: 0, 0.3, 0.4, 0.5, 0.8, 1;

Вариант 7

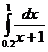, сетка равномерная с шагом 1/5;

Вычислить интегралы по формулам типа Гаусса, пользуясь таблицей узлов и коэффициентов, и оценить погрешности по формуле для погрешности (7.2). Вычислить точное значение интеграла и сравнить ответ.

Вариант 8

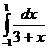, n=4.

Вариант 9

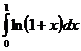, n=5.

Вариант 10

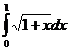, n=3.

Вариант 11

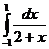, n=5.

Вариант 12

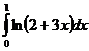, n=4.

Вариант 13

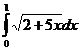, n=4.

Вычислить интегралы по формулам типа Гаусса, пользуясь таблицей узлов и коэффициентов. Контроль вычислений провести применением других квадратурных формул при большом числе узлов (n=100).

Вариант 14

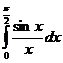, n=11.

Вариант 15

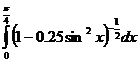, n=3.

Вариант 16

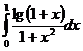, n=4.

Вариант 17

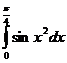, n=9.

Вариант 18

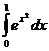, n=9.

Вариант 19

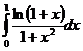, n=3.

Вычислить интегралы по формуле Эрмита (7.5) при небольшом числе узлов (n=4,5,6,7). Вычислить точное значение интеграла и сравнить ответ.

Вариант 20

.

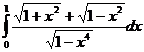Вариант 21

.

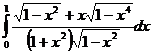Вариант 22

.

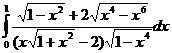Вариант 23

.

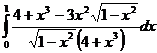Вариант 24

.

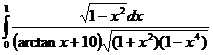Вариант 25

.

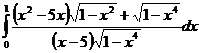Date: 2015-07-22; view: 436; Нарушение авторских прав