Некоторые квадратурные формулы Гаусса

Квадратурная формула Гаусса

(7.1)

Имеет своими узлами корни многочлена Лежандра. Узлы и коэффициенты этой формулы для 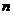от 0 до 15 приведены в табл. 1.

Табл. 1

	Узлы	Коэффициенты		Узлы	Коэффициенты
n=0	0.0		n=11	0.1252334085	0.2491470458
n=1	0.5773502692		0.3678314989	0.2334925365
n=2	0.7745966692	5/9	0.5873179542	0.2031674267
0.0	8/9	0.7699026741	0.1600783285
n=3	0.8611363116	0.3478548451	0.9041172563	0.1069393259
0.3399810436	0.6521451549	0.9815606342	0.0471753363
n=4	0.9061798459	0.2369268851	n=12	0.2304583159	0.2262831802
0.5384693101	0.4786286705	0.4484927510	0.2078160475
0.0	0.5688888899	0.6423493394	0.1781459807
n=5	0.9324695142	0.1713244924	0.8015780907	0.1388735102
0.6612093865	0.3607615730	0.9175983992	0.0921214998
0.2386191861	0.4679139346	0.9841830547	0.0404840047
n=6	0.4058451513	0.3818300505	0.0	0.2325515532
0.7415311855	0.2797053914	n=13	0.1080549487	0.2152638534
0.9491079123	0.1294849661	0.3191123689	0.2051984637
0.0	0.4179591836	0.5152486363	0.1855383974
n=7	0.1834346424	0.3626837833	0.6872929048	0.1572031671
0.5255324099	0.3137066458	0.8272013150	0.2115185706
0.7966664774	0.2223810344	0.9284348836	0.0801580871
0.9602898564	0.1012285362	0.9862838086	0.0351194603
n=8	0.3242534234	0.3123470770	n=14	0.2011940939	0.1984314853
0.6133714327	0.2606106964	0.3941513470	0.1861610000
0.8360311073	0.1806481606	0.5709721726	0.1662692058
0.9681602395	0.0812743883	0.7244177313	0.1395706779
0.0	0.3302393550	0.8482065834	0.1071592204
n=9	0.1488743389	0.2955242247	0.9372733924	0.0703660474
0.4333953941	0.2692667193	0.9879925180	0.0307532419
0.6794095682	0.2190863625	0.0	0.2025782419
0.8650633666	0.1494513491	n=15	0.0950125098	0.1894506104
0.9739065285	0.0666713443	0.2816035507	0.1826034150
n=10	0.2695431559	0.2628045445	0.4580167776	0.1691565193
0.5190961292	0.2331937645	0.6178762444	0.1495959888
0.7301520055	0.1862902109	0.7554044083	0.1246289712
0.8870625997	0.1255803694	0.8656312023	0.0951585116
0.		0.9445750230	0.0622535239
0.0		0.9894009349	0.1255803694

Погрешность квадратурной формулы (7.1) оценивается следующим образом:

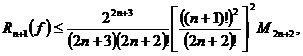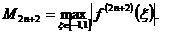где (7.2)

При вычислении интеграла 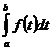следует сделать замену переменной интегрирования 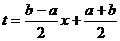, (7.3)

которая превращает отрезок 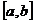в отрезок .

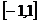Тогда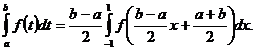

Применяя к интегралу в правой части формулу (7.1), находим

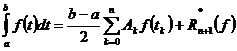, (7.4)

где 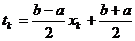; 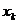– узлы квадратурной формулы Гаусса для отрезка 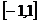и 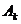– соответствующие им коэффициенты. Остаток квадратуры (7.4)

.

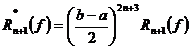Формулами Эрмита называют формулы Гаусса

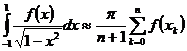, (7.5)

узлами которых являются корни многочлена Чебышева степени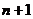

.

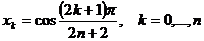Остаточный член квадратурной формулы (7.5) равен

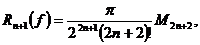где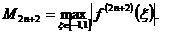

Date: 2015-07-22; view: 323; Нарушение авторских прав