
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Пример1. Вычислить интеграл (узлы: 1, 1.2, 1.4, 1.6, 1.8, 2), построив квадратурную формулу интерполяционного типа по заданным узлам
|
|
Вычислить интеграл 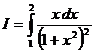 (узлы: 1, 1.2, 1.4, 1.6, 1.8, 2), построив квадратурную формулу интерполяционного типа по заданным узлам. Коэффициенты квадратурной формулы, которые сами являются интегралами от полиномов, вычислить интегрированием по квадратурной формуле прямоугольников с равноотстоящими узлами из предыдущей работы. Ответ проверить, вычислив точное значение интеграла.
(узлы: 1, 1.2, 1.4, 1.6, 1.8, 2), построив квадратурную формулу интерполяционного типа по заданным узлам. Коэффициенты квадратурной формулы, которые сами являются интегралами от полиномов, вычислить интегрированием по квадратурной формуле прямоугольников с равноотстоящими узлами из предыдущей работы. Ответ проверить, вычислив точное значение интеграла.
Решение.
Точное значение интеграла:
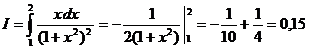 .
.
Для приближенного вычисления интеграла 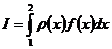 , где
, где 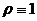 ,
, 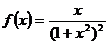 , построим квадратурную формулу вида
, построим квадратурную формулу вида 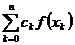 , заменяя
, заменяя 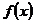 на всем отрезке интерполяционным многочленом степени
на всем отрезке интерполяционным многочленом степени 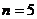 , построенным по узлам интерполирования
, построенным по узлам интерполирования 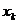 ,
,  (из условия). Обозначим
(из условия). Обозначим 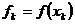 – значения функций в заданных узлах
– значения функций в заданных узлах 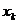 .
.
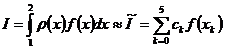 , (1)
, (1)
где 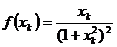 ,
,  .
.
Значения функции 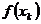 в заданных узлах
в заданных узлах 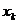 представлены в табл. 2.
представлены в табл. 2.
Табл. 2
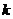
| ||||||
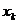
| 1.2 | 1.4 | 1.6 | 1.8 | ||

| 0.25 | 0.2015587208 | 0.1597881665 | 0.1262466860 | 0.1001245995 | 0.08 |
Коэффициенты 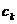 квадратурной формулы вычисляются по формулам
квадратурной формулы вычисляются по формулам
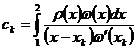 ,
,  , (2)
, (2)
где
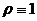 ,
, 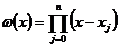 ,
, 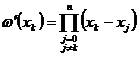 ,
, 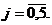
Для решения интеграла (2) введем сетку, разделяющую отрезок 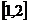 на
на 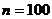 частей, при этом
частей, при этом 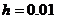 . Выберем на каждом сегменте
. Выберем на каждом сегменте 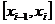 ,
, 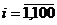 срединную точку
срединную точку 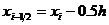 и обозначим
и обозначим 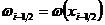 ,
, 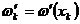 . Применяя квадратурную формулу прямоугольников, получаем:
. Применяя квадратурную формулу прямоугольников, получаем:
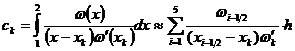 ,
,  .
.
Найдем коэффициенты 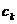 :
:
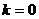 :
: 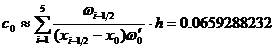 , где
, где 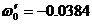 .
.
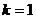 :
: 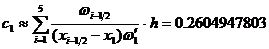 , где
, где 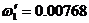 .
.
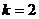 :
: 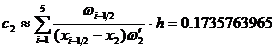 , где
, где 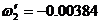 .
.
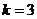 :
: 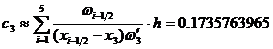 , где
, где 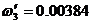 .
.
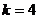 :
: 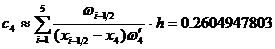 , где
, где 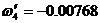 .
.
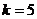 :
: 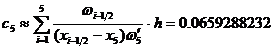 , где
, где 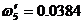 .
.
Подставляя найденные нами значения  (табл. 2) и
(табл. 2) и 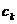 (
( ) в квадратурную формулу (1), найдем приближенное значение интеграла:
) в квадратурную формулу (1), найдем приближенное значение интеграла:
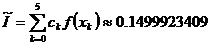 .
.
Сравним точное значение интеграла с приближенным:
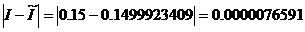 .
.
Date: 2015-07-22; view: 348; Нарушение авторских прав