
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Решение задач линейного программирования симплекс-методом
|
|
Если условия задачи линейного программирования не противоречивы, то область ее допустимых решений образует выпуклый многогранник в n-мерном пространстве (многоугольник для двух переменных). При этом оптимальное решение, если оно существует, обязательно достигается в некоторой вершине многогранника (возможно, и более чем в одной).
Таким образом, чтобы найти решение задачи линейного программирования, достаточно перебрать лишь планы, соответствующие вершинам многогранника допустимых решений. Такие планы называют опорными. Однако в сложных задачах и число вершин может оказаться чрезмерно большим, вследствие чего нахождение всех опорных планов потребует огромного объема вычислений.
Симплекс-метод позволяет осуществить упорядоченный, направленный перебор вершин многогранника. После определения одной из вершин этот метод помогает установить, является ли найденный план оптимальным, то есть достигнут ли в этой вершине максимум целевой функции. Если план неоптимален, то производится переход к такой соседней вершине многогранника, которая обеспечивает большее (или в крайнем случае равное предыдущему) значение целевой функции. Симплекс-метод называют еще методом последовательного улучшения плана. Повторное применение указанной процедуры приводит за конечное число шагов к вершине, соответствующей оптимальному плану.
Симплекс-метод применяется к задаче, записанной в канонической форме (используем одну из двойственных задач линейного программирования):
f(x) = 10Х1 + 14Х2 + 12Х3 + 0×Х4 + 0×Х5 + 0×Х6 ® max,
4X1 + 2X2 + X3 + X4 = 180,
3X1 + X2 + 3X3 + X5 = 210,
X1 + 2X2 + 5X3 + X6 = 244.
Для решения задачи линейного программирования составим симплексную таблицу
| Базис Б | Коэффициенты функции цели Сi | План Х | Коэффициенты функции цели Сi | q = (Хi / 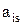 )min )min
| |||||
| Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | ||||
    Х2®Х4 Х2®Х4
| 180/2 = 90 min | ||||||||
| Х5 | 210/1 =210 | ||||||||
| Х6 | 244/2 =122 | ||||||||
f(x) = 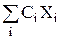 = 0 = 0
| -10 | -14 | -12 | ключевая строка | |||||
| Значение целевой функции при данном опорном плане | min Ключевой столбец | ||||||||
Оценки переменных Dj = 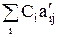 - Cj - Cj
|
В первом столбце вписаны базисные неизвестные, второй содержит коэффициенты при базисных неизвестных в целевой функции, в третьем – правые части уравнений системы ограничений. Далее записана матрица из коэффициентов левой части системы ограничений (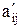 ). В верхней строке над неизвестными записаны соответствующие им коэффициенты в целевой функции. В последней строке записывается значение целевой функции при данном опорном плане, которое вычисляется по формуле f(x) =
). В верхней строке над неизвестными записаны соответствующие им коэффициенты в целевой функции. В последней строке записывается значение целевой функции при данном опорном плане, которое вычисляется по формуле f(x) = 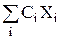 , и далее – оценки неизвестных, найденные по формуле Dj =
, и далее – оценки неизвестных, найденные по формуле Dj = 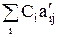 - Cj. Если среди оценок Dj есть отрицательные, то опорный план не является оптимальным и значение целевой функции можно улучшить. Для этого нужно пересчитать симплексную таблицу, выбрав соответствующим образом ключевой элемент, стоящий на пересечении ключевой строки и ключевого столбца, причем берется столбец с наибольшей по абсолютной величине отрицательной оценкой.
- Cj. Если среди оценок Dj есть отрицательные, то опорный план не является оптимальным и значение целевой функции можно улучшить. Для этого нужно пересчитать симплексную таблицу, выбрав соответствующим образом ключевой элемент, стоящий на пересечении ключевой строки и ключевого столбца, причем берется столбец с наибольшей по абсолютной величине отрицательной оценкой.
Для определения ключевой строки находим отношения правых частей уравнений к положительным элементам ключевого столбца. Полученные значения q записываются в последний столбец симплексной таблицы. Из них выбирается наименьшая величина, которая указывает на ключевую строку.
Пересчет таблицы производится по следующему правилу: элементы ключевой строки делятся на ключевой элемент. Далее, с помощью метода Жордана Гаусса проводят пересчет таблицы таким образом, чтобы элементы ключевого столбца имели единицу на месте ключевого элемента и нули на месте всех остальных элементов. Для этого вычтем из элементов третьей строки соответствующие элементы первой строки, а из элементов второй строки – элементы первой строки, поделенные на два (на ключевой элемент).
Переменная, соответствующая ключевой строке, выводится из базиса, а переменная, соответствующая ключевому столбцу, вводится вместо нее в базис.
Для каждого шага итерации строится своя симплексная таблица:
| Б | Сi | Х | q | ||||||
| Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | ||||
 Х2 Х2
| 1/2 | 1/2 | 90: 1/2 = 180 | ||||||
| Х5 | 5/2 | -1/2 | 120: 5/2 = 48 | ||||||
  Х3®Х6 Х3®Х6
| -3 | -1 | 64: 4 = 16 min | ||||||
| f(x) = 1260 | -5 | ||||||||
| Отрицательная оценка |
Поскольку среди оценок неизвестных есть отрицательная, необходимо продолжить расчеты и составить новую таблицу. Для этого элементы третьей (ключевой) строки разделим на ключевой элемент. Умножив новые элементы третьей строки на 1/2, вычтем их из соответствующих элементов первой строки предыдущей таблицы. Затем, умножив новые элементы третьей строки на 5/2, вычтем их из соответствующих элементов второй строки предыдущей таблицы. Третья симплексная таблица имеет вид
| Б | Сi | Х | q | ||||||
| Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | ||||
| Х2 | 19/8 | 5/8 | -1/8 | ||||||
| Х5 | 23/8 | 1/8 | -5/8 | ||||||
| Х3 | -3/4 | -1/4 | 1/4 | ||||||
 f(x) = 1340 f(x) = 1340
| 57/4 | 23/4 | 5/4 | ||||||
| Двойственные оценки сырья |
Поскольку среди оценок нет отрицательных, то это значит, что найдено оптимальное решение. Из таблицы видно, что при оптимальном плане следует выпускать изделий вида В в количестве 82 штук, изделий С – 16 штук. При этом остаются неиспользованными 80 кг сырья второго вида, а общий доход от продажи изделий составит 1340 ден.ед. Из таблицы также видно, что оптимальным решением двойственной задачи является Y* = (23/4, 0, 5/4), поскольку решение двойственной задачи находится в столбцах, соответствующих дополнительным переменным исходной задачи (Х4, Х5, Х6).
Переменные 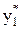 и
и 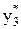 обозначают условные двойственные оценки единицы сырья первого и третьего вида. Они отличны от нуля, и сырье этих видов полностью использовано при оптимальном плане производства. Переменная
обозначают условные двойственные оценки единицы сырья первого и третьего вида. Они отличны от нуля, и сырье этих видов полностью использовано при оптимальном плане производства. Переменная 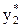 = 0, и второй вид сырья полностью не используется.
= 0, и второй вид сырья полностью не используется.
Таким образом, положительную двойственную оценку имеют те виды сырья, которые используются полностью, а значит, они характеризуют дефицитность сырья: чем больше двойственные оценки, тем дефицитнее сырье. Более того, двойственные оценки показывают, насколько возрастет оптимальное (максимальное) значение функции цели прямой задачи при увеличении количества сырья соответствующего вида на 1 кг. Так, увеличение количества сырья первого вида на 1 кг приведет к новому оптимальному плану производства изделий, при котором доход возрастет на 23/4 = 5,75 и станет равным 1345,75 ден.ед. При этом числа, стоящие в столбце Х4 последней симплексной таблицы, покажут, что это может быть достигнуто за счет увеличения выпуска изделий В на 5/8 единиц и выпуска изделий С на 1/4 единицы. Использование сырья второго вида уменьшится при этом на 1/8 кг.
Также увеличение на 1 кг сырья третьего вида дает новый оптимальный план, при котором доход возрастет на 5/4 = 1,25 ден.ед. и составит 1341,25 ден.ед. Это будет достигнуто за счет увеличения выпуска изделия С на 1/4 единицы и уменьшения выпуска изделия В на 1/8 единицы, причем объем используемого сырья второго вида возрастет на 5/8 кг.
Вычислим минимальное значение целевой функции двойственной задачи:
F(y) = 180 × 23/4 + 210 × 0 + 244 × 5/4 = 1340,
оно совпадает с максимальным значением целевой функции исходной задачи.
Если подставить двойственные оценки оптимального плана в систему ограничений двойственной задачи, то получим
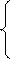 23 + 5/4 > 10,
23 + 5/4 > 10,
23/2 + 5/2 = 14,
23/4 + 25/4 = 12.
Когда ограничение выполнено как строгое неравенство, то двойственная оценка сырья на производство одного изделия А выше дохода от реализации одного изделия, значит, данный вид изделий выпускать невыгодно. Если как равенство, то выпускать такие изделия экономически целесообразно.
Тема 5. Транспортная задача
Математическая постановка задачи состоит в определении оптимального плана перевозок некоторого груза из m пунктов отправления A1, A2, …, Am в n пунктов назначения B1, B2, …, Bn. При этом в качестве критерия оптимальности обычно выбирается либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки.
Обозначим через Cij стоимость перевозки единицы груза из i–го пункта отправления в j–й пункт назначения; аi - запасы груза в i–м пункте отправления (величина предложения); bj - потребности в этом грузе в j–м пункте назначения (величина спроса); Xij - объем перевозок (количество перемещаемых единиц груза) из i–го пункта отправления в j–й пункт назначения.
Тогда математическая модель транспортной задачи имеет следующий вид: определить минимум целевой функции
f(x) = 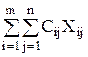 ® min (1)
® min (1)
при выполнении следующих ограничений:
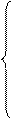
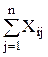 = аi; i =
= аi; i = 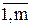 , (2)
, (2)
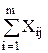 = bj; j =
= bj; j = 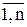 , (3)
, (3)
Хij ³ 0; i = 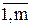 ; j =
; j = 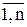 . (4)
. (4)
Обычно исходные данные транспортной задачи представляются в виде таблицы. Внутренняя часть этой таблицы является объединением двух матриц: матрицы перевозок Х = { Xij } и матрицы стоимостей С = { Сij }.
| Пункты отправления | Пункты назначения | Запасы (предложение) | |||||
| В1 | В2 | … | Вj | … | Вn | ||
 А1 А1
| С11 Х11 | С12 Х12 | … | C1j Х1j | … | C1n Х1n | а1 |
| А2 | С21 Х21 | С22 Х22 | … | C2j Х2j | … | C2n Х2n | а2 |
| … | … | … | … | … | … | … | … |
| Аi | Сi1 Хi1 | Сi2 Хi2 | … | Сij Хij | … | Сin Хin | аi |
| … | … | … | … | … | … | … | … |
| Аm | Сm1 Хm1 | Сm2 Хm2 | … | Сmj Хmj | … | Сmn Хmn | аm |
| Потребности (спрос) | b1 | b2 | … | bj | … | bm | Sbj = Sаi |
Если общий запас груза у поставщиков равен потребности в грузе у потребителей, т.е. если выполняется условие
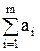 =
= 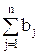 , (5)
, (5)
то модель такой транспортной задачи называется закрытой, а если условие не выполняется, то задача называется открытой.
Определение 1. Всякое неотрицательное решение систем линейных уравнений (2) и (3), определяемое матрицей Х = { Xij }; i = 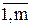 ; j =
; j = 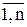 , называется планом транспортной задачи.
, называется планом транспортной задачи.
Определение 2. План Х* = {Xij*}, при котором функция цели 1 принимает минимальное значение, называется оптимальным планом транспортной задачи.
Ограничения 2 и 3 транспортной задачи представляют собой две группы уравнений. Первая из них, т.е. система уравнений 2, означает то, что сумма перевозок по каждой строке таблицы должна быть равна соответствующему запасу аi. Каждое уравнение второй системы 3 означает то, что сумма перевозок по каждому столбцу таблицы должна быть равна соответствующей потребности bj. Транспортная задача представляет собой задачу линейного программирования, записанную в каноническом виде. Следовательно, ее можно решать симплексным методом. Однако для решения транспортных задач существуют специальные методы.
Особенности транспортной задачи:
1. Закрытая транспортная задача всегда совместна, обладает планом, т.е. имеет решение.
2. Если значения и аi-е и bj-е – целые и неотрицательные, то транспортная задача имеет целочисленное решение.
3. Клетки таблицы транспортной задачи с координатами, в которых проставлены значения перевозок, называются базисными и соответствуют базисным переменным, а остальные клетки остаются свободными. Для невыраженного опорного плана в таблице транспортной задачи будет заполнена положительными числами m + n – 1 клетка. Если же опорный план задачи вырожден, то часть базисных клеток будет заполнена нулями.
Нахождение первоначального плана
Для определения первоначального опорного плана существуют несколько различных методов. Это – метод северо-западного угла, метод минимального элемента, или минимальной стоимости, и другие.
Метод северо-западного угла. Пусть условие транспортной задачи задано в следующей таблице:
| Пункты отправления | Пункты назначения | Предложение | |||
| В1 | В2 | В3 | В4 | ||
| А1 | 5 | 4 | 2 | 5 | |
| А2 | 6 | 1 | 1 | 3 | |
| А3 | 2 | 3 | 1 | 8 | |
| А4 | 6 | 3 | 2 | 1 | |
| Спрос | S250 |
Поскольку сумма запасов (предложения) равна сумме потребностей (спроса) – имеем задачу закрытого типа.
Матрицу перевозок начинаем заполнять с левого верхнего (северо-западного) угла, с клетки (1,1). Для этого сравниваем два значения а1 = 30 и b1= 20, т.е. попытаемся удовлетворить потребность первого пункта назначения за счет запасов первого пункта отправления. Запасы пункта А1 больше потребности пункта В1, следовательно, в качестве значения Х11 выбираем меньшее число – b1 и запишем это число в соответствующей клетке таблицы. Таким образом, потребность пункта В1 в грузе удовлетворена, и поэтому все остальные числа этого столбца (Х21, Х31, Х41) считаем равными нулю, а соответствующие им клетки оставляем свободными.
Получаем новую матрицу из трех столбцов (В2, В3, В4) и четырех строк (А1, А2, А3, А4) и новое значение запаса у первого пункта отправления (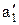 = 30 – 20 = 10). Далее сравниваем значения
= 30 – 20 = 10). Далее сравниваем значения 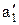 = 10 и b2 = 90 и повторяем алгоритм. Меньшее из этих значений, равное 10, выбираем в качестве Х12 и записываем в клетку (1,2) таблицы. Тогда запас пункта А1 будет полностью исчерпан, следовательно, остальные значения перевозок из первой строки (Х13, Х14) принимаем равными нулю, а соответствующие клетки остаются свободными. Продолжая заполнять таблицу, таким образом дойдем до клетки (4,4). Построенный план является опорным. В рассматриваемой задаче число пунктов отправления m = 4 и число пунктов назначения n = 4, следовательно, невырожденный план задачи определяется числами, стоящими в m+n–1 = 4 + 4 – 1 = 7 заполненных клетках.
= 10 и b2 = 90 и повторяем алгоритм. Меньшее из этих значений, равное 10, выбираем в качестве Х12 и записываем в клетку (1,2) таблицы. Тогда запас пункта А1 будет полностью исчерпан, следовательно, остальные значения перевозок из первой строки (Х13, Х14) принимаем равными нулю, а соответствующие клетки остаются свободными. Продолжая заполнять таблицу, таким образом дойдем до клетки (4,4). Построенный план является опорным. В рассматриваемой задаче число пунктов отправления m = 4 и число пунктов назначения n = 4, следовательно, невырожденный план задачи определяется числами, стоящими в m+n–1 = 4 + 4 – 1 = 7 заполненных клетках.
| Пункты отправления | Пункты назначения | Предложение | |||
| В1 | В2 | В3 | В4 | ||
| А1 | 20 5 | 10 4 | 2 | 5 | |
| А2 | 6 | 70 1 | 1 | 3 | |
| А3 | 2 | 10 3 | 40 1 | 8 | |
| А4 | 6 | 3 | 30 2 | 70 1 | |
| Спрос | - |
Запишем первоначальный опорный план в виде матрицы Х:
Х = 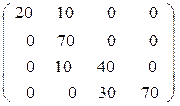 .
.
Согласно данному плану перевозок функция цели – общая стоимость перевозок всего груза - составляет
f(х) = 5 × 20 + 4 × 10 + 1 × 70 + 3 × 10 + 1 × 40 + 2 × 30 + 1 × 70 = 410.
Вырожденный план. При построении опорного плана нужно следить, чтобы сумма перевозок по каждой строке была равна соответствующим запасам, а сумма перевозок по каждому столбцу – потребности. Количество заполненных клеток равно m + n – 1. Если план вырожденный, т.е. если на очередном шаге запас аi равен потребности bj, в этом случае необходимо считать одну из клеток (либо справа, либо под последней заполненной клеткой) базисной со значением, равным нулю. Этот нуль вписывают, и соответствующая клетка считается занятой.
Пусть условия задачи заданы следующей таблицей:
| Пункты отправления | Пункты назначения | Предложение | |||
| В1 | В2 | В3 | В4 | ||
| А1 | 20 5 | 10 4 | 2 | 5 | |
| А2 | 6 | 70 1 | 1 | 3 | |
| А3 | 2 | 0 3 | 30 1 | 20 8 | |
| А4 | 6 | 3 | 2 | 100 1 | |
| Спрос | S250 |
На первом шаге заполняем северо-западный угол, полагая Х11 = 20, клетки (2,1), (3,1) и (4,1) остаются свободными. На втором шаге полагаем Х12 = 10. Этим мы используем полностью запас пункта А1. Остальные клетки первой строки (1,3) и (1,4) остаются свободными. На третьем шаге рассматриваем перевозку Х22. Поскольку в этом случае запас пункта А2, равный 70, совпадает с оставшейся неудовлетворенной потребностью пункта В2, равной 70, то выбираем Х22 = 70. Этим самым заполняется одновременно и вся вторая строка и весь второй столбец. В этом случае нужно считать одну из переменный Х23 или Х32 базисной со значением, равным нулю. Пусть Х32 = 0. Проставив в соответствующей клетке базисный нуль, мы получаем при продолжении процесса заполнения таблицы m + n – 1 заполненную клетку. Если не проставить нулевую базисную переменную, окажется, что число занятых положительными перевозками клеток меньше, чем m + n – 1.
Метод минимального элемента. Выбор пунктов отправления и назначения можно производить иначе, ориентируясь на стоимость перевозок, т.е. на каждом шаге следует выбирать какую-нибудь клетку, отвечающую минимальной стоимости перевозки. Если таких клеток несколько, то можно выбрать любую.
Этот метод позволяет найти первоначальный опорный план с меньшей стоимостью перевозок, чем план, полученный методом северо-западного угла:
| Пункты отправления | Пункты назначения | Предложение | |||
| В1 | В2 | В3 | В4 | ||
| А1 | 10 5 | 4 | 20 2 | 5 | |
| А2 | 6 | 70 1 | 1 | 3 | |
| А3 | 2 | 3 | 50 1 | 8 | |
| А4 | 10 6 | 20 3 | 2 | 70 1 | |
| Спрос | - |
Порядок заполнения таблицы: находим клетки с наименьшим значением стоимости перевозки и рассмотрим величину потребности и запаса для соответствующих пунктов. Заполним клетки (2,2), (3,3), (4,4) и подсчитаем остатки неизрасходованных запасов и величины неудовлетворенной потребности. Так, запасы пункта А2 полностью расходуются на удовлетворение потребности пункта В2, поэтому при нахождении первоначального опорного плана клетки второй строки, кроме (2,2), должны остаться свободными. Потребности пункта В2 остаются неудовлетворенными на 20 единиц груза, поэтому клетки второго столбца, кроме (2,2), могут быть заполнены перевозками. Аналогично рассматриваем заполнение клеток (3,3) и (4,4). Найдем свободные клетки с наименьшими стоимостями перевозок, которые могут быть заполнены, это, например, клетка (1,3) или (4,3). Заполним клетку (1,3) и подсчитаем остаток. Затем заполним клетку (4,2), на следующем шаге клетку (1,1) и, наконец, (4,1).
Значение функции цели для первоначального опорного плана
f(х) = 10 × 5 + 20 × 2 + 70 × 1 + 50 × 1 + 10 × 6 + 20 × 3 + 70 × 1 = 400.
Date: 2015-07-24; view: 539; Нарушение авторских прав