
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Тема 4. Модели линейного программирования
|
|
Раздел математических методов, в котором рассматриваются способы решения задач на нахождение экстремума функции цели при ограничении области допустимых значений в форме уравнений или неравенств, называется математическим программированием. Другими словами, математическое (оптимальное) программирование рассматривает задачи планирования, распределения ограниченных ресурсов наилучшим образом, для достижения поставленных целей.
Общая задача математического программирования имеет вид
Определить экстремум функции
f(x) ® extremum (max, min)
при выполнении условий
gi(x) = (³, £)bi, (i = 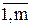 ),
),
x = (x1, x2,… xj …xn), xj ³ 0, (j = 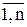 ),
),
где f(x) – целевая функция;
gi(x) - функция ограничения;
bi - действительное число, константа ограничения.
Если функции f(x) и gi(x) представлены в виде линейных функций, то оптимизационная задача называется задачей линейного программирования.
Таким образом, линейное программирование – это область математического программирования, посвященная теории и методам решения задач нахождения условного экстремума и характеризующаяся линейной зависимостью между переменными.
Примеры задач линейного программирования
1. Задача планирования производства
Date: 2015-07-24; view: 386; Нарушение авторских прав