
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Массового обслуживания
|
|
Чтобы улучшить работу СМО путем изменения ее организации, необходимо рассчитать показатели качества ее функционирования при существующем варианте организации и при других возможных вариантах и на основе этих расчетов принять решение.
А. Система обслуживания с потерями
Вероятность того, что в обслуживающей системе находится точно k требований, т.е. занято k обслуживающих аппаратов:
Рk = 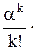 Р0 , (8)
Р0 , (8)
где k – число требований в системе (k = 1, 2, 3, …, n);
n – число обслуживающих аппаратов;
Р0 – вероятность того, что в системе нет ни одного требования.
Вероятность того, что все обслуживающие аппараты свободны:
Р0 = ( )-1 . (9)
)-1 . (9)
Вероятность отказа в обслуживании. Отказ происходит в случае, когда все обслуживающие аппараты заняты. Тогда вероятность отказа равна вероятности того, что все аппараты заняты, или вероятность того, что в системе находится ровно n требований:
Ротказа = 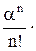 (
( )-1 . (10)
)-1 . (10)
Степень загрузки системы характеризуется средним числом занятых обслуживающих аппаратов
М = 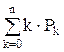 . (11)
. (11)
Пример. В механическом цехе на одном участке работают 3 контролера. Если деталь поступает в ОТК, когда контролеры заняты, она уходит на склад готовой продукции, не ожидая контроля. Известно, что среднее число деталей, поступающих в ОТК в течение 1 ч. равно 24, а среднее время обслуживания равно 5 мин. Какова вероятность того, что загружены контролеры работой
Решение. n = 3, l = 24, 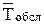 = 5 мин =
= 5 мин = 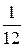 ч., n =
ч., n = 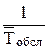 = 12,
= 12,
a = 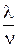 =
= 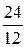 = 2, n ³ a.
= 2, n ³ a.
Ротказа = 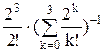 =
= 
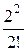 +
+ 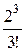 )-1 =
)-1 = 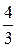 × (1+ 2 + 2 +
× (1+ 2 + 2 + 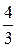 )-1 =
)-1 =
= 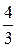 × (
× (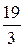 )-1 =
)-1 = 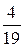 = 0,21.
= 0,21.
Вероятность отказа 0,21 означает, что из 100 деталей в среднем ОТК пройдет 79 деталей и не пройдет 21 деталь.
Определим степень загрузки контролеров
М = 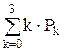 = 0 × Р0 + 1 × Р1 + 2 × Р2 + 3 × Р3.
= 0 × Р0 + 1 × Р1 + 2 × Р2 + 3 × Р3.
Расчеты представлены в следующей таблице:
| Число занятых контролеров | 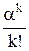
| Рk = 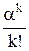 × Р0 × Р0
| k × Рk |
| 0,16 | |||
| 0,32 | 0,32 | ||
| 0,32 | 0,64 | ||
| 4/3 | 0,21 | 0,63 | |
| S | 19/3 | » 1 | 1,59 |
Р0 = (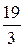 )-1 = 0,16;
)-1 = 0,16;
М = 1,59 означает, что полностью занято более полутора контролеров.
Коэффициент загрузки одного контролера
Кзаг = 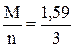 = 0,53,
= 0,53,
т.е. каждый контролер в среднем занят более половины дня.
Б. Система обслуживания с ожиданием или без потерь
(замкнутая система массового обслуживания)
Вероятность того, что в системе занято k обслуживающих аппаратов при условии, что число требований, находящихся в системе, не превосходит числа обслуживающих аппаратов, т.е. когда очереди нет:
Рk = 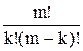 × ak × Р0, (12)
× ak × Р0, (12)
где k– число требований (0 £ k £ n);
n – число обслуживающих аппаратов;
m – наибольшее возможное число требований, находящихся в обслуживаемой системе одновременно.
Вероятность того, что в системе находится k требований для случая, когда их число больше числа обслуживающих аппаратов, т.е. когда есть очередь:
Рk = 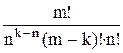 ×ak × Р0, (13)
×ak × Р0, (13)
где (n £ k £ m).
Вероятность того, что все обслуживающие аппараты свободны:
Р0 = (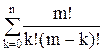 ×ak +
×ak + 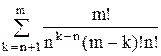 × ak)-1. (14)
× ak)-1. (14)
Введем обозначения для краткой записи (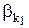 ) и (
) и (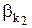 ), тогда
), тогда
Р0 = 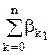 +
+ 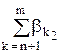 . (15)
. (15)
Среднее число требований, ожидающих начала обслуживания, т.е. средняя длина очереди
М1 = 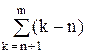 × Рk. (16)
× Рk. (16)
Коэффициент простоя обслуживаемого требования в ожидании обслуживания
К1 = 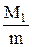 . (17)
. (17)
Среднее число требований, находящихся в обслуживающей системе, т.е. в очереди и в обслуживании
М2 = 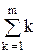 × Рk. (18)
× Рk. (18)
Коэффициент простоя обслуживаемого требования в обслуживающей системе
К2 =  . (19)
. (19)
Среднее число свободных обслуживающих аппаратов
М3 = 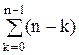 × Рk. (20)
× Рk. (20)
Коэффициент простоя обслуживающего аппарата
К3 =  . (21)
. (21)
Пример. Два рабочих обслуживают группу из 9 станков. В среднем каждый станок останавливается один раз в час. Обслуживание одного станка занимает у рабочего в среднем 6 мин. Определить основные характеристики эффективности функционирования системы массового обслуживания.
Решение. n = 2, m = 9, l = 1, 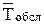 = 6 мин = 0,1 ч., n =
= 6 мин = 0,1 ч., n = 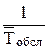 = 10,
= 10,
a = 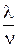 = 0,1.
= 0,1.
В любой момент времени система находится в одном из своих возможных состояний:
k = 0 – все станки работают, очереди нет;
k = 1 – один станок обслуживается, очереди нет;
k = 2 – два станка обслуживаются, очереди нет;
k = 3 – два станка обслуживаются, один в очереди, остальные работают;
………………………..………………………..………………………………
k = 9 – два станка обслуживаются, семь в очереди на обслуживание, т.е. ни один станок не работает.
Этим состояниям системы соответствуют вероятности:
Р0, Р1, Р2, Р3, …, Р9.
Определим значения 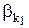 для случая, когда очереди нет (0 £ k £ 2):
для случая, когда очереди нет (0 £ k £ 2):
b0 = 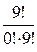 × 0,1° = 1; b1 =
× 0,1° = 1; b1 =  × 0,11 = 0,9; b2 =
× 0,11 = 0,9; b2 =  × 0,12 = 0,36.
× 0,12 = 0,36.
Определим значения 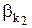 для случая, когда очередь есть (3 £ k £ 9):
для случая, когда очередь есть (3 £ k £ 9):
b3 = 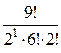 × 0,13 = 0,126; … b9 =
× 0,13 = 0,126; … b9 = 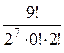 × 0,19 = 0,0000014175.
× 0,19 = 0,0000014175.
Результаты расчетов представлены в таблице:
| Число требований, k | Число требований, ожидающих обслуживания, k - n | Число свободных рабочих, n - k | 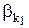 и и 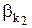
| Рk=bk×Р0 | (k-n) Рk | k×Рk | (n-k) Рk |
| - | 0,4106 | - | - | 0,8212 | |||
| - | 0,9 | 0,3695 | - | 0,3695 | 0,3695 | ||
| - | - | 0,36 | 0,1478 | - | 0,2956 | - | |
| - | 0,126 | 0,0517 | 0,0517 | 0,1551 | - | ||
| - | 0,0378 | 0,0155 | 0,031 | 0,062 | - | ||
| - | 0,00945 | 0,00388 | 0,01164 | 0,0194 | - | ||
| - | 0,00189 | 0,000776 | 0,003104 | 0,004656 | - | ||
| - | 0,0002835 | 0,0001164 | 0,000582 | 0,0008148 | - | ||
| - | 0,0002835 | 0,0000116 | 0,0000696 | 0,0000928 | - | ||
| - | 0,0000014175 | 0,0000005 | 0,0000035 | 0,0000045 | - | ||
| S | - | - | 2,43545 | - | 0,098 | 0,949 | 1,1862 |
Вероятность того, что в системе не будет ни одного требования:
Р0 = (2,43545)-1 = 0,4106.
Среднее число станков, стоящих в очереди:
М1 = 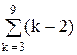 × Рk = 0,098.
× Рk = 0,098.
Это означает, что в среднем из 9 станков 0,098 простаивают в очереди на обслуживание.
Коэффициент простоя станка в очереди
К1 = 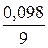 = 0,11.
= 0,11.
Это означает, что в среднем каждый станок 1,1 % времени простаивает в очереди.
Среднее число простаивающих станков (в очереди и обслуживании)
М2 = 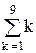 × Рk = 0,949.
× Рk = 0,949.
Это означает, что в среднем 95 % рабочего времени 1 станок из 9 не будет работать.
Коэффициент простоя станка в системе обслуживания
К2 = 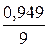 = 0,105.
= 0,105.
Это означает, что 10,5 % времени в среднем будет простаивает каждый станок из 9.
Среднее число свободных обслуживающих аппаратов (рабочих)
М3 = 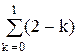 × Рk = 1,1862.
× Рk = 1,1862.
Это означает, что из двух человек в среднем один всегда свободен, а другой свободен в течение 18,6 % времени.
Коэффициент простоя рабочего
К3 = 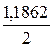 = 0,59.
= 0,59.
Это означает, что в среднем каждый рабочий 59 % рабочего времени простаивает без работы.
Тема 3. Модель межотраслевого баланса
Важнейшим условием нормального развития национального хозяйства является сбалансированность общественного производства на всех уровнях. Эффективным аппаратом для определения сбалансированных пропорций развития являются балансовые модели производства и распределения продукции. Использование балансовых моделей помогает органам государственного управления экономикой способствовать предупреждению возникновения диспропорций в развитии отраслей национальной экономики.
Балансовые модели составляются для экономических систем разных уровней. Например, на уровне национального хозяйства используется модель межотраслевого баланса производства и распределения продукции, а на уровне предприятия – модель межпродуктового баланса.
Суть балансовой модели состоит в том, что затраты должны компенсироваться доходами. Данный метод позволяет для каждой отрасли определить количество продукции, которое она должна выпустить, чтобы удовлетворить потребность всех других отраслей, включая непроизводственную сферу и потребности внешней торговли. Рассмотрим балансовую модель в стоимостном выражении.
Date: 2015-07-24; view: 477; Нарушение авторских прав