
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Расчет временных параметров событий
|
|
Введем обозначения (рис. 10):
i, j – номер события; I - исходное событие; J - завершающее событие;
tPi, tPj - ранний срок свершения события;
tni, tnj - поздний срок свершения события;
Rj, Rj - резерв времени события;
t(LI, j) - продолжительность пути от события I до события j;
tкр- продолжительность критического пути;
tij - продолжительность работы.
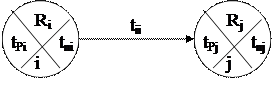 |
Рис. 10. Временные параметры событий
Расчет ранних сроков свершения событий начинается с первого события к последнему (слева направо). Максимальная продолжительность среди путей, ведущих от исходного события до j-го:
tPj = 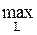 t(LIj). (1)
t(LIj). (1)
Максимальное время завершения всех k работ, входящих в j-е событие:
tPi = 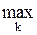 (
( +
+ 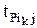 ). (2)
). (2)
Для исходного события ранний срок свершения события tPI = 0, для завершающего события tPJ = tкр.
Расчет поздних сроков свершения событий начинается с последнего события до начального (справа налево). Разность между длительностью критического пути и максимальным из путей, ведущих от i-го события до завершающего:
tni = tкр - 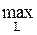 t(LiJ). (3)
t(LiJ). (3)
Минимальная разница между поздними сроками свершения последующих событий для всех k работ, выходящих из i-го события и длительностью этих работ:
tni = 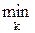 (
(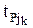 +
+ 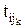 ). (4)
). (4)
Поздний срок свершения завершающего события tnJ = tPJ = tкр.
Резерв времени события показывает, на какой допустимый период времени можно задержать наступление данного события, не увеличивая при этом срок выполнения всего комплекса работ:
Ri = tni - tpi. (5)
События критического пути имеют нулевой резерв времени.
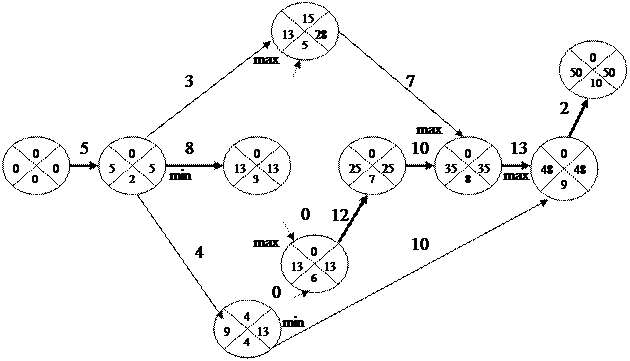
Определим временные параметры событий непосредственно на сетевом графике (рис. 11).
Рис. 11. Расчет временных параметров событий
Расчет ранних сроков свершения событий начинается слева направо, от первого события до десятого. К раннему сроку свершения предшествующего события (левый сектор) прибавляется продолжительность последующей работы, получаем ранний срок свершения последующего события. Если в событие входят несколько работ, то ранний срок его свершения определяется по максимуму, то есть событие не произойдет, пока не завершатся все эти работы.
Расчет поздних сроков свершения событий начинается справа налево, от десятого события к первому. Из позднего срока свершения последующего события (правый сектор) вычитается продолжительность предшествующей работы, получаем поздний срок свершения предшествующего события. Если из предшествующего события входят несколько работ, то поздний срок его свершения определяется по минимуму, то есть из всех возможных значений позднего срока свершения выбирается минимальное.
Результаты расчета представлены в табл. 2.
Таблица 2
| № события | Сроки свершения события | Резерв события (Ri) | |
| tpi | tni | ||
Расчет временных параметров работ
Для иллюстрации расчетов рассмотрим следующее графическое построение (рис. 12).
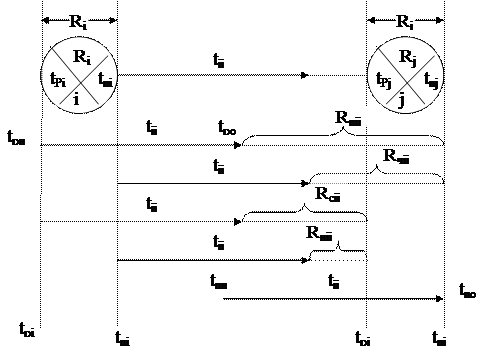
Рис. 12. Временные параметры работ и событий
Поздний срок начала работы tnнij:
tnнij = tnj - tij. (9)
Полный резерв времени работы Rnij показывает, насколько можно увеличить время выполнения данной работы, не изменяя окончательного срока выполнения комплекса работ:
Rnij = tnj - tpi - tij. (10)
Частный резерв времени работы (Rчij) – это часть полного резерва, на которую можно увеличить время завершения работы, уложившись в допустимо поздний срок ее окончания:
Rчij = tnj - tni - tij, (11)
Rчij = tnij - Ri. (12)
Свободный резерв времени работы Rсij – это часть полного резерва, на которую можно увеличить время завершения работы, уложившись в ранний срок свершения ее последующего события:
Rсij = tpj - tpi - tij, (13)
Rсij = tnij - Rj. (14)
Независимый резерв времени работы Rнij – это часть полного резерва, которая используется на увеличение продолжительности только данной работы, при этом все предшествующие работы могут заканчиваться в свои поздние сроки, а все последующие – в ранние:
Rнij = tpj - tni - tij, (15)
Rнij = Rnij - Ri - Rj. (16)
Использование независимого резерва не влияет на величину резерва времени других работ.
Частные случаи при расчете резервов:
1. Если на критическом пути лежит событие i, то из выражения (12) следует
Ri = 0; Rnij = Rчij.
2. Если на критическом пути лежит событие j, то из выражения (14) следует
Rj = 0; Rnij = Rcij.
3. Если на критическом пути лежат и событие i и событие j, но сама работа не принадлежит критическому пути, то для этой работы все резервы равны
Ri = 0; Rj = 0; Rnij = Rчij = Rcij = Rнij.
Коэффициент загруженности работы Кз.
Кз = 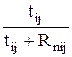 . (17)
. (17)
Результаты расчета временных параметров работ представлены в табл. 3.
Таблица 3
| Код работы i - j | Длительность работы, tij | Сроки работы | Резервы времени | Коэффициент загруженности, Кз | ||||||
| tрн | tро | tnн | tno | Rn | Rч | Rс | Rн | |||
| 1 – 2 | ||||||||||
| 2 – 3 | ||||||||||
| 2 – 4 | 0,5 | |||||||||
| 2 – 5 | 0,23 | |||||||||
| 3 – 5 | ||||||||||
| 3 – 6 | ||||||||||
| 4 – 6 | ||||||||||
| 4 – 9 | 0,34 | |||||||||
| 5 – 8 | 0,58 | |||||||||
| 6 – 7 | ||||||||||
| 7 – 8 | ||||||||||
| 8 – 9 | ||||||||||
| 9 – 10 |
Сетевое планирование в условиях неопределенности
В случаях, когда время выполнения работ точно не известно, то есть продолжительность работы является случайной величиной, для ее определения, на основе экспертного опроса даются три временные характеристики (оценки времени выполнения работ):
1. Оптимистическая (минимальная) оценка toij.
2. Пессимистическая (максимальная) оценка tnij.
3. Наиболее вероятная оценка tн.вij.
Тогда среднее (ожидаемое) время выполнения работы определяется выражением
toжij = 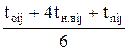 ,
,
или, если известны только крайние оценки:
toжij = 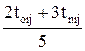 .
.
Тема 2. Элементы теории массового обслуживания
Основные понятия теории массового обслуживания. Предметом изучения теории массового обслуживания (ТМО) являются процессы, в которых, с одной стороны, возникают запросы на выполнение каких-либо работ или услуг, а с другой стороны – производится удовлетворение этих запросов. Такие процессы реализуются в системах массового обслуживания (СМО).
Та часть СМО, в которой возникают запросы, называется обслуживаемой подсистемой, а та часть СМО, которая принимает запросы и удовлетворяет их, называется обслуживающей подсистемой.
Каждый отдельный запрос на выполнение какой-либо работы называется заявкой, или требованием. Часть обслуживаемой подсистемы, которая в любой момент времени может послать только одно требование, называется источником требования, или объектом обслуживания. Обслуживанием называется удовлетворение поступившего в обслуживающую подсистему требования. Часть обслуживающей подсистемы, которая способна в любой заданный момент времени удовлетворять только одно требование, называется обслуживающим аппаратом. Обслуживающая подсистема – это совокупность однородных обслуживающих аппаратов (контролеров, наладчиков, рабочих, оборудования).
Прикладные задачи ТМО сводятся к тому, чтобы установить оптимальное соотношение между числом поступающих на обслуживание требований и числом обслуживающих устройств, при котором суммарные расходы на обслуживание и убытки от простоя были бы минимальными.
Поток требований – это последовательность возникающих во времени требований. Различают входящий и выходящий потоки и требований. По характеру потоки требований могут быть регулярными и стохастическими (вероятностными). В большинстве случаев входящий поток неуправляем и зависит от случайных факторов, т.е. и число требований, поступающих в систему в единицу времени, и интервал между требованиями – случайные величины.
Среднее число требований, поступающих в систему обслуживания в единицу времени, называется интенсивностью поступлений (l) и определяется по формуле
l = 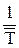 , (1)
, (1)
где  - среднее значение интервала между поступлениями очередных требований.
- среднее значение интервала между поступлениями очередных требований.
СМО с простейшими потоками требований обладают следующими свойствами: стационарностью, ординарностью и отсутствием последействия.
Стационарным называется поток, характер которого с течением времени не меняется.
Ординарным называется такой поток, в котором в любой момент времени может поступить не более одного требования.
Потоком без последействия называется поток, в котором вероятность поступления определенного числа требований после какого-то произвольного времени t не зависит от числа требований, поступивших в систему до этого момента времени.
Если поток требований простейший, то его можно описать количественно с помощью функции Пуассона:
Рк(t) = 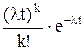 , (2)
, (2)
где Рk(t) – вероятность того, что в течение времени t в систему поступит точно k требований на обслуживание (k = 0,1,2 …).
Математически наличие простейшего потока требований можно определить с помощью статистической обработки данных. Одним из признаков закона распределения Пуассона является равенство математического ожидания случайной величины и ее дисперсии
lt = s2, (3)
где lt – среднее число требований, поступивших на обслуживание за время t.
Время обслуживания – это период, в течение которого удовлетворяется требование на обслуживание. Время нахождения требования в системе состоит из времени обслуживания и времени ожидания обслуживания. Время обслуживания одного требования – это случайная величина, характеризующаяся законом распределения, который определяется на основе статистических испытаний. На практике чаще всего исходят из гипотезы о показательном законе распределения времени обслуживания, в котором плотность распределения убывает с возрастанием времени.
При показательном законе распределения времени обслуживания функция распределения F(t)обсл, представляющая собой вероятность того, что время обслуживания будет меньше заданной величины t, описывается следующим образом:
F(t)обсл = 1 – е-nt, (4)
где n - параметр системы обслуживания, величина, обратная среднему времени обслуживания, представляет собой интенсивность обслуживания одного требования одним аппаратом:
n = 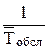 , (5)
, (5)
где 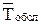 - среднее время обслуживания одного требования одним аппаратом.
- среднее время обслуживания одного требования одним аппаратом.
Параметр системы массового обслуживания a
a = 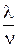 , или a = l ×
, или a = l × 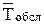 . (6)
. (6)
Параметр a показывает количество требований, поступающих в систему за среднее время обслуживания одного требования одним аппаратом. Поэтому количество обслуживающих аппаратов n не должно быть меньше a:
n ³ a. (7)
Если это требование не выполняется, то очередь будет расти и заявки не будут полностью выполнены.
Date: 2015-07-24; view: 1288; Нарушение авторских прав