Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Метод построения переходных функций с использованием формулы обратного преобразования Лапласа
|
|
Оригинал переходной функции может быть получен использованием формулы обратного преобразования Лапласа, так называемой формулы разложения, которая в общем случае имеет вид
,
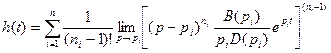где p i – корни уравнения pD(p)=0, ni - кратность корней. В случае только простых корней, когда среди них имеется m вещественных корней и l пар комплексно – сопряженных корней, формула разложения принимает вид
.
В этом выражении ak и bk – вещественная и мнимая части комплексно – сопряженных корней, а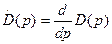 
. Амплитуда и фаза колебательных составляющих определяются следующим образом:
,
; 
.
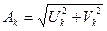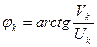При вычислениях по приведенным выше формулам, в первую подставляется только один из пары комплексно – сопряженных корней. При вычислении фазового сдвига необходимо учитывать квадрант, в котором находится вектор Akejjk.
Пример. Построить переходную функцию замкнутой системы.
Передаточная функция замкнутой системы имеет вид
,
где все коэффициенты заданы или вычислены ранее. Корни характеристического уравнения равны:
; 
;
. 
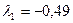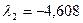1) Построение переходной функции табличным методом.
Изображение переходной функции можно представить в виде:
,
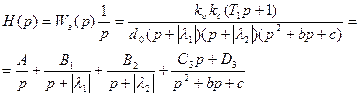где b=2a, c=a2+b2.
Приведем полученное выражение к общему знаменателю и приравняем числитель этого выражения к числителю исходного изображения переходной функции. Приравняв члены при одинаковых степенях оператора p в правой и левой частях, получим систему линейных уравнений относительно неопределенных коэффициентов. Из этой системы сразу определяется А=1, после чего решается система 4-го порядка.
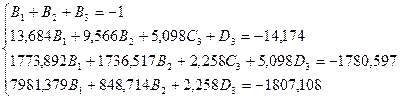
Решение этой системы дает:
; 
;
; 
.
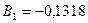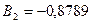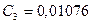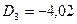Три первых слагаемых изображения переходной функции являются табличными. Необходимо преобразовать к табличному виду четвертое слагаемое.
.
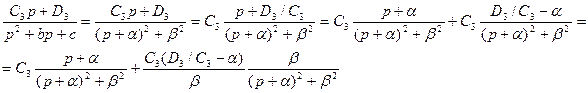Полученные слагаемые являются табличными. Подставив численные значения параметров и использовав таблицы преобразования Лапласа, получим выражение для переходной функции
.
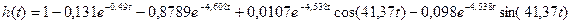2) Построение переходной функции с использованием формулы разложения.
Вначале определим составляющие процесса, соответствующие вещественным корням.
; 
.
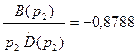Для колебательной составляющей получим
, 
.
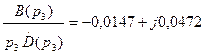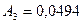Так как вектор этой составляющей находится во втором квадранте, то
.
Следовательно
.
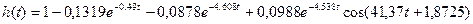Переходные процессы, полученные различными способами, совпадают с точностью до арифметических вычислений. Кривая переходной функции показана на рис.15. Переходный процесс практически монотонный. Колебательная составляющая фактически никак себя не проявляет ввиду крайне малой амплитуды. Перерегулирование отсутствует: s =0. Время регулирования, определенное при D=0,05, приближенно равно 2,2 с., что для системы автоматического регулирования большинстве случаев является вполне приемлемым.
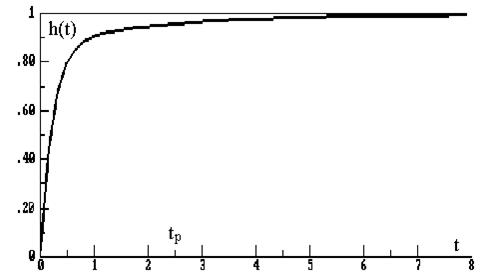
Рис.15. Переходная функция системы регулирования
Date: 2015-07-24; view: 643; Нарушение авторских прав