Коэффициенты ошибок

Точность САУ в установившемся режиме, при относительно медленно изменяющихся воздействиях, может быть оценена с помощью коэффициентов ошибок. Изображение ошибки определяется выражением

,

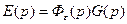где - передаточная функция по ошибке.

Разложим передаточную функцию системы по ошибке в степенной ряд в окрестности точки p=0. Отметим, что при p®0, t®¥ и именно поэтому мы говорим о точности в установившемся режиме.

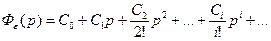
Обозначим: 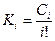и получим

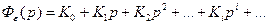, (8)

.

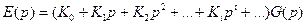Учитывая, что оператор p, умноженный на изображение самой величины, является символом дифференцирования, можно для оригиналов записать

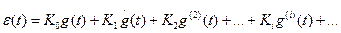. (9)

Выражение (9) определяет зависимость ошибки регулирования от различных составляющих входного воздействия, коэффициенты K_i получили название коэффициентов ошибок:

- K₀ - коэффициент ошибки по положению;

- K₁ - коэффициент ошибки по скорости;

- K₂ – коэффициент ошибки по ускорению и т.д.

Из (8) следует, что

.

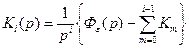Численные значения коэффициентов ошибок определяются из этого выражения при p®0.

.

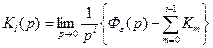Очевидно, что К₀=Ф_e(0).

Входное воздействие можно представить в виде степенного ряда

,

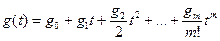где g₀ – постоянная величина, характеризующая начальное значение, g₁=const – скорость изменения входного воздействия, g₂ =const – ускорение и т.д.

Тогда

.

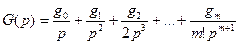Пусть передаточная функция разомкнутой системы имеет вид

,

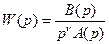где n - порядок астатизма системы. Для передаточной функции замкнутой системы по ошибке получим

.

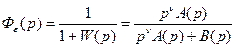Изображение ошибки запишется в виде

.

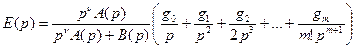Отсюда следует, что если порядок астатизма больше порядка старшей производной воздействия, т.е. n>m, то ошибка в установившемся режиме будет равна нулю. Если n=m, то установившаяся ошибка будет равна постоянной величине, называемой статической ошибкой. И если n<m, то при t®¥ и e®¥. В отношении коэффициентов ошибок последнее выражение позволяет сделать следующие выводы.

1). Если система статическая, т.е .n=0, то существуют все составляющие ошибки и все коэффициенты ошибок не равны нулю, т.к. К₀ = Ф_e(0)¹ 0.

2).Система с астатизмом 1-го порядка, n =1, не имеет ошибки по положению и К₀=0.

3).Система с астатизмом 2-го порядка, n =2, не имеет ошибок по положению и по скорости и К₀ =0, К₁=0.

Этот список можно продолжить. Таким образом, повышение порядка астатизма повышает точность системы в установившемся режиме. Но повышение порядка астатизма снижает запасы устойчивости, т.к. введение интегрирующих звеньев увеличивает фазовое запаздывание (снижает частоту wp). Поэтому на практике порядок астатизма выше второго не применяют, а чаще всего ограничиваются астатизмом первого порядка, используя для повышения точности другие способы.

Date: 2015-07-24; view: 917; Нарушение авторских прав