
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Блок 11. Малая выборка
|
|
Малая выборка – это несплошное статистическое наблюдение, при котором выборочная совокупность образуется из сравнительно небольшого числа единиц генеральной совокупности. Обычно объем малой выборки не превышает 30 единиц, а минимальный объем может доходить до 4-5 единиц. В отдельных случаях к малой может быть отнесена выборка до 45 единиц. Малая выборка широко применяется в экономических исследованиях и при организации контроля качества товаров и услуг.
Средняя ошибка малой выборки определяется по формуле:
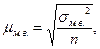 где
где 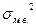 - дисперсия малой выборки, она рассчитывается по формуле
- дисперсия малой выборки, она рассчитывается по формуле
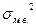 =
= 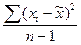 , где n-1 - число степеней свободы.
, где n-1 - число степеней свободы.
Предельная ошибка малой выборки рассчитывается по формуле:
 Коэффициент доверия t зависит не только от заданной доверительной вероятности, но и от численности единиц выборки n. Для отдельных значений t и n доверительная вероятность малой выборки определяется по специальным таблицам Стьюдента, где даны распределения стандартизированных отклонений:
Коэффициент доверия t зависит не только от заданной доверительной вероятности, но и от численности единиц выборки n. Для отдельных значений t и n доверительная вероятность малой выборки определяется по специальным таблицам Стьюдента, где даны распределения стандартизированных отклонений:
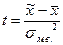 .
.
Для проведения малой выборки в качестве доверительной вероятности принимается 0,95 и 0,99. Для определения предельной ошибки малой выборки используют распределения Стьюдента и определяют коэффициент доверия t:
| n | S(t) | |
| 0,95 | 0,99 | |
| 3,183 2,777 2,571 2,447 2,364 2,307 2,263 2,119 2,078 | 5,841 4,604 4,032 3,707 3,500 3,356 3,250 2,921 2,832 |
Пример. При анализе прибыли по сделкам, совершенным фирмой в течение года, была сделана выборка и установлена по ним прибыльность в %: 4,5; 5,0; 4,2; 3,5; 6,0; 5,2; 4,5; 5,2; 4,3; 6,6.
Нужно по данным выборочного наблюдения установить с вероятностью 0,95 предел, в котором находится средняя прибыльность сделок, по результатам работы фирмы за год.
Средняя прибыльность сделок по данным малой выборки:
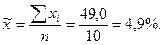 Определяем дисперсию малой выборки; для этого произведем предварительные расчеты:
Определяем дисперсию малой выборки; для этого произведем предварительные расчеты:
Прибыльность сделок
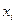
|
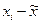
|
(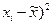
|
| 4,5 5,0 4,2 3,5 6,0 5,2 4,5 5,2 4,3 6,6 | -0,4 0,1 -0,7 -1,4 1,1 0,3 -0,4 0,3 -0,6 1,7 | 0,16 0,01 0,49 1,96 1,21 0,09 0,16 0,09 0,36 2,89 |
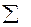 49,0 49,0
| - | 7,42 |
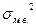 =
= 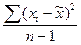 =
= 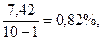
Определяем среднюю ошибку малой выборки:
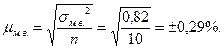
Находим предельную ошибку малой выборки. Для этого по распределению Стьюдента при заданной вероятности 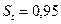 находим значение коэффициента доверия t= 2,263
находим значение коэффициента доверия t= 2,263
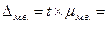 2,263
2,263 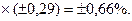
Следовательно, с вероятностью 0,95 можно утверждать, что средняя годовая прибыльность сделок фирмы находится в пределах:
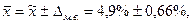 т.е. от 4,9-0,66= 4,24% до 4,9+0,66= 5,56%.
т.е. от 4,9-0,66= 4,24% до 4,9+0,66= 5,56%.
Date: 2015-07-24; view: 514; Нарушение авторских прав