
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Де - деяка функція
|
|
Необхідно знайти корені рівняння, тобто всі значення 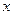 , які після підстановки їх в рівняння перетворюють його в тотожність.
, які після підстановки їх в рівняння перетворюють його в тотожність.
Відносно невелику кількість задач знаходження коренів алгебраічних рівнянь можна розв’язати аналітично. На практиці ж майже завжди доводиться шукати розв’язок за допомогою чисельних методів.
Для розв’язування алгебраічних рівнянь в системі MathCad використовується спеціальний обчислювальний блок Givtn/Find (Дано/Знайти), який складається із трьох частин, записаних послідовно одна за одною:
· Given- ключове слово;
· Рівняння, записане за допомогою логічних операторів;
· Find(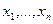 ) – вбудована функція для розв’язування рівняння.
) – вбудована функція для розв’язування рівняння.
Вставляти логічні оператори потрібно з панелі інструментів Boolean. Якщо ви хочете ввести логічний знак дорівнює з клавіатури, то необхідно натиснути комбінацію клавіш <Ctrl>+<=>. Значення функції Find Буде представляти собою матрицю із можливих розв’язків по кожній змінній, причому кількість рядків цієї матриці буде дорівнювати числу аргументів функції Find. Пояснимо сказане на прикладі.
Приклад 1. Аналітичний розв’язок кубічного рівняння
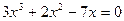
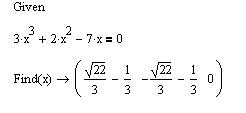
Приклад 2. Аналітичний пошук нулів функції 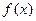
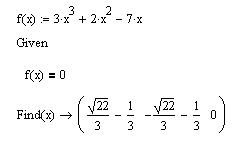
Для розв’язування рівняння з одним невідомим в MathCad крім обчислювального блоку Givtn/Find передбачена вбудована функція root, яка в залежності від типу задачі, може містити або два, або чотири аргументи і, відповідно, використовувати різні алгоритми пошуку коренів рівняння:
· root(f(x),x)
· root(f(x), x, a, b)
Приклад 3. Розв’язати нелінійне рівняння 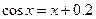 :
:
· привести рівняння до вигляду: права частина =0;
· протабулювати функцію 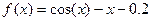 на проміжку
на проміжку 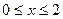 з кроком
з кроком 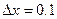 ;
;
· побудувати графік функції, на екрані отримати:
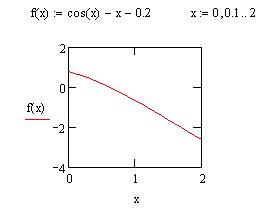
· на графіку визначити наближене значення кореня рівняння x=0.6;
· використати функцію Root(f(x),x), на екрані отримати:
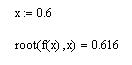
· розв’язок рівняння: 0.616.
4. Розв’язування систем лінійних алгебраічних рівнянь
Розв’язування систем лінійних алгебраічних рівнянь є однією з головних проблем обчислювальної лінійної алгебри. Задачу розв’язування системи лінійних алгебраічних рівнянь можна записати в матричній формі  , де
, де 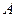 – матриця коефіцієнтів СЛАР,
– матриця коефіцієнтів СЛАР, 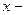 вектор невідомих,
вектор невідомих, 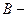 вектор правих частин рівнянь. З курсу лінійної алгебри відомо, що така система має єдиний розв’язок, якщо матриця A невироджена, або несингулярна, тобто її визначник не дорівнює нулю.
вектор правих частин рівнянь. З курсу лінійної алгебри відомо, що така система має єдиний розв’язок, якщо матриця A невироджена, або несингулярна, тобто її визначник не дорівнює нулю.
Найпростіший спосіб розв’язування будь-якої несингулярної системи- використання алгоритму Гауса, який реалізований в системі Mathсad у вбудованій функції lsolve.
Приклад 1. Розв’язати СЛАР 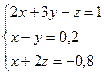 за допомогою функції lsolve.:
за допомогою функції lsolve.:
· Сформувати матрицю коефіцієнтів при змінних А:
a) набрати А:;
b) виконати комнду Матрица в меню Вставка (або натиснути кнопку  палітри векторів та матриць);
палітри векторів та матриць);
c) задати потрібне число рядків та стовпців (3 рядки, 3 стовпці);
d) натиснути кнопку Вставить;
e) заповнити мітки потрібними величинами. Натискання на клавішу Тав здійснює переміщення до інших місцезаповнювачів;
f) на екрані отримати 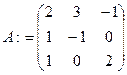 .
.
· Сформувати матрицю-стовпець (вектор) вільних членів, на екрані отримати
 ;
;
· отримати результат з використанням функції lsolve
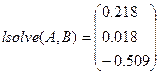 .
.
Розв’язування СЛАР матричним способом
Приклад 2. Розв’язати СЛАР 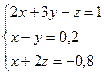 матричним способом:
матричним способом:
Сформувати матрицю коефіцієнтів при змінних А:
a) Набрати А: та виконати комнду Матрица в меню Вставка (або натиснути кнопку  палітри векторів та матриць);
палітри векторів та матриць);
b) задати потрібне число рядків та стовпців (3 рядки, 3 стовпці);
c) натиснути кнопку Вставить;
d) заповнити мітки потрібними величинами. Натискання на клавішу Тав здійснює переміщення до інших місцезаповнювачів;
e) на екрані отримати 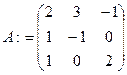 .
.
· Сформувати матрицю-стовпець (вектор) вільних членів, на екрані отримати
 ;
;
· Знайти вектор невідомих (розв’язок системи):
- набрати 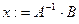
- отримати результат 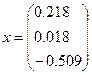 ;
;
- зробити перевірку: 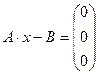 .
.
Розв’язування СЛАР за допомогою обчислювального блоку Given /Find
Для того, щоб чисельним методом розв’язати СЛАР, необхідно після ключового слова given виписати систему, користуючись логічними операторами. Дуже важливо при використанні обчислювального блоку Given /Find всім невідомим необхідно присвоїти початкові значення.
Приклад 3. Розв’язати СЛАР 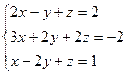 таким чином:
таким чином:
· задати початкові значення невідомих (як правило, ці значення формують із вільних членів системи). Ввести: 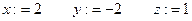
· ввести блок (знак “=” в рівняннях системи вводиться не з клавіатури, а з палітри відношень та бульових функцій):
given
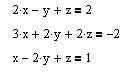
find(x,y,z)= 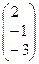 .
.
Розв’язування систем нелінійних алебричних рівнянь розглянемо на прикладі.
Приклад 4. Розв’язати систему нелінійних рівнянь
 таким чином:
таким чином:
· зводимо кожне з рівнянь до виду
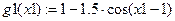 та
та
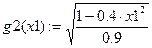
· табулюємо функції 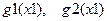 на проміжку
на проміжку 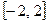 та будуємо графіки функцій:
та будуємо графіки функцій:
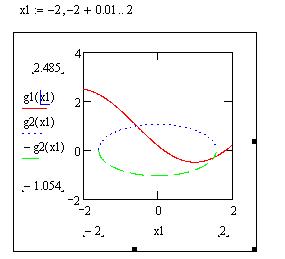
· на графіку визначаємо наближення до коренів та знаходимо розв’язок за допомогою блоку Given/Find:
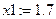
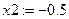
Given
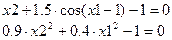 (знак “=” в рівняннях системи вводиться з панелі Boolean)
(знак “=” в рівняннях системи вводиться з панелі Boolean)
Find(x1,x2)= 
Date: 2015-07-24; view: 714; Нарушение авторских прав