Пример анализа устойчивости по критерию Гурвица

Анализ статической устойчивости электрических систем путем прямого отыскания корней характеристического уравнения связан с практическими трудностями, поскольку отсутствуют аналитические выражения для корней уравнений выше четвертого порядка. Однако для суждения об устойчивости системы достаточно знать, что все корни расположены в левой полуплоскости комплексной плоскости, т.е. имеют отрицательную вещественную часть.

Условия, которые позволяют судить о наличии отрицательной вещественной части всех корней характеристического уравнения называются критериями устойчивости. Критерии устойчивости делятся на алгебраические и частотные.

Рассмотрим применение алгебраического критерия Гурвица для анализа статической устойчивости простейшей электрической системы: станция - шины бесконечной мощности, рассмотренной в разд. 3.2. При этом учтем не только демпфирующие моменты, но и переходные процессы в обмотке возбуждения генератора.

В этом случае характеристическое уравнение будет иметь третий порядок [4]

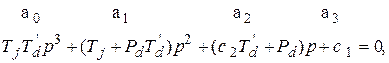(3.10)

где - 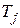постоянная инерции генератора; 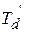- переходная постоянная времени генератора по продольной оси; 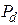- коэффициент демпфирования.

Значение коэффициента 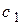вычисляется по (3.4), а для определения 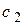используется выражение из [4]:

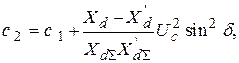(3.11)

где - переходное реактивное сопротивление генератора по продольной оси;

.

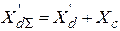Переходная постоянная времени генератора 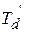рассчитывается из выражения

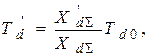(3.12)

где 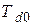- постоянная времени обмотки возбуждения синхронной машины при разомкнутой обмотке статора. Произведем расчет коэффициентов характеристического уравнения (3.10), используя исходные данные примера разд. 3.2 и дополнительные справочные характеристики генератора в относительных единицах [7]:

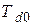= 7.26 = 0.172.

Находим 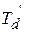по (3.12)

;

,

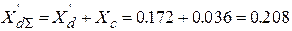тогда

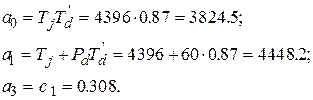
Найдем значение коэффициента 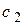по (3.11)

,

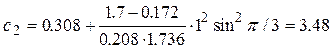тогда .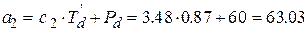

Запишем характеристическое уравнение (3.10) с учетом значений коэффициентов:

(3.13)

Для использования Гурвица составим определитель Гурвица по следующим правилам:

- по главной диагонали располагаются коэффициенты уравнения (3.10) в порядке возрастания индексов, начиная с ;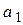

- построчно помещаются коэффициенты только с четными или только с нечетными индексами; влево от диагонали индексы уменьшаются, а вправо увеличиваются;

- все недостающие коэффициенты заменяются нулями.

Определитель Гурвица для характеристического уравнения (3.13) имеет вид:

Выделим миноры относительно главной диагонали и применим критерий Гурвица: для устойчивости системы необходимо и достаточно, чтобы при 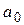>0 все главные диагональные миноры определителя Гурвица были положительны.

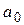= 3824.5>0;

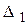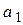= = 448.2>0;

;

.

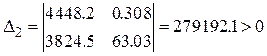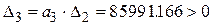Таким образом, рассмотренная электрическая система является статически устойчивой.

Date: 2015-07-24; view: 564; Нарушение авторских прав