
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Характеристического уравнения
|
|
Установившийся режим работы электроэнергетических систем предполагает непрерывное, стохастическое изменение во времени большого количества нагрузок. Это приводит к появлению на генераторах системы дополнительных малых моментов DM, которые также стохастически увеличивают и уменьшают моменты, действующие на валах этих генераторов и смещающие их роторы на малые углы Dd. Возникающие при этом переходные процессы могут быть описаны дифференциальными уравнениями относительно малых Dd. Порядок уравнений определяется сложностью рассматриваемой электрической системы.
Рассмотрим простейший случай:
|
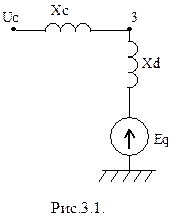
Станция - шины бесконечной мощности. Проанализируем статическую устойчивость системы (рис.2.5) при отсутствии нагрузки в узлах 1, 2, 4 и подключении к узлу 3 синхронного неявнополюсного генератора. Для решения этой задачи целесообразно привести исходную расчетную схему (рис.2.5) к эквивалентному виду (рис.3.1).
Если не учитывать переходные процессы в обмотке возбуждения генератора, но учесть демпфирующие моменты, дифференциальное уравнение относительно Dd имеет вид [4]:
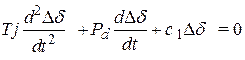 (3.3)
(3.3)
где 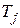 - постоянная инерции [4,6];
- постоянная инерции [4,6]; 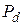 - коэффициент демпфирования[4,6].
- коэффициент демпфирования[4,6].
Коэффициент уравнения 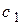 (3.3) определяется исходя из соотношения
(3.3) определяется исходя из соотношения
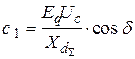 , (3.4)
, (3.4)
где 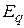 - синхронная ЭДС;
- синхронная ЭДС; 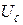 - напряжение системы; d- угол между векторами
- напряжение системы; d- угол между векторами 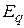 и
и 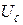 . Значение
. Значение 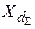 определяется по формуле
определяется по формуле
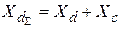 , (3.5)
, (3.5)
где 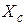 - расчетное эквивалентное сопротивление системы;
- расчетное эквивалентное сопротивление системы; 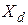 - синхронное индуктивное сопротивление генератора по продольной оси. Тогда характеристическое уравнение имеет вид:
- синхронное индуктивное сопротивление генератора по продольной оси. Тогда характеристическое уравнение имеет вид:
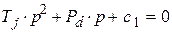 (3.6)
(3.6)
Определив значения корней характеристического уравнения (3.6), на основе теоремы Ляпунова можно судить об устойчивости системы.
Зададимся исходными параметрами генератора [7] и системы. Расчет будем вести в относительных единицах:
 , - базисные значения
, - базисные значения
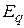 =1.07,
=1.07, 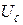 =1,
=1, 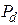 =60,
=60, 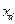 =1,7
=1,7 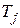 = 14 с - для всех вариантов задания
= 14 с - для всех вариантов задания
 - задается по вариантам
- задается по вариантам 
Для определения коэффициента 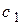 по (3.4) необходимо рассчитать значение эквивалентного сопротивления системы
по (3.4) необходимо рассчитать значение эквивалентного сопротивления системы 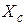 , которое соответствует диагональному элементу матрицы узловых сопротивлений
, которое соответствует диагональному элементу матрицы узловых сопротивлений 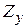 ,
, 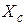 =
= 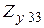 , так как генератор подключен к узлу 3.
, так как генератор подключен к узлу 3.
Матрица узловых сопротивлений 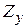 , обратная по отношению к матрице узловых проводимостей
, обратная по отношению к матрице узловых проводимостей 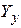 , поэтому выполняется соотношение
, поэтому выполняется соотношение
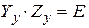 (3.7)
(3.7)
где  - единичная матрица;
- единичная матрица;
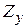 =
= 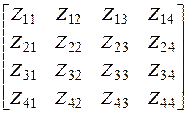 - матрица узловых сопротивлений (рис. 2.5)
- матрица узловых сопротивлений (рис. 2.5)
Отсюда следует матричное уравнение для определения элемента 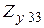
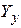
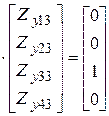 (3.8)
(3.8)
При решении системы уравнений (3.8) воспользуемся результатами расчета узловых напряжений методом Гаусса по матричному уравнению (2.7-2.10). Поскольку матрица коэффициентов одинаковая 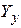 , заменим вектор неизвестных
, заменим вектор неизвестных 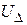 в (2.5) на столбец
в (2.5) на столбец 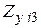 , а столбец свободных членов
, а столбец свободных членов 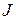 на столбец единичной матрицы. Тогда все преобразования до третьего ключевого уравнения не изменятся.
на столбец единичной матрицы. Тогда все преобразования до третьего ключевого уравнения не изменятся.
Запишем преобразованную систему, начиная с третьего ключевого уравнения:
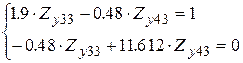 (3.9)
(3.9)
Завершим прямой ход Гаусса:
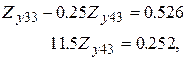
тогда 
Переведем 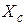 и
и 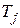 в относительные единицы:
в относительные единицы:
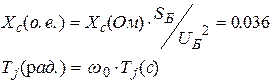
где 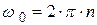 -синхронная угловая частота.
-синхронная угловая частота.
При 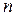 =3000 об/мин -
=3000 об/мин - 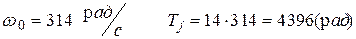
Определим значение коэффициента 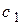
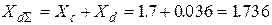
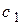 =
= 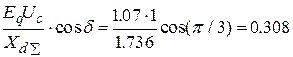
Найдем корни характеристического уравнения вида (3.6)
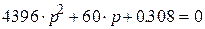
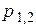 =
= 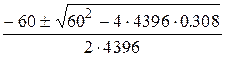 ;
;
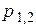 =
= 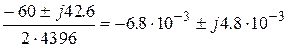
Исходя из теоремы Ляпунова, система является статически устойчивой, поскольку оба корня содержат отрицательную вещественную часть.
Кроме того, по корням характеристического уравнения можно определить вид переходного процесса при отклонении угла Dd (табл.9.1[4]). В рассмотренном примере система колебательно устойчива, изменения Dd(t)имеют вид затухающих гармонических колебаний с частотой около 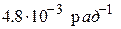 или
или 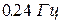
Date: 2015-07-24; view: 520; Нарушение авторских прав