Еркін өшетін тербелістер

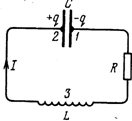
Нақты тербелмелі контурда әрқашанда актив кедергі болады. Контурда жинақталған энергия біртіндеп осы кедергілерде шығындалады, соның есебінен еркін тербеліс өшеді.

1-3-2 тізбек үшін жазылған (3.33) өрнектің түрі (3.3-сурет):

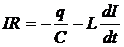. (3.42)

Бұл теңдеуді L-ге бөліп, І-ді q-мен алмастырып, -ны 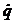-мен белгілеп жазсақ,

(3.43)

3.3-сурет. Нақты тербелмелі контурдың сұлбасы.

теңдеуін аламыз. b= R/2L белгілеу енгізсек және LC-ға кері шама контурдың меншікті циклдік жиілігінің w₀ квадраты екенін ескеріп (3.43) өрнегін мынадай түрда жазуға болады:

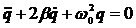. (3.44)

Егер яғни R²/4 L²< 1 / LC болса, онда (3.43)теңдеуінің шешімі:

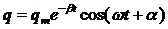(3.45)

болады, мұндағы ; w₀ мен b мәндерін қойсақ:

(3.46)

өрнегін аламыз. Сонымен, өшетін тербелістің циклдік жиілігі контурдың меншікті жиілігінен кіші болады. R=0 болса, онда (3.46)өрнек (3.36)өрнегіне ауысады. (3.45) теңдеуін сыйымдылыққа С бөліп, конденсатордағы кернеуді табамыз:

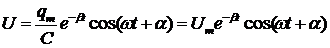. (3.47)

Ток күшін табу үшін (3.45) өрнегін уақыт бойынша дифференциалдаймыз:

.

Бұл формуланың оң жағын бірге тең 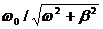шамаға көбейтсек, алатынымыз:

.

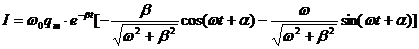Енді

шарттарымен анықталатын y бұрышын енгізіп, ток күшін

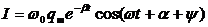(3.48)

түрінде жаза аламыз. Бұл жерде cosy<0, ал sіny>0 болғандықтан мәндері p/2 -ден p -ге дейін аралығында қамтылған. Сондықтан, контурда актив кедергінің болуына байланысты ток күші фаза жағынан кернеуді конденсаторда p/2-ден үлкен шамаға озып отырады. (3.45)функцияның графигі 3.4-суретте көрсетілген.

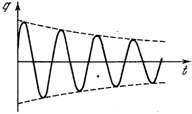
3.4-сурет. Зарядтың уақытқа тәуелділік графигі.

Кернеу мен токтың графиктері де осыған ұқсас. Тербелістің өшуін өшудің логарифмдік декрементімен сипаттау қабылданған.

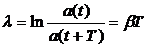, (3.49)

мұндағы а(t) қандай да бір шаманың амплитудасы (q, U, немесе І). Өшудің логарифмдік декременті амплитуда е есе азаятын уақыт ішіндегі N_e тербеліс санына кері екенін ескертеміз: l=1/N_e. (3.49) өрнек(b=R/2L) мәнін қойып және Т-ның орнына 2p/wауыстырып, l үшін мына

l=2pR/2L w = pR/Lw (3.50)

өрнегін аламыз. Жиілік w, демек l контурдың L,C,R параметрлерімен анықталады. Сонымен, өшудің логарифмдік декременті контурдың сипаттамасы болып табылады.

Date: 2015-07-22; view: 1833; Нарушение авторских прав