Энергия ағынының тығыздығы. Умов-Пойнтинг векторы

Максвелл теориясынан мынадай тұжырым жасауға болады: уақыт бойынша айнымалы электр өрісі құйынды магнит өрісін тұдырса, айнымалы магнит өрісі құйынды электр өрісін тудырады. Бұл екі өріс өзара тығыз байланысты, сондықтан бұл құбылыс электрмагниттік өріс деп аталады. Электрмагниттік өріс кеңістіктің белгілі бір жерінде өзгермей тұра алмайды. Кеңістіктің қандайда бір нүктесінде қоздырылған айнымалы электр өрісі айнымалы магнит өрісін тұдырса, өз кезегінде айнымалы магнит өрісі айнымалы электр өрісін қоздырады. Олай болса, бүл құбылыс қайталанып отыратындықтан, кеңістікте электр және магнит өрістерінің кезектескен түрленуі, оның бір нүктесінен келесі бір нүктесіне тарайды. Бұл құбылыс кеңістікте уақыт бойынша периодты өтеді, өрістердің кеңістікте таралуын электрмагниттік толқын деп атаймыз. Электрмагниттік толқынның пайда болуы және қасиеттері Максвелл теңдеулері арқылы анықталады.

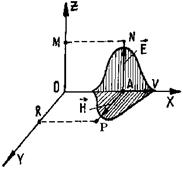Электрмагниттік толқын ашық тербеліс контурында пайда болады, оның қозуы үшін кез келген электр өткізгіш арқылы айнымалы ток өтсе де жеткілікті. Координаттар осінің бас нүктесінде орналасқан өткізгіштен төмен бағытталған айнымалы ток өткенде, онда пайда болған электрмагниттік ұйытқу суретте көрсетілген. Мұндағы магнит өрісінің кернеулігі, ал 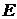электр өрісінің кернеулігі. Қозғалмайтын ОАNM және ОАРR контурларын қарастырайық. Олар үшін Максвелл теңдеулерінің түрлері төмендегідей болар еді:

3.1-сурет. Электрмагниттік

толқынның таралуы.

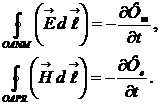(3.20)

Контурлар жақтарының ұзындығын AN=AP= l деп алайық. Осы контур бойында Е_і мен Н_інөлге тең емес болғандықтан, (3.20) теңдеулері былай түрленеді:

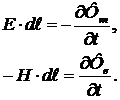(3.21)

Егер қарастырылып отырған электромагниттік ұйытқудың таралу жылдамдығы v болса, онда ол dt уақыт аралығында dx=vdt қашықтыққа жылжиды. Онда алынған контурлар арқылы өтетін магнит және электр өрістерінің ағыны Ф_m мен Ф_е біршама кемиді:

dФ_m= -Вl∙vdt және dФ_е=-Dl∙vdt.

Сондықтан және деп алуға болады, (3.21)-теңдеуінен шығатын қортынды:

E=v×B, H=v∙D. (3.22)

Жоғарыда келтірілген (3.21) және (3.22) теңдіктерін еске ала отырып, Е және Н үшін мынадай теңдіктер келіп шығады:

E=v mm₀H, H=v ee₀E. (3.23)

Бұл екі теңдеуден толқын жылдамдығының

(3.24)

болатынын анықтау қиын емес. Электрмагниттік ұйытқудың таралу жылдамдығы нақты сан мәнге ие және ол таралу ортасының қасиеттеріне байланысты. Вакуумде e=m=1 екені белгілі. Олай болса, электромагниттік толқынның таралу жылдамдығы v=c:

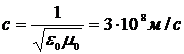, (3.25)

мұндағы e₀ мен m₀ – электр және магнит тұрақтылары.

Электрмагнит толқынның вакуумде таралу жылдамдығы с -ны есептеп табу Максвелл теңдеулерінен алынған ең маңызды қортындылардың бірі болып табылады. Бұл жарықтың электромагниттік тегін көрсетеді. Жоғарыда келтірілген (3.23) өрнектегі Максвелдің бірінші және екінші теңдеулерінен алынған формуланы векторлық түрде жазсақ, онда

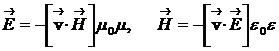. (3.26)

Бұл өрнектегі 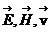векторлары оң бұранда жүйесін құрайды. Электрлік және магниттік кернеулік векторлары өзара перпендикуляр және олардың әрқайсысы ұйытқудың таралу жылдамдығына нормаль бағытталған, яғни .

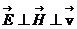Электрмагниттік өріс кеңістікте тарала отырып, энергия тасымалдайды. Электр өрісі энергиясының тығыздығы

,

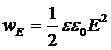ал магнит өрісінің энергия тығыздығы

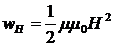
формулаларымен анықталады. Онда электромагниттік өріс энергиясының тығыздығы олардың қосындысына тең:

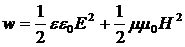. (3.27)

Вакуумде таралған электромагниттік толқын үшін Умов-Пойнтинг векторын S деп белгілесек, ол мынадай өрнекпен анықталады:

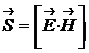. (3.28)

Date: 2015-07-22; view: 4092; Нарушение авторских прав