Оптимальный выбор потребителя

Кривые безразличия графически отражают систему предпочтений потребителя. Естественно потребитель стремится приобрести товарный набор, принадлежащий наиболее удаленной от начала координат кривой безразличия. Однако, это не всегда возможно, т.к. потребительское поведение ограничивается средствами, которыми он располагает.

Если обозначать рыночные цены блага X через Р_х, а блага Y через P_y, а его доход через I, то бюджетное ограничение потребителя можно записать в виде уравнения:

.

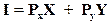Доход потребителя равен сумме его расходов на покупку товаров X и Y.

Преобразуем уравнение и получим уравнение бюджетной линии, которая имеет вид прямой линии (рис. 10). Чем выше доход, тем дальше от начала координат находится линия бюджетного ограничения.

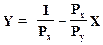
Рис. 10. Бюджетная линия

Пусть задана линия бюджетного ограничения и несколько кривых безразличия. Какой товарный набор выбирает потребитель?

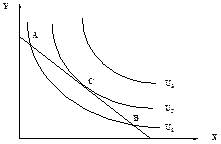
Рис. 11. Оптимальный выбор потребителя

Оптимум потребителя будет в точке С. В рамках бюджетного ограничения индивид постарается так распределить свой доход между различными благами, чтобы максимизировать полезность U. Соответствующий набор благ называется оптимальным планом потребления и обычно обозначается точкой касания бюджетной линии и кривой безразличия.

В точке оптимума выполняется равенство:

Соотношение цены блага X к цене блага Y равно предельной норме замещения блага X блага Y.

В общем случае рассмотрим потребителя (группу семей) с определенным доходом I, предназначенным для приобретения набора товаров X=(x₁,..., x_j ,..., x_n), цены которых соответственно равны P=(p₁,..., p_j ,..., p_n).

Здесь X,P - неотрицательные векторы.

В терминах функции полезности оптимальный набор 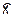соответствует наибольшему значению u(x), т.е. является решением задачи:

u(x) = u(x₁,..., x_j,..., x_n) ® max

при условиях

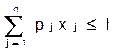; x_j ³ 0 (j = 1,..., n)

При анализе задачи оптимального выбора обычно применяется еще одно важное предположение теории потребления, которое носит название гипотезы ненасыщения.

Это означает, что для “ненасыщаемого” потребителя всякий набор x, который содержит любого продукта столько же, либо (хотя бы по одной позиции) несколько больше, чем набор y, оказывается более предпочтительным. Таким образом, функция полезности является монотонно возрастающей по каждому аргументу x_j.

Если функция полезности имеет производные по своим аргументам, то из предположения о ненасыщаемости (и монотонности u(x)) следует, что все первые частные производные функции полезности являются положительными, т.е.

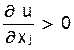(j = 1,..., n)

для любого набора потребительских благ. Величина частной производной

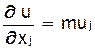
имеет следующий экономический смысл: она показывает, на сколько увеличится полезность набора, если количество потребляемого блага увеличится на “малую единицу”. В связи с этим указанная производная носит название предельной (маргинальной, дифференциальной) полезности.

В экономических исследованиях, как правило, используются некоторые конкретные виды выпуклых функций полезности, причем подбор вида функции и оценка числовых значений параметров производится на основе наблюдений и анализа поведения потребителей. Чаще всего применяются линейная, квадратичная и логарифмическая функции.

Рассмотрим задачу оптимального выбора потребителя для ненасыщаемого потребителя:

Нетрудно заметить, что оптимальный набор 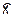( 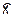₁,..., 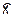_n) необходимо должен удовлетворять бюджетному ограничению как точному равенству. В самом деле, если бы оптимальный набор достигался бы при условии

,

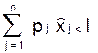то потребитель мог бы купить на оставшиеся деньги некоторое количество любого блага, и тем самым получить новый набор с большей полезностью. Это означает, что внутренняя точка множества не может быть оптимальным набором.

Таким образом, задача об оптимальном наборе имеет вид:

u(x) = u(x₁,..., x_j,..., x_n) ® max

.

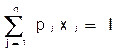Решение этой задачи на условный экстремум находится при помощи метода множителей Лагранжа.

Оптимальный набор определяется путем решения следующей системы из (n+1) уравнения:

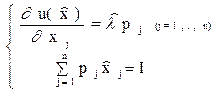
Таким образом, при заданной системе цен потребитель должен выбрать такой набор, а котором все предельные полезности пропорциональны ценам. При этом оптимальное значение множителя Лагранжа 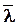часто называют “предельной полезностью денег” и трактуют как прирост максимальной полезности при увеличении дохода I на малую единицу.

Рассмотрим простой пример.

Пусть n=2, функция полезности

u(x₁, x₂) = ln x₁ + ln x₂,

бюджетное ограничение

p₁x₁ + p₂x₂ = I.

Решение задачи оптимального выбора

отсюда:

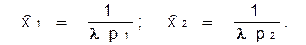
Используя бюджетное ограничение, имеем:

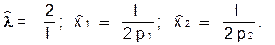
Как видно из приведенного решения оптимальный выбор потребителя имеет очень естественный вид: количество потребляемого блага прямо пропорционально доходу (I) и обратно пропорционально его цене.

В более реалистичных вариантах постановки задачи оптимального выбора при помощи дополнительных условий могут быть учтены ограничения по ассортименту потребляемых товаров и услуг, возможность взаимной замены различных продуктов и т.п.