Задача минимизации издержек производства

Для нахождения оптимальных решений производителю не достаточно знания производственных функций, которые содержат лишь технологическую информацию, так как отсутствует информация о цене продукции и ценах на ресурсы. Пусть q₁, q₂, …..q_n – цены соответственно ресурсов x₁, x₂, ….., x_n. Тогда издержки составят величину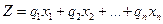

Задача минимизации издержек производства следующая: для заданного объема выпуска продукции y₀ найти такое сочетание ресурсов, чтобы их стоимость (затраты) была минимальной. В математической форме

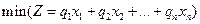
при условиях

Для n=2 решение задачи изображено на рис.

Геометрически формулировка задачи следующая: задана изокванта 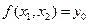и нужно среди линий уровня, называемых изокостами (параллельных прямых) функции 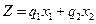, найти касательную к данной изокванте. Точка касания x* и есть оптимальное решение.

Задача решается методом множителей Лагранжа. Функция Лагранжа имеет вид:

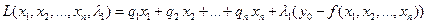
Приравнивая к 0 частные производные функции Лагранжа, получаем систему уравнений

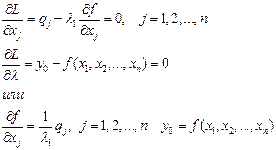
Таким образом, в точке минимума будем иметь:

1. предельные производительности ресурсов пропорциональны их ценам

2. отношение предельных производительностей ресурсов равно отношению их цен

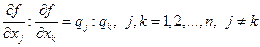
3. отношение предельных производительностей ресурсов к их ценам равны между собой

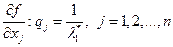
Полученные соотношения составляют основу теории предельной производительности факторов производства как теории стоимости, а именно: цены ресурсов пропорциональны предельным производительностям ресурсов, в частности для труда имеем, что он оценивается в соответствии со своей предельной производительностью.

Дадим интерпретацию множителя Лагранжа.

В точке минимума

следовательно

т.е. l₁^* есть общие предельные издержки на единицу дополнительной продукции.

Date: 2015-07-24; view: 735; Нарушение авторских прав