
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Техническое задание
|
|
В полой трубе прямоугольного сечения (Рис. 1) с идеально проводящими стенками создано монохроматическое электромагнитное поле. Труба заполнена однородной изотропной средой без потерь, абсолютная диэлектрическая и магнитная проницаемости равны 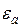 и
и 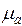 соответственно. Известно, что комплексная амплитуда вектора
соответственно. Известно, что комплексная амплитуда вектора 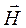 равна:
равна:
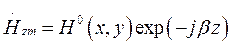 , где
, где  ,
, 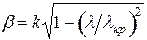 ,
, 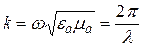 ,
, 
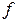 ,
, 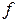 - частота электромагнитных колебаний;
- частота электромагнитных колебаний; 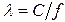 - длина волны, свободно распространяющейся в однородной изотропной непроводящей среде с параметрами
- длина волны, свободно распространяющейся в однородной изотропной непроводящей среде с параметрами 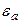 и
и 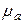 ;
;  - скорость света в этой среде,
- скорость света в этой среде, 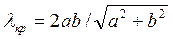 ,
, 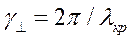
Исходные данные:
| № вар | 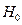 В/м
В/м
| 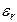
| 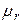
| a см | b см | 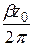
| 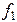 ГГц
ГГц
| 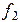 ГГц
ГГц
|
| 2,25 | 0,75 |
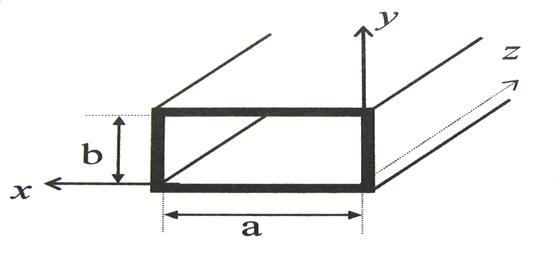

Рис. 1
1)Определение комплексных амплитуд поперечных составляющих вектора 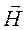 , а затем из уравнений Максвелла определим комплексные амплитуды составляющих вектора
, а затем из уравнений Максвелла определим комплексные амплитуды составляющих вектора 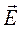 , используя соотношение
, используя соотношение
 ,
,
Найдем комплексные амплитуды составляющих вектора 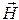 , воспользовавшись вышеприведённым соотношением:
, воспользовавшись вышеприведённым соотношением:
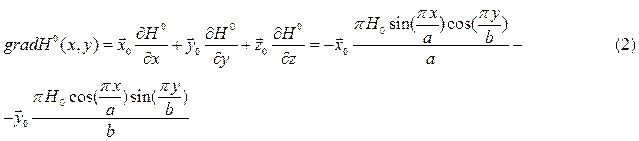
Подставляя значение из (2) в (1) найдём комплексную форму вектора 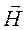 :
:
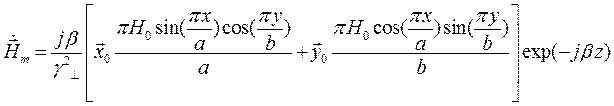
Запишем проекции комплексной амплитуды вектора 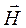 на оси координат:
на оси координат:
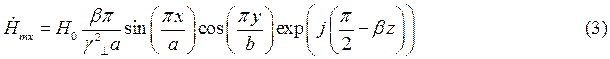
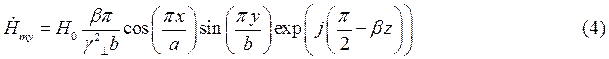
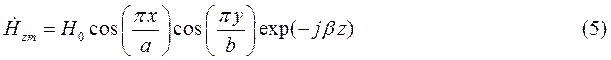
Воспользуемся первым уравнением Максвелла в комплексной форме для определения комплексной амплитуды вектора 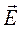 :
:
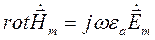 , где
, где  - абсолютная диэлектрическая проницаемость среды,
- абсолютная диэлектрическая проницаемость среды, 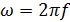 ,
, 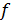 – частота электромагнитных колебаний, тогда отсюда
– частота электромагнитных колебаний, тогда отсюда 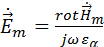
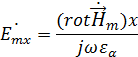
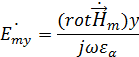
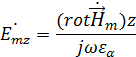
Найдем 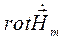 :
:
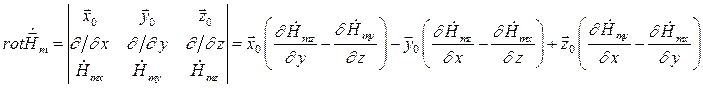
Тогда составляющие комплексной амплитуды вектора  равны соответственно:
равны соответственно:
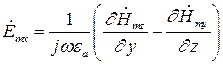 (7)
(7)
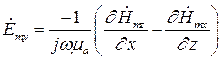 (8)
(8)
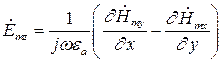
(9)
Найдем выражения для частных производных составляющих комплексной амплитуды вектора 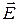 по соответствующим координатам:
по соответствующим координатам:
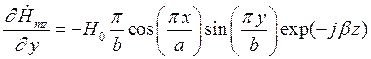
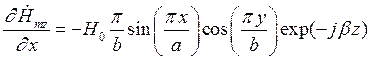
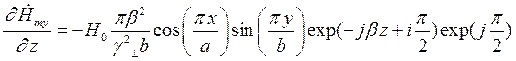
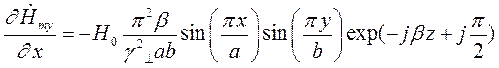
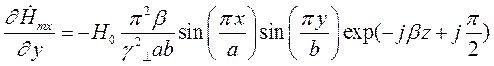
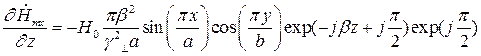
Подставляя найденные значения частных производных в (7), (8) и (9), получим итоговые выражения для комплексных амплитуд составляющих вектора 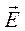 :
:
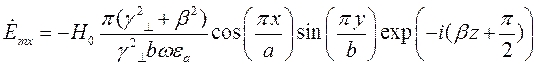 (10)
(10)
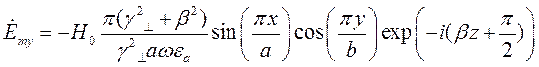 (11)
(11)
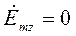 (12)
(12)
2)Определение диапазона частот, в котором 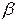 – действительное число, т.е. рассматриваемое поле – бегущая волна.
– действительное число, т.е. рассматриваемое поле – бегущая волна.
По условию задачи 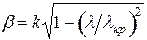 . Значит,
. Значит, 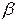 будет действительным в случае, если
будет действительным в случае, если
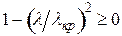 , т.е. при
, т.е. при 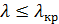
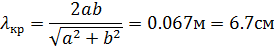
Этому диапазону длин волн соответствует диапазон частот:
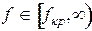 , где
, где 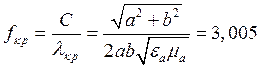 ГГц, где С =
ГГц, где С = 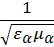 ,
,
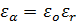
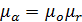
Таким образом, если частота волны не принадлежит рассчитанному диапазону частот, то 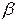 является мнимой величиной. Для этого случая произведем замену:
является мнимой величиной. Для этого случая произведем замену: 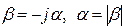 , при этом
, при этом 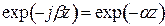 ,
, 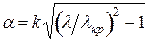
3) Определение мгновенных значений всех составляющих векторов 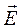 и
и 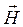 для двух случаев:
для двух случаев:
а) когда 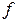 принадлежит найденному в п. 2 диапазону частот
принадлежит найденному в п. 2 диапазону частот
б) когда 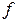 не принадлежит этому диапазону.
не принадлежит этому диапазону.
Для получения выражений для мгновенных значений составляющих векторов поля необходимо домножить их комплексные амплитуды на выражение 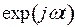 и, выделить действительную часть, то есть:
и, выделить действительную часть, то есть:
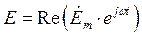 ;
; 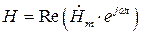
В первом случае выражения для комплексных амплитуд составляющих остаются без изменений. Во втором случае необходимо произвести замену, описанную в п. 2.
При 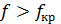 выражения для комплексны амплитуд составляющих магнитного и электрического полей имеют вид:
выражения для комплексны амплитуд составляющих магнитного и электрического полей имеют вид:
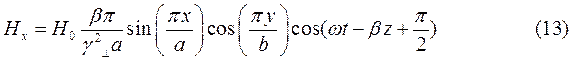
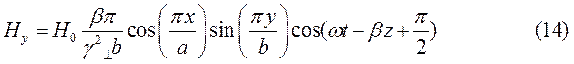
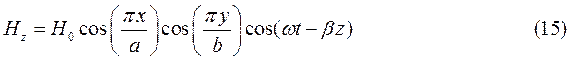
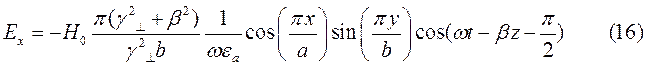
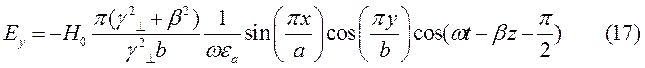
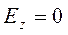
(18)
При 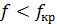 выражения для комплексны амплитуд составляющих магнитного и электрического полей имеют вид:
выражения для комплексны амплитуд составляющих магнитного и электрического полей имеют вид:
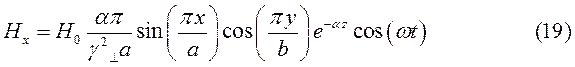
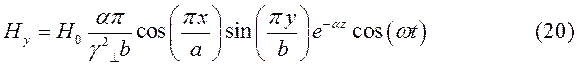
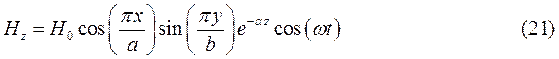
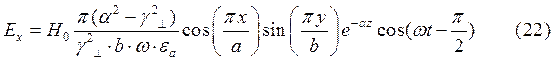
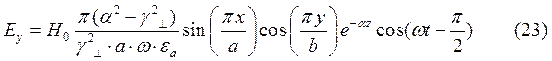
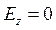 (24)
(24)
4)Построение графиков зависимостей амплитуд составляющих векторов поля на частотах 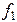 и
и 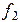 по данным приведенным, в таблице технического задания
по данным приведенным, в таблице технического задания
Вычислим постоянные множители в математическом пакете MathCAD 14, а затем подставим соответствующие значения постоянных величин в выражения с (13) по (24):
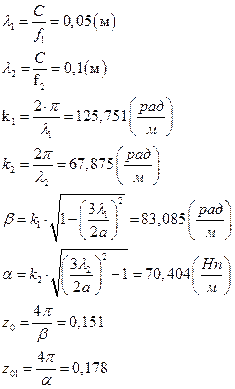 |
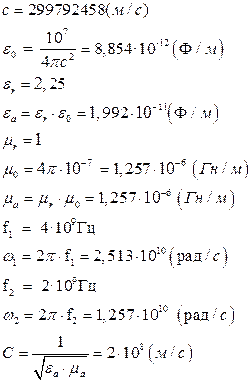
Определение амплитуд составляющих электрического и магнитного полей для Случая 1:
z=z0; y=0,5b; 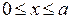 ;
; 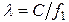
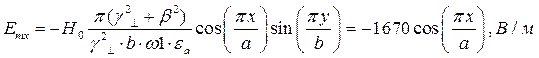
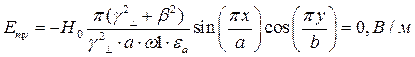
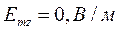
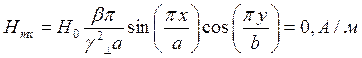
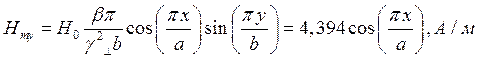
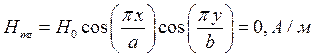
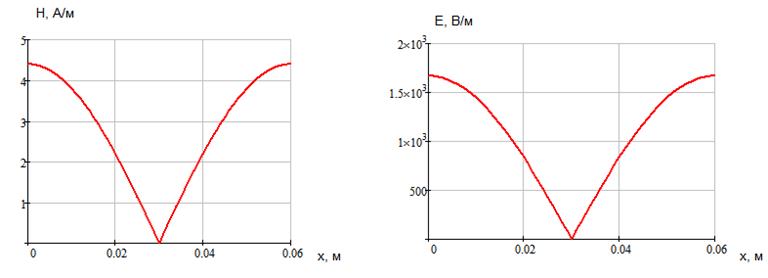
Указанные формулы были запрограммированы в математическом пакете MathCAD 14, где были построены графики данных зависимостей. Результаты показаны на Рис. 2, Рис. 3.
Определение амплитуд составляющих электрического и магнитного полей для Случая 2:
z=z0; y=0,5b; 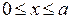 ;
; 
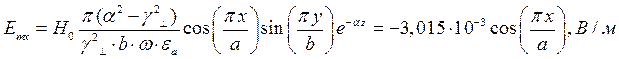
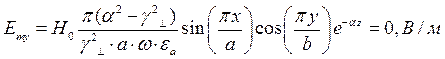
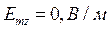
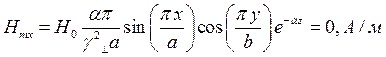
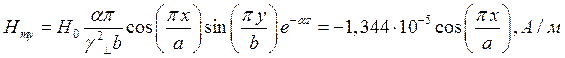
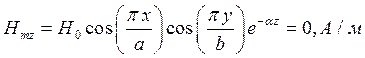
Указанные формулы были запрограммированы в математическом пакете MathCAD 14, где были построены графики данных зависимостей. Результаты показаны на Рис. 4, Рис. 5.
Определение амплитуд составляющих электрического и магнитного полей для Случая 3:
z=z0; x=0,75a; 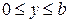 ;
; 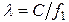
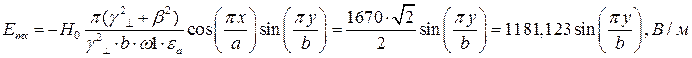
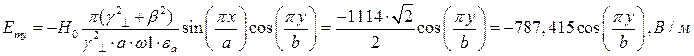
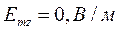
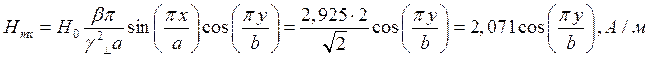
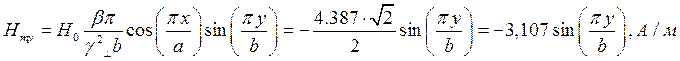
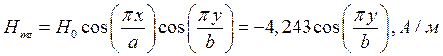
Указанные формулы были запрограммированы в математическом пакете MathCAD 14, где были построены графики данных зависимостей. Результаты показаны на Рис. 6, Рис. 7.
Определение амплитуд составляющих электрического и магнитного полей для Случая 4:
z=z0; x=0,75a; 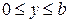 ;
; 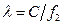
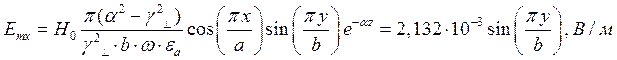
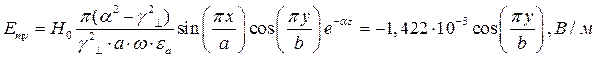
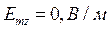
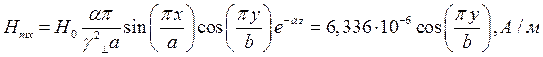
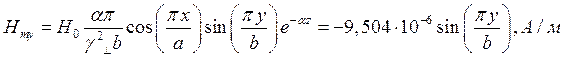
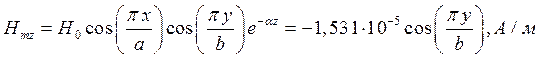
Указанные формулы были запрограммированы в математическом пакете MathCAD 14, где были построены графики данных зависимостей. Результаты показаны на Рис.8, Рис. 9.
Определение амплитуд составляющих электрического и магнитного полей для Случая 5:
x=0,25a; y=0,25b; 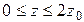 ;
; 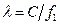
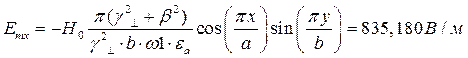
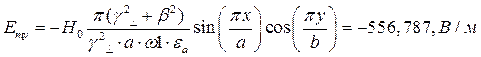
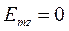

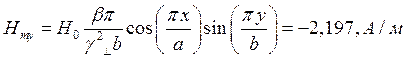
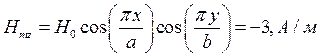
Указанные формулы были запрограммированы в математическом пакете MathCAD 14, где были построены графики данных зависимостей. Результаты показаны на Рис. 10, Рис. 11.
Определение амплитуд составляющих электрического и магнитного полей для Случая 6:
x=0,25a; y=0,25b; 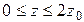 ;
; 
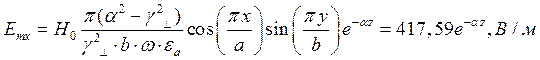
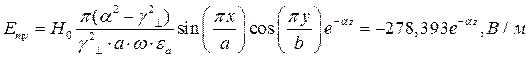
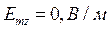
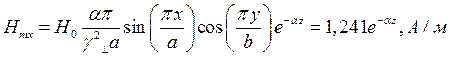
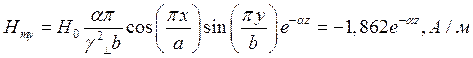
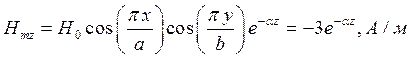
Указанные формулы были запрограммированы в математическом пакете MathCAD 14, где были построены графики данных зависимостей. Результаты показаны на Рис. 12, Рис. 13.
В выражениях для случаев 1, 3, 5  м,
м, 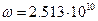 рад/с, z0=0.151 м,
рад/с, z0=0.151 м, 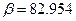 а для случаев. 2, 4, 6
а для случаев. 2, 4, 6 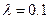 м,
м, 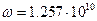 рад/с, z0=0.178 м и
рад/с, z0=0.178 м и 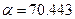 Нп/м.
Нп/м.
 ---
---
 |  | ||||||||||
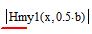 | |||||||||||
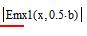 | |||||||||||
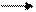 | |||||||||||
 | |||||||||||
Рис. 2 Рис. 3
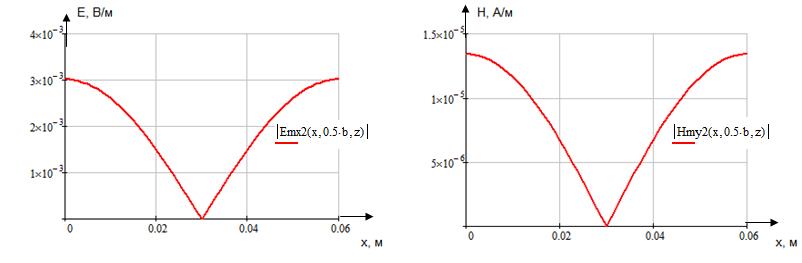
Рис. 4 Рис. 5
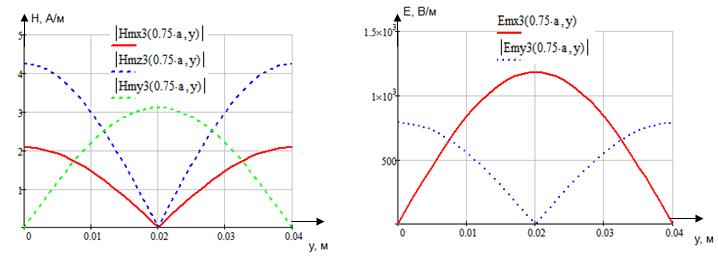
Рис. 6 Рис. 7
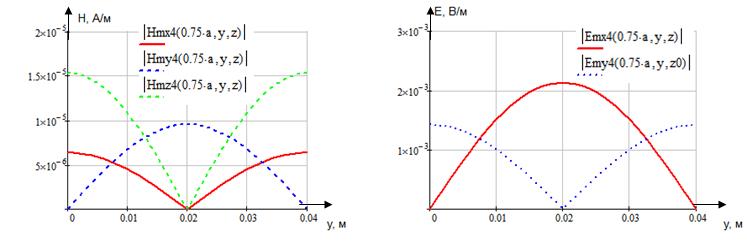
Рис. 8 Рис. 9
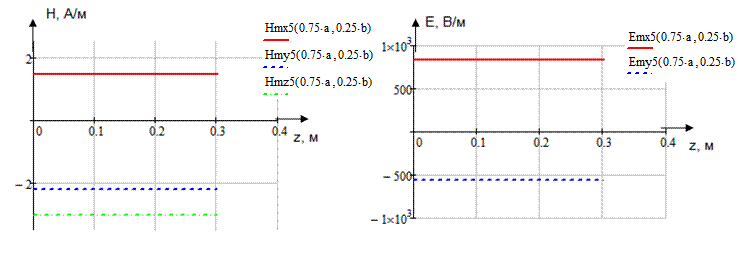
Рис. 10 Рис. 11
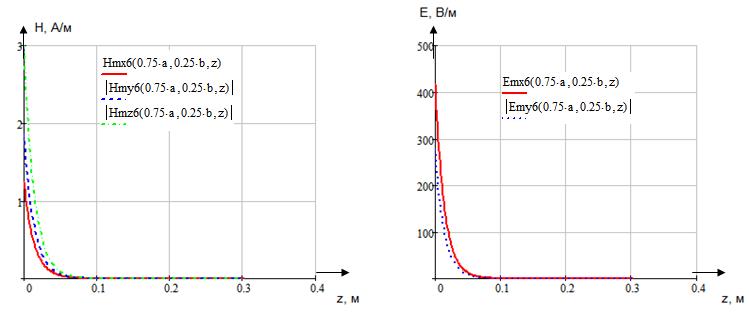
Рис. 12 Рис. 13
5)Проверка выполнения граничных условий для касательных составляющих вектора 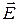 и нормальных составляющих вектора
и нормальных составляющих вектора 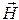 на боковой (х=а) стенке трубы.
на боковой (х=а) стенке трубы.
Как известно на границе раздела двух сред – идеального металла и воздуха 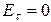 и
и 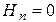 . Проверка граничных условий заключается в проверке истинности этих утверждений, т.е. равенства нулю касательной вектора
. Проверка граничных условий заключается в проверке истинности этих утверждений, т.е. равенства нулю касательной вектора 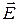 и нормальной вектора
и нормальной вектора 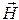 проекций (составляющих).
проекций (составляющих).
На боковой стенке (х=а) рассмотрению подлежат (17) и (13) составляющие:
Подставим в эти выражения х=а, получим:
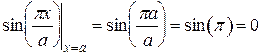 ,
,
При этом другие множители от координаты х не зависят. Следовательно, оба выражения обращаются в ноль и граничные условия выполняются.
Date: 2015-07-24; view: 4630; Нарушение авторских прав