
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Кеңістік квантталу. Электрон спині. Штерн-Герлах тəжірибесі
|
|
Затты сыртқы магнит өрісінде зерттегенде, атомдар мен молекулалардың магнит моменттері болатындығы байқалды. Бұл атомдарда магниттік əсерлесу болатынын жəне атом ішіндегі электрондарда да магниттік əсерлесулер болатынын көрсетеді.
Штерн-Герлах тəжірибесінде атомның жəне электронның магниттік моменттері бар екендігін дəлелдеді. Олар тəжірибеде күміс атомдарының шоғын біртекті емес магнит өрісінен өткізу арқылы зерттеді. Осыған қысқаша тоқталайық.
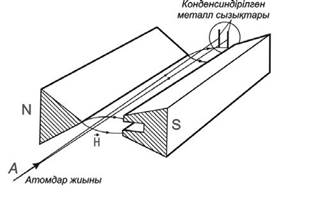
3.3-сурет
Пеш саңылауынан шыққан атомдар шоғын вакуум түтігінің ішіндегі магнит полюстерінен (N жəне S) өткізгенде (3.3-сурет), атомның магниттік моменті болса, оған сыртқы магнит өрісі бағыты бойынша бұруға тырысатын күш əсер етеді. Егер өріс біртекті болмаса, онда əрбір атомға ығыстырушы күш əсер етеді, ол
| х | (3.4.1) | |
~ 86 ~
| мұндағы, | – өріс градиенті, ол өрістің х-бағытында біртекті | ||
| емес | екендігін сипаттайды. | ||
| Н/ х |
- магниттік моменттің х-осіне түсірілген проекциясы. Егер, атомдардың магниттік моменттерінің бағыттары өрістің бағытымен салыстырғанда əртүрлі болса, онда əрбір атом түрліше ығысады. Штерн-Герлах осылай біртекті емес магнит өрісінен сутегі атомдарының күмістің, сілтілік металдардың шоқтарын өткізгенде, олардың шоқтарының əрқайсысы екі шоққа жіктелетіндігі байқалды.
Штерн-Герлах тəжірибесінде атомның магниттік моменттерінің бағыттары өріспен бағыттас не оған қарама-қарсы болуға тиісті. Сонда ғана атомдардың шоғына сыртқы магнит өрісі əсер етіп, екіге жіктеледі. Штерн-Герлах тəжірибесінің нəтижесінде алынған атомның магниттік моменті мынадай екі себептен пайда болады:
1) электрондардың орбита бойымен қозғалуынан. Классикалық электродинамика тұрғысынан қарағанда тұйық
орбита бойымен қозғалған электрон, тұйық сыммен жүрген электр тогына ұқсас, оның магниттік моменті болады. Осылай ядроны айнала қозғалған электронның орбиталдық магниттік моментінің шамасы (μl), электронның орбиталық импульс моментіне пропорционал. СИ-жүйесінде бұл мынаған тең:
| е | (3.4.2) | ||||||||||||||
| мұндағы: μ | – вакуумдегі | магниттік | өтімділік | 1,257· | |||||||||||
| 10 гн/м;Р 0 | - орбиталдық импульс моменті, ол | ||||||||||||||
| (3.4.3) | |||||||||||||||
| Ал, кванттық теория бойынша | |||||||||||||||
| (3.4.4) | |||||||||||||||
| (3.4.3) →(3.4.2) теңдеуіне апарып қойсақ, онда | |||||||||||||||
| · | Б | Б · | (3.4.5) | ||||||||||||

 ~ 87 ~
~ 87 ~
мұндағы Б- Бор магнетоны деп аталады. Б =1,15·10-29в.с.м. l=0;1;2;3;.....(n-1) мəндерге ие болады.
Егер сыртқы магнит өрісінің əсерінен, электронның магниттік моменттері, дискрет мəнге ие болса, мұндай құбылысты кеңістіктік квантталу деп атаймыз.
2) Электрон тек орбита бойымен ғана қозғалып қоймайды, сонымен қатар өзінің меншікті осінен де айналады, сондықтанда электронның меншікті магниттік моменті (μS)-болады, ол спиндік магниттік моменті деп аталады. Атом ішіндегі электронның меншікті импульс моменті мен спиндік магниттік моменті өзара байланысты. Тəжірибе нəтижелеріне қарағанда бұл екеуінің
| байланысы мынадай болады: | |||||||||||
| (3.4.6) | |||||||||||
| мұндағы, S – спиндік кванттық сан; | Б | тең, онда | |||||||||
| (3.4.7) | |||||||||||
Олай болса электронның спиндік магниттік моменті жуықтап алғанда Бордың бір магнетонына тең болады. Кванттық механикада электронның спиндік импульс моменті
1 (3.4.8)


Бұл электронның меншікті импульс моменті. Осы (3.4.8) формуланы (3.4.6) формулаға қойсақ, онда
| мұндағы, | √ | Б√ | (3.4.9) | |||||||||||
| в.с.м. болады. | ||||||||||||||
| Магнит | өрісінің бағытына түсірілген, электронның меншікті | |||||||||||||
| 1,99·10 |


 импульс моментінің проекциясы:
импульс моментінің проекциясы:
(3.4.10)

мұндағы: mS – спиндік магниттік кванттық сан.
~ 88 ~
Кванттық механика бойынша электронның орбиталдық импульс моментімен спиндік импульс моменттерінің геометриялық қосындысы электронның толық импульс моментін береді:
P l S l S 1 (3.4.11)


егер l±S=j деп алсақ
P j j 1 j (3.4.12)



мұндағы, j – ішкі кванттық сан.
Электронның толық магниттік моменті, электронның орбиталдық жəне спиндік магниттік моменттерінің векторлық қосындысына тең:
(3.4.13)
Сонымен атомның магниттік қасиеттері оның құрамындағы электрондардың магниттік моменттерімен сипатталады.
Егер атомның электрондары бірнеше болса, онда оның магниттік əсерлесулерінің жеке магниттік моменттері жинақталып қорытқы моментті береді. Онда əртүрлі типті əсерлесулер пайда болады: а) бірінші типтегі магниттік нормаль байланыс немесе L-S байланыс орындалады, яғни орбиталдық моменттерін жеке, спиндік моменттерін жеке жинақтап қосып, атомның қорытқы моменттерін табамыз:
∑; ∑;
µJ µL µS (3.4.14)
б) екінші əсерлесу типі
J-байланыс, мұнда жеке электрондардың орбиталдық жəне спиндік моменттерін өзара байланыстырып жалпы моментін (J) жəне жеке электронның толық моментін тауып, оларды қосып атомның толық моментін (J) табамыз:
~ 89 ~
| ; | ; | ; | |||
| j ∑ i | s | ∑ | |||
| ℓ | li | ∑ i | |||
| мұндағы: – атомның орбиталды моменті; | – атомның спиндік |
моменті; – атомның толық моменті. Сонда кванттық теория бойынша
| (3.4.15) | ||||||||
| (3.4.16) | ||||||||
| (3.4.17) | ||||||||
      ; ;
| жəне моменттердің квантталуының элементар ережесі, | |||||||
| атомның | векторлық моделінің сəйкестенуі мынадай түрде | |||||||
| жазылады: | ; | |||||||
| ; | (3.4.18) | |||||||
| Онда əсерлесу энергиясы да L,S,J – сандарының функциясы | ||||||||
| болады, ол жалпы түрде мынадай түрде жазылады: | ||||||||
| Е , | ,,;,, | (3.4.19) | ||||||
Бұл өрнек берілген L жəне S сандарының мəндеріне J-дің сан мəні байланысты болады: L+ S; L+ S-1; L+S-2... L-S+1; L - S; Бұл санның толық мəні: егер L> S болса, М=2S+1 мəні болады, егер L<S болса, онда М=2L+1мəнге ие болады.
М-саны деңгейшелердің санын анықтайды, спинге байланысты орбиталдық магниттік əсерлесу, ол мультиплеттік
энергия деңгейі деп аталады. Егер болса, М=2 дублет деп,

егер S=1 болса, онда М=3 - бұл триплет деп, ал S=0 болса М=1 сингулет деп аталады. Мультиплеттікті екі валентті атомдардан (гелий, берилий, магний) алынады.
Өте күрделі атомдардан бұдан да бай мультиплеттік алынады.
~ 90 ~
Date: 2015-07-24; view: 2374; Нарушение авторских прав