Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Сызықты гармониялық осциллятор жəне оның энергиясының квантталуы

⇐ ПредыдущаяСтр 23 из 106Следующая ⇒

 

Х осінің бойындағы, массасы m бөлшекке, f=-kx квазисерпімді күш əсер етсін, мұндағы k-серіппенің қатаңдығы, х-тепе-теңдіктен ауытқу шамасы. Ондай бөлшек барлық уақытта бастапқы тепе-теңдік қалпына қарай ұмтылады. Осындай тербелмелі жүйе сызықты гармониялық осциллятор деп аталады. Осылайша электр өрісінің əсерінен тербеліске келген электронды да сызықты гармониялық осциллятор деп қарастыруға болады. Электронға өріс тарапынан əсер ететін күш, оның тепе-теңдік қалпынан ауытқуының бірінші дəрежесіне (х) пропорционал болу керек, сонда ғана сызықты гармониялық осциллятор деп қарастыра аламыз.

 

Бөлшекке квазисерпімді күш х-координаты бағытымен əсер етсе, онда

fkx (3.3.1)

 

мұндай бөлшектің потенциалдық энергиясы

 

U kx 2  
  (3.3.2)  
     

Классикалық гармониялық осциллятордың меншікті жилігін ω0, қатаңдық (k) коэффициенті арқылы тауып, оны (3.3.2) формулаға қойсақ, онда

 

0 k / m (3.3.3)  
k m 02 U m 2 x 2 (3.3.4)  
   
         

олай болса гармониялық осциллятор үшін Шредингер теңдеуін мынадай түрде жазамыз.

2           2 2      
d   2 m m x   (3.3.5)  
E      
dx                    
               

немесе

 

~ 84 ~


2 8 2 m (E m 2 x 2 ) 0;

2 2

 

мұндағы, Е - осциллятордың толық энергиясы. Бұл теңдеу арқылы энергияның (Еn) дискретті мəндерін анықталады:

  n 1   (3.3.6)  
En   0 n=0,1,2…  
         

мұндағы, n – тербелмелі кванттық сан деп аталады.

 

Сонымен осциллятордың толқындық теңдеуін қанағаттандыратын Ψ функциясы, осциллятор энергиясының дискреттік мəнін қанағаттандырады. (3.3.6) формуладағы сызықты гармониялық осциллятордың кванттық саны əр кезде

  n 1    
«жартылай бүтін» кванттық санмен сиппатталады   .  
       

Егер n=0 болса да, осциллятор энергиясы нөлге айналмайды:

 

E 0 1 0 (3.3.7)  
   
       

Бұл (3.3.7) теңдеу «нөлдік энергия» деп аталады.

 

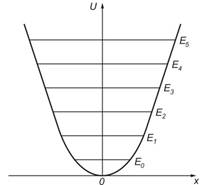
3.2-сурет

 

Бұлай аталу себебі температура абсолют нөлге тең болса да, энергия нөлге теңелмейді (3.2-суреттегідей). Яғни, температура абсолют нөл болған күйдің өзінде де осциллятор тербелісте болады да, ол кесіндінің кез келген бөлігінде немесе кесінді

 

~ 85 ~


сыртында да кездесу ықтималдығы болады, оның амплитуда-сынан екі еселенген мəнге үлкен болады.

 


⇐ Предыдущая18192021222324252627Следующая ⇒





Date: 2015-07-24; view: 1306; Нарушение авторских прав


mydocx.ru - 2015-2024 year. (0.006 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию