Главная Случайная страница


Полезное:

Как сделать разговор полезным и приятным Как сделать объемную звезду своими руками Как сделать то, что делать не хочется? Как сделать погремушку Как сделать так чтобы женщины сами знакомились с вами Как сделать идею коммерческой Как сделать хорошую растяжку ног? Как сделать наш разум здоровым? Как сделать, чтобы люди обманывали меньше Вопрос 4. Как сделать так, чтобы вас уважали и ценили? Как сделать лучше себе и другим людям Как сделать свидание интересным?


Категории:

АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника






Потенциалдық шұңқырдағы бөлшек

⇐ ПредыдущаяСтр 22 из 106Следующая ⇒

 

Шексіз терең потенциалдық шұңқырдағы микробөлшекті қарастырсақ ол мына түрде сипатталады: егер бөлшек (0,а) аралығында болса, оның энергиясы тұрақты нөлге тең (3.1а-сурет).

 

~ 80 ~


 

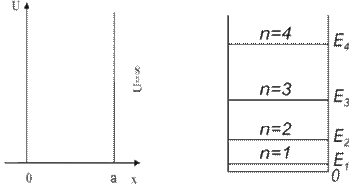
а) б)

 

3.1-сурет

 

Шекараға жақындағанда оған шексіз үлкен кері итеру күш əсер етіп, бөлшек шұңқыр қабырғасынан кері

 

шағылады. Осы жағдайда бөлшек (0,а) аралығынан шыға алмайды.

 

Ондай бөлшектің күйін анықтау үшін бір өлшемді Шредингер теңдеуін шешу керек. Осы мақсатта Шредингер теңдеуін х-осі бойымен бір өлшемді қозғалыс үшін жазайық:

2        
d   2 m (E U)0; (3.2.1)
dx 2        

Бұл жердегі сыртқы потенциалдық өріс төмендегідей болсын:

 

∞,онда x 0 І облыс үшін

 

0,онда 0 x ІІ облыс үшін (3.2.2) ∞,онда x a ІІІ облыс үшін

Мұндай өріс шексіз терең потенциал шұңқыр деп аталады. Бөлшек шұңқырдың шекарасына жақындағанда оған шексіз үлкен кері итеруші күш əсер етеді:

 

F x dU   x 0, a   (3.2.3)  
   
dx    
           

~ 81 ~


Сондықтан бөлшек шұңқыр сыртына шыға алмайды. Олай болса, шұңқырдан тысқары нүктелерде толқындық функция нөлге тең болғандықтан, толқындық функция үздіксіз болу үшін, шекаралық нүктелерде функция нөлге тең болуы керек.

 

(0)(a) 0 (3.2.4)

 

Бұл формуланы шекаралық шарт ретінде аламыз. Оның, физикалық мағынасы бар ол (3.2.1) формуланың шешуін қанағаттандыру керек.

 

Потенциалдық шұңқыр ішінде 0 болса, онда U =0 болғандықтан, (3.2.1) теңдеу мынадай түрге келеді:

                  2 m          
            d       (3.2.5)  
            dx 2       2 E 0;    
                     
      2 m                 2 k      
        d              
k       E   k 0 E     (3.2.6)  
  2 dx 2 2 m    
          x c sin kx      
                                 

Бұл теңдеудің дербес шешімі шекаралық шарт (3.2.4)-ті қанағаттандыру үшін Сsin (k) = 0; k =nπ; (n=1,2...)

 

Бұдан толқындық санның кез келген мəндерді қабылдай алатынын көреміз. Оның шамасы шұңқыр ішіне жарты толқын ұзындығы бүтін сан ретінде орналасатындай болу керек. Бұдан

мынадай квантталу шартын аламыз:;

n x C sin ax n

  ћ     ћ           (3.2.7)  
Энергияның меншікті мəнін табу үшін, (3.2.5) формуладағы  
2mE/ коэффициентін d 2 - коэффициентімен алмастырсақ, онда  
        0;    
  dt 2       (3.2.8)  
                 
λ   k n         2 a  
        n   (3.2.9  
      n  
           

~ 82 ~



онда

 

d           n      
        ;    
            (3.2.10)  
dx 2      
        2 a      

 

(3.2.5) жəне (3.2.10) теңдеулерді теңестіріп:

 

2 m       n      
E n 4      
               
           
        2 a    

Бұдан энергияны тапсақ, ол

 

E n   2 n 2   n= 1,2,3... (3.2.11)  
  2 ma 2    

Бұл теңдеу (3.2.11) бөлшектердің квантталу энергиясының меншікті мəні болып табылады. Демек энергия дискретті мəндер жиынтығын қабылдайды.

 

Потенциалдық шұңқырдағы бөлшектің квантталу энергиясын шекаралық шарттарды қолдану арқылы анықтай аламыз (х=0, x=a). Шұңқыр ішінде бөлшектің потенциалдық энергиясы болатындықтан, толық энергия кинетикалық энергияға тең болады. Бөлшек энергиясы квантталған, яғни бөлшек энергиясы тек белгілі дискреттік мəндер қабылдай алады, бұлар меншікті

 

мəндер болады. En деңгейге сəйкес келетін n бүтін сан, ол

 

деңгейдің кванттық саны деп аталады. 3.1.б-суретте бөлшектің бірнеше энергия деңгейлерінің орналасуы көрсетілген. Энергияның ең аз мəніне негізгі күй, ал қалған мəндеріне қозған күйлер сəйкес келеді.

Екі көршілес деңгейдегі энергиялар айырымы, n үлкен сан болғанда:

 

En En 1 En         2 n           n (3.2.12)  
         
     
2 ma 2 2 ma 2  
Яғни, энергия айырымы (En) бөлшек массасы (m) жəне  

шұңқыр ені (а) кеміген сайын арта түседі.

 

Шұңқырдағы бөлшектің энергиясы нөлге тең болуы мүмкін емес. Егер бөлшек энергиясы нөлге тең болса, онда толқындық функциясы да шұңқырдың кез келген нүктесінде нөл болар еді. Онда бөлшектің шұңқырда болуы мүмкін емес. Бөлшек энергиясының нөлге тең болуы жəне мүмкін мəндерінің белгілі


 

~ 83 ~


дискретті мəндермен шектелуі кванттық механикаға тəн нəтижелер. Классикалық механикада энергия кез келген мəнге, соның ішінде нөлге де тең болады.

 


⇐ Предыдущая17181920212223242526Следующая ⇒





Date: 2015-07-24; view: 2353; Нарушение авторских прав


mydocx.ru - 2015-2024 year. (0.014 sec.) Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав - Пожаловаться на публикацию